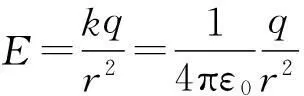带电体的电势及场强求解方法

黄开智

(江苏省姜堰二中，江苏　泰州　225500)

带电体的电势及场强求解方法

黄开智

(江苏省姜堰二中，江苏泰州225500)

摘要：本文探讨了均匀带电球体和球壳周围的电势及电场强度分布情况，并通过Mathematica软件模拟了等量异种电荷电势的三维分布，总结了几种典型的带电体的电势及其场强的计算方法.

关键词：电势；电场强度；高斯定理；Mathematica软件

在电磁学的习题中常会遇到求解带电体模型的电势或者场强的问题，例如均匀带电球壳、均匀带电球体、等量异种或同种点电荷等模型.高中阶段，学生很难分清楚电势与电场强度的概念及其计算方法，仅能勉强求解一些比较特殊点的电势或者电场强度.经验不足的教师也不大清楚典型带电体周围电势的变化情况，导致不能站在一个更高的角度来施教.

静电场中某点的电势在数值上等于单位正电荷在该点处的电势能，也等于单位正电荷从该点经过任意路径移到无限远处时电场力所做的功(此时认为无穷远处电势为零).若已知电荷在空间的分布，一般来说求电势或场强的方法有两种，可根据不同电荷分布，选择不同方法：一种是先求解出电场强度E的分布函数，应用场强与电势的关系，对场强做线积分运算，求解电势；另一种是直接根据电势叠加原理，求解任意点的电势，进而运用电势梯度的负值等于场强的特点求解该点场强.

1均匀带电球体的场强及电势分布

问题：均匀带正电球体置于真空中，带电量为Q，球体半径为R，球心为O，求球体周围空间的电场强度及电势.

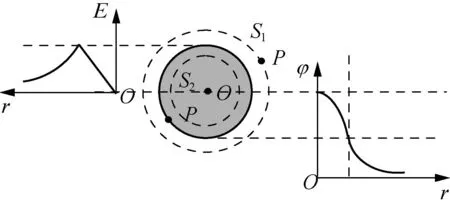
图1

分析：如图1所示，由于球体具有球对称性，因此在三维空间我们可以选取球坐标(r、θ、φ)来研究电场强度.在r>R的空间，可以将球体看成点电荷模型处理.在r

解：(1) 通过以上分析可得到的结论是：任一同心球面上场强大小E都相等，方向与此球面垂直.接下来需要利用静电场的高斯定理来计算场强的大小.

图2

图2给出了该种带电球体电场强度的函数分布图.可以看出，均匀带电体的场强是连续的，且在球体表面处场强有极大值.

图2也给出了该种带电体电势的函数分布图，不难看出，均匀带电球体周围的电势和电场一样也是连续的，且电势在球心处有最大值.

这里要说明两点：其一，由于均匀带电体不是一个稳定状态，电荷最终会向带电体表面移动，形成一个带电面，尤其是导体，此时场强或电势分布将会出现变化(本文第2部分将会说明).其二，若是针对均匀带电体，按照高斯定理，体内的场强就不会是零，这点很容易与处于静电平衡的带电体内场强为零的结论相混淆.

2均匀带电球壳的场强及电势分布

问题：均匀带正电球壳置于真空中，带电量为Q，球壳半径为R，球心为O，求球壳周围空间的电场强度及电势.

分析：如图3所示，带电体为球壳，相比带电球体，其选用的坐标系和理论方法同出一辙，但场强的计算要简单得多.在处理这个问题时，同样分r>R和r

图3

若P点在球内(图3中高斯面S2)，此时发现，任一高斯面内均没有电荷，故在球壳内部任一点的场强E=0.

(2) 选择无穷远点为电势的参考位置.

对比带电球体和球壳，不难看出，各自的场强和电势分布有很大不一样.首先，对于场强而言，前者是连续的，极大值出现在球体表面处，而后者则是跳跃的，且球壳内部场强处处为零，类似静电平衡的导体；其次，对电势而言，前者电势一直在降低，后者在球壳内部的电势不变，为一等势体.

3等量异种电荷的场强及电势分布

图4

图4给出了真空中等量异种电荷模型，两电荷各自带电量为q，相距l，O为电荷连线中点.求与电荷模型距离较远的P点的电势和场强分布.

图5

图6

4场强及电势分布一般处理方法

通过以上计算及相关模拟，在求解带电体的电势或场强时，二者是等价的.如果带电体的场强相对说来比较好求解，可以先求解场强，进而求解电势，而这种带电体多为单个带电体，且几何形状比较规则；假若带电体为多个，一般是先求解电势，之后求解场强，因为电势的求解就是普通的标量叠加，相比场强的矢量叠加来说较为简单.

参考文献：

[1] 赵凯华，陈熙谋.电磁学 [M]. 北京：高等教育出版社，2006 ：20-24.

[2] 中学物理教师手册编写组.中学物理教师手册(下册)[M]. 上海：上海教育出版社，1983 ：470-472.