压力容器材料断裂韧性值的估算方法

严 进

（西安石油大学机械工程学院，陕西 西安 710065）

压力容器是在石油化工行业使用中可能引起易燃易爆或中毒等事故的特种设备之一。含有缺陷的压力容器设备是否可以继续安全使用关系到设备运行的安全性和经济性，因此需要对含缺陷的压力容器设备进行科学的安全评定。通常研究含缺陷压力容器的断裂规律及安全评定时，材料的断裂韧性KIC值和裂纹尖端应力强度因子KI值是评定含缺陷压力容器设备是否能够继续安全使用的主要参数。而材料的断裂韧性是材料的物理属性，通过实验测量，寻找出材料断裂韧性与常规力学性能之间的关系就显得非常有必要。利用KIC估算公式，既能减少断裂韧性试验的费用，又能取得评价所需要的参数值。

1 GB 19624-2004中压力管道材料断裂韧性值的简化估算

KIC反映材料抵抗裂纹失稳扩展的能力，是材料的力学性能指标。它是材料强度和韧性的综合反应，与裂纹本身的大小、形状、外加应力等无关，主要取决于材料的成分、内部组织和结构。材料的断裂韧性值是通过实验获得的，在不能用标准方法进行断裂韧性测试时，根据国标[1]可以通过公式（1）、（2）估算。

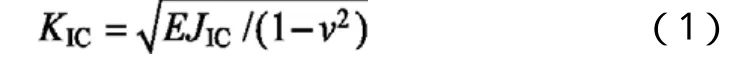
式中：E为材料弹性模量；JIC为弹塑性断裂韧度；σS为材料的屈服强度，v为材料的泊松比。

评定时若没有给出材料的JIC值就用材料断裂韧度的下限值，（JIC）下限可取1.14AKV，对未焊透缺陷可取2.2AKV，也可以根据评定人员过去使用该种材料的历史经验决定。如果评定时缺乏材料的AKV数据，若评定人员能判断材料适用于压力容器，且在使用状态下无脆化倾向，使用温度不低于材料的转变温度，在评定时可以取压力容器材料容许的最低值AKV=27J。此方法在未知压力容器材料断裂韧性值的情况下，能够简单便捷地评定出压力容器的安全性，但其评定方法过于保守，未能达到充分地安全使用设备的目的。

2 CTOD法估算断裂韧性值

裂纹尖端张开位移(CTOD)法是测试金属材料断裂韧性的主要方法之一。在平面应变状态下, 根据线弹性断裂力学, 金属材料的断裂韧性值可以依据公式（3）计算[2-3]。

式中：mCTOD为转换常数，取值1.4；σf为流变应力，，MPa；σv为材料屈服强度，MPa；σu为材料抗拉强度，MPa；δrit为极限CTOD值，mm；Eν为弹性模量，取值2.06×105MPa；ν为泊松比，取值0.3。

美国石油协会出版社的管道适应性评价规范提出，金属材料的断裂韧性KIC可以利用夏比冲击功CVN，采用公式（4）估算。

骆建武等[4]从国内外4家钢管厂选取X80级钢作为CTOD试验用材料，依据GB/T 2358-1994《金属材料裂纹尖端张开位移试验方法》进行试验，CTOD数据取裂纹扩展量为0.2mm时的值，即δ0.2按公式（3）计算钢管的断裂韧性值，并且以此值作为断裂韧性的试验观测值，同时按照ASIME 23-2005的试验方法，测定各个试样的冲击功，利用公式（4）计算材料的断裂韧性值，并与试验观测值比较发现，用CVN法估算的X80级钢的断裂韧性值与试验观测值偏差较大，且CVN法估算值全部小于试验观测值。骆建武等又利用回归模型建立了X80级钢夏比冲击功与其断裂韧性之间的经验关系式，将夏比冲击功作为随机变量处理，断裂韧性作为因变量处理，得到经验公式（5）。

此经验公式计算的断裂韧性值与样本数据是高度相关的，与API 579-2007推荐的公式对比表明，此公式可以对X80级钢的断裂韧性做出更准确的估算。利用此公式可以估算出X80级钢 的断裂韧性值，对评定其安全性提供了方便。但是此经验公式是依据裂纹张开位移计算出的断裂韧性值作为试验观测值拟合的，而不是直接依据试验测得的断裂韧性值进行拟合的，所以虽然拟合的经验公式与样本数据高度相关，但还是存在间接误差，如果能直接依据测得的断裂韧性值进行公式拟合，则拟合的经验公式对断裂韧性值的估算更为准确。

3 压力容器在中温工作环境中材料的断裂韧性值的估算

当压力容器设备在温度较高介质中运行时，随着温度的升高，材料的断裂韧性会出现下降趋势。对于压力容器在中温范围内的断裂韧性行为，Matsuzawa等[5]对多种压力容器材料进行了实验研究，发现随着温度的升高，断裂韧性出现下降的趋势。EricksonKirk[6]从流变应力方面考虑，建立了中温断裂韧性与温度的关系，且在ASTM STP-1360中从微观机制方面提到了关于中温断裂韧性的变化规律。文献[7]关于中温断裂韧度的研究等均表明，随着温度的升高，断裂韧性出现下降的现象。

近年来，材料损伤断裂行为的研究进入了宏微观相结合的理论阶段，考虑材料的微观组织结构，引入多层次的缺陷几何，追溯材料从变形、损伤到断裂的全过程。李余德等[8]提出的塑性断裂模型以及点缺陷在应力场中的迁移运动规律，从空位浓度方面研究，通过一些分析和假定建立了1型裂纹中温范围内断裂韧性JIC和温度T的关系为：

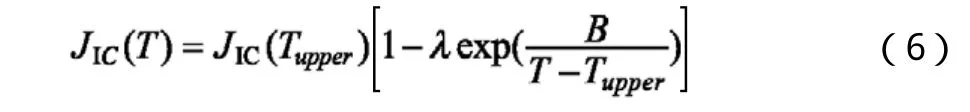
JIC(Tupper)为材料上平台温度的断裂韧性，B= -Ef/k，为空位浓度中的空位形成能项对断裂韧度对比系数的影响，且B＜0；Ef为空位形成能，可由实验测得；k为玻尔兹曼常数。λ=μα0，为空位浓度中的振动熵项对断裂韧度对比系数的影响；α0=exp(Sf/k)，是材料在特征温度下由振动熵Sf决定的系数，μ为比例系数，且μ＞0。同时李余德等同国际同行EricksonKirk进行交流，获得了多种压力容器钢中温断裂韧性的实验数据，采用提出的断裂韧性关系式进行了曲线回归分析，提供了一种理论计算1型裂纹断裂韧性值，并一共对38种试样做了分析。结果表明，公式进行线性回归分析得到的各种试样在不同温度下的断裂韧性值与实验结果吻合得很好，此公式能够估算出各种钢在中温环 境中1型裂纹的断裂韧性值，对于评定中温环境下的缺陷压力容器设备提供了方便。只是对于估算的裂纹类型过于单一，只能估算1型裂纹的断裂韧性值，如果再能估算出其他类型裂纹的断裂韧性值，则公式就能更为广泛应用。

4 应力腐蚀临界强度因子KISSC值的简化估算

含裂的压力容器设备在腐蚀介质中运行时，在受载相同的条件下, 由于裂纹尖端存在电化学腐蚀，使裂纹加速扩展，致使设备在所受应力σ小于其临界应力σc时，即能发生应力腐蚀断裂。假设裂纹从原始尺寸2α0扩展到临界尺寸2αC所需的时间为t，裂纹在腐蚀介质作用下，当应力强度因子KI＜KIC时，裂纹扩展所需的时间t会随KI的下降而增大，即应力强度因子越小，设备使用的寿命就越长。当应力强度因子KI下降到某一临界值时，设备使用寿命足够长，该临界值即为应力腐蚀临界强度因子KISSC。因此，对压力容器等含缺陷构件的应力腐蚀脆断进行安全评定时，其失效判据即为KI≤KISSC，对于特定的金属材料和特定的腐蚀介质而言，其应力腐蚀的门槛值KISSC必定为定值。

在工程实际应用中，材料的应力腐蚀强度因子门槛值KISSC是通过特定的实验装置利用恒定载荷法或恒定位移法测得的。但鉴于应力腐蚀断裂涉及到大量不同的金属材料和腐蚀介质，采用实验测定方法获取KISSC值有一定的困难，即难以测得任何一种介质环境下的应力腐蚀临界强度因子KISSC值。因此，有必要寻求一种简单直接的KISSC工程计算方法。

许多针对应力腐蚀临界强度因子KISSC的研究均表明[9-11],材料的屈服应力σS是对KISSC敏感的一个重要影响因素。以此为基础, Gerberich[12]导出了σS与KISSC之间的关系为：

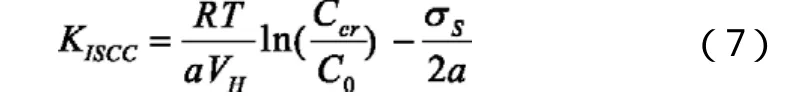
式中：R为气体常数，即R=8.3×10-6MN·m·(mol·k)-1；T 为绝对温度，K；a 为常数，即 13m1/2；VH为氢气在钢中的偏克分子体积，即2×10-6m3·mol-1；σS为材料的屈服点；C0、Ccr分别为起始氢的平均浓度和临界浓度。

在后来的研究中, Kim-Loginow[13]认为，氢易于溶入高强度钢，C0与σS成正比，从而可以近似代替Ccr/C0，导出了如下估算公式：

式中：β为材料常数。研究表明，对于含碳量为0.4%左右的钢材, 用式（8）计算所得的KISSC值与实测值比较符合。当含碳量有较大变化时，则误差较大。为此，陈南平等[14-15]对式（8）进行了修正，即用(A+B/C)代替Ccr/C0值，并考虑了含碳量变化及水介质中应力腐蚀断裂方式的影响, 得出式（9）：

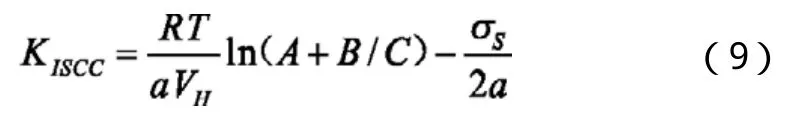
式中：C为钢材的含碳量，%；A、B为裂纹断口形貌决定的常数。

对于含碳量为0.1%~0.4%的各种低合金钢，胡兆吉等[16]利用式（9）计算得出的KISSC值与实验所测值比较，结果均能很好地吻合。有了KISSC的工程计算方法，即可以很方便地应用应力腐蚀条件下的强度判据即KI＜KISSC，对压力容器等含缺陷构件在应力腐蚀条件下的裂纹扩展状态进行安全评定。公式（9）给出了腐蚀环境下的断裂韧性值的估算方法，可以很好地估算含碳量为0.1%~0.4%的各种低合金钢的断裂韧性值，不足之处就是不能估算出高合金钢材料在腐蚀环境中的断裂韧性值，因此在这方面还需进一步的深入研究。

5 总结

研究含缺陷压力管道在静力、变力载荷作用下的线弹性断裂规律及安全评定时，在不考虑其周围工作环境的影响时，认为裂纹构件在载荷作用下，只要控制裂纹尖端应力强度因子KI值小于材料的临界应力强度因子KIC（即材料的断裂韧性）值，即控制裂纹尖端的应力σ小于材料的临界应力σC,构件即是安全的，所以估算出材料的断裂韧性值即可评定出缺陷管道的安全性。当构件处于高温高腐蚀环境工作时，即使KI＜KIC,通常也会产生断裂破坏而使管道失效。工程经验和研究结果表明，材料在其工作温度范围内，其断裂韧度值在上平台温度以上会随着温度的升高而下降即存在韧性劣化现象，因此估算其断裂韧性值时应估算其在工作温度环境下的断裂韧性值。对于腐蚀介质环境，其介质腐蚀作用加快了含缺陷压力容器的裂纹扩展速度，导致压力容器更早地发生应力腐蚀断裂，估算断裂韧度值时应估算其在腐蚀介质中的应力强度因子临界值KISSC。本文推荐了几种环境下缺陷压力容器的断裂韧性值估算方法，避免了利用试验获得的断裂韧性值的困难，但是没有说明其估算方法在工程实际应用中的适应性。在进行安全评定时，建议尽量采用实验测定值，对于特定材料和特定介质，当无法实验测定时采用估算方法进行计算求得。

[1] GB/T 19624-2004，在用含缺陷压力容器安全评定[S].

[2] 周惠久，黄明志.金属材料强度学[M].北京：科学出版社，1989.

[3] API 579-2007. Fitness-For-Service[S].

[4] 骆建武，覃海涛.高钢级管线钢断裂韧性确定方法研究[J].焊管，2009(7)：33-37.

[5] Matsuzawa. H, Osaki T. Fracture toughness of highly irradiated pressure vessel steels in the upper shelf temperature[C].Vancouver(Canada): ASME Pressure Vessels and Piping Division, 2006.

[6] EricksonKirk Mark, EricksonKirk Marjorie. An upper shelf fracture toughness master curve for ferritic steels[J]. International Journal of Pressure Vessels and Piping, 2006, 83(8): 571-583.

[7] Li Yude. An explanation of the relationship of fracture toughness to temperature in the range from upper shelf to first phase transformation[J]. Engineering Fracture Mechanics, 1992, 43(2): 305-311.

[8] 张志明，李余德，牛延军，等.材料断裂韧度随温度变化的研究[J].力学与实践，2010(6)：43-48.

[9] 任凌波，任晓蕾.压力容器腐蚀与控制[M].北京：化学工业出版社，2003.

[10] 李志安，金志浩，宮尖端.压力容器断裂理论与缺陷评定[M].大连：大连理工大学出版社，1994.

[11] 陈学东，蒋家羚，等.湿H2S环境下典型压力容器用钢应力腐蚀开裂门槛值的估算[J].压力容器，2004，21(3)：1.

[12] Gerberich W W, Garry J, Lessar J F. Ineds.Thompson A W, Bernstein I M. Effect of Hydrogen on Bebavior of Materials[C]. New York: AIME, 1976.

[13] 肖纪美.不锈钢的金属学问题[M].北京：冶金工业出版社，1983.

[14] 中国机械工程学会材料学会.脆断失效分析[M].北京：机械工业出版社，1993.

[15] 陈南平，顾守仁，沈万慈.机械零件失效分析[M].北京：清华大学出版社，1988.

[16] 胡兆吉，卢黎明，邓腾，谢志刚.含缺陷压力管道的应力腐蚀断裂及其安全评定[J].腐蚀科学与防护技术，2006，18(1)：76-78.