页岩气吸附模型的研究进展
2015-01-29姚逸风张雪飞彭孟春
江 楠,姚逸风,徐 驰,张雪飞,彭孟春
(长江大学石油工程学院,湖北 武汉 430100)
页岩气在新能源领域资源潜力巨大,受到世界各国的广泛关注。我国各地质时期页岩分布广泛,资源十分丰富,总资源量可达100×1012m3,相当于常规天然气量的2倍,与美国的页岩气资源量大体相当。在能源状况日益紧张的情况下,开展对页岩气等非常规能源的研究,对改善我国能源结构,减少对常规能源的依赖性具有重要的意义[1]。就目前国内对页岩气开发的研究来看,主要针对的是钻井、储层评价和改造等与工艺密切相关的领域,而页岩气主要是以吸附气存在,对页岩气吸附模型方面研究较少,这会影响我国对页岩气的开发和利用[2]。
1 经典页岩气吸附模型研究
1.1 Langmuir模型的推导
Langmuir模型是法国化学家Langmuir 在1916年研究固体表面的吸附特性时,从动力学观点出发,提出的单分子层吸附的状态方程,适用于无孔固体。其基本假设条件为吸附剂表面均匀光洁,固体表面能量均一,仅形成单分子层,被吸附的气体分子之间没有相互作用力,吸附平衡时处于一种动态平衡。由于页岩吸附页岩气的等温线与单分子层的等温线形式相同,所以可运用Langmuir模型来计算吸附气含量[3]。
Langmuir方程表示的是一种理想吸附,理论假设吸附为单分子层吸附,各吸附位点能量均匀且被吸附的分子间无相互作用[4],Langmuir单分子层吸附模型推导如下:基于Gibbs吸附等温式,一个简单的模型是将吸附在界面上的吸附质视为单分子层的二维气体, 类似于Vander Waals流体,首先假定其服从如下二维状态方程:

式中A 是界面面积,N是被界面吸附的气体物质的量,a0和b0是方程的2个参数,其中a0为引力常数,表征已吸附气体分子间的相互作用大小,b0称为协面积,相当于1mol已吸附气体分子所占的面积,N/A即为单位界面的吸附量。
现将式(1)代入Gibbs吸附等温式:

经运算和整理,得到以下公式:

式中θ=b0为界面覆盖度,k0=2a0/(b0RT),K是一个正比于b0的常数。此式即为Hill-deBoer吸附等温式。它的一个重要特点是能描述气体分子在界面上凝聚成二维液体的现象,并预示二维气液转变的临界值。
倘若二维气体分子间的作用可以忽视, 即引力常数a=0,则状态方程变为:

相应的吸附等温式变为:

此式即为Volmer吸附等温式。它能很好地用来描述有机蒸气在汞表面上的吸附情况。本文要指出的是,这个单分子层二维气体模型还能近似或半经验地用来建立各种熟知的气固吸附等温式。对于式(4)不难理解,其中A/Nb0是未占的界面积,本文不妨称其为自由面积,并用Af表示之。于是,它亦可表示为:

现若假定Af=A/α,即自由面积正比于界面面积,这意味着界面覆盖度变化区间不是很大。则:

将它代入式(2),并积分可得:

令 C=ln k,则:

式中比例常数α=A/Af>1,这正是熟知的Freundlich吸附等温式,它适用于覆盖度变化不是很大的中等压力范围。
式(4)亦可表示为:

式中Am,f=Af/N,相当于摩尔自由面积。考虑到Am,f应随气相平衡压力而变,压力愈高, 因吸附愈多, Am,f则愈小。当p→∞时,因界面完全被气体覆盖,此时 Am,f→ 0;当 p→ 0时,因 N → 0,Am,f→∞。因此, 有理由认为Am,f与ln(1+bp)成反比,亦即:

式中A为比例系数,b是一个表征吸附强弱的特性参数。因为b值愈大,P愈大,亦即吸附使界面张力减少愈多,故吸附愈强。将式(11)代入式(2)可得:

由于p→∞时, Γ→ Γ∞, 且1+bp≈bp,故α=Γ∞。上式亦可写成:

这就是经典的Langmuir吸附等温式[5]。
1.2 Langmuir的局限性
虽然langmuir方程被广泛用于拟合页岩气吸附实验结果,但是langmuir方程只适用于中低压条件下(<15MPa)页岩气吸附实验的拟合,langmuir也难以体现页岩中干酪根和黏土矿物吸附能力的差异。张键等人[6]在对富县区页岩样品吸附实验数据拟合的过程中,发现langmuir模型对实验数据的适应性效果都不太好;张志英等人[7]对鄂尔多斯3个页岩岩样在不同温度、不同压力条件下,进行吸附实验数据拟合,发现langmuir方程的拟合效果不好,相关系数最大不到0.85。
2 页岩气吸附模型的发展
Langmuir理论是基于吸附质与吸附剂之间的相互作用而完全忽略吸附质分子之间相互作用,只对均一吸附剂表面的单分子层吸附有效,并不适用于多分子层吸附,除此之外,Langmuir模型适用的条件非常苛刻,一般需要达到以下条件:
1)吸附平衡时,体系中气体的吸附速度与脱附速度相等,吸附和脱附之间没有滞后发生;
2)吸附剂表面均匀光洁,固体表面的吸附势能呈均质状态,活化能为0kJ·mol-1;
3)被吸附的气体分子间没有相互作用力;
4)固体表面吸附平衡仅形成单分子层[8]。
正是因为这些苛刻的条件使得Langmuir模型在实际生产应用中受到了限制,因此后人对Langmuir模型进行了一定的修改和加工,从而创造出了E-L模型、双langmuir模型、BET模型[9]等等。
2.1 EL(Extended-Langmuir)模型
Extended-Langmuir模型如下:

式中,qi为混合气体中i组分的吸附量;qe,i为组分i 的平衡吸附量;ci为i 组分在气相中的分浓度(或分压)。
2.1.1 EL模型的优越性
1)该方程能够很好地关联吸附数据且方程形式也很简单。
2)当吸附多组分混合气体时,Langmuir方程失效而此方程仍可使用。
3)该方程可以计算出具体吸附剂对混合气体的总吸附量,而Langmuir方程则不能[10]。
2.2 双 Langmuir模型
设吸附质表面有n种类型的吸附点,Ni代表气体在第i种吸附质表面的吸附量,则气体总吸附量为各个吸附量的总和,即:

假设fi为第i种吸附质在单分子覆盖面Nmi上的吸附比例,则有:

式中,Nmi为第i种吸附质覆盖的表面积;Nm为单分子层的表面积;θi为第i种吸附质的相对吸附量,该值满足朗格缪尔吸附假设。
页岩中的黏土和干酪根(有机质)是影响气体吸附的主要因素,假设黏土和干酪根这两种物质为均一吸附质,综合上述两式,得到如下关系式:
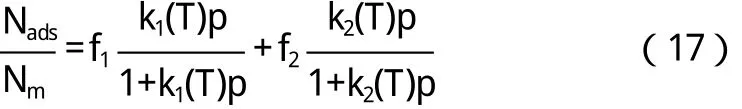
其中f1+f2=1。
将上式变形得:

该模型描述的是吸附质具有2种独立的能量分布的气体吸附模型。上式分两部分,一部分表示的是气体在黏土矿物质表面的吸附,另一部分表示的是气体在有机质表面的吸附。上述模型为双朗格缪尔吸附模型[11]。
2.2.1 双langmuir模型的优越性
1)对于黏土含量较大的页岩,双Langmuir模型比Langmuir模型更加适用。
2)对于非均质吸附质而言,双Langmuir模型比Langmuir模型拟合结果更加准确[12]。
2.3 BET模型
n层BET吸附模型为:

Γ∞为单分子层饱和吸附量,x=p/p*(一般不大于0.35时拟合效果较好)为吸附质的平衡压力与它在实验温度下的饱和蒸气压之比,c=exp((q1-qL)/(RT)),其中q1为第一层的吸附热,qL为其他各层的吸附热或凝聚热[13]。
2.3.1 BET模型的优越性
1)BET等温方程能确定催化表面 的最大值。
2)它适用于多层吸附,即物理吸附(吸附分子以类似于凝聚的物理过程与表面结合,即以弱的范德华力相互作用)的情形,它比Langmuir等温方程能更好地拟合实验数据。2.3.2 BET模型的缺陷
BET理论模型也有其自身的缺陷,它对大多数中孔吸附剂是有效的,对于小孔或者微孔等吸附剂则不理想[14]。
2.4 D-R(Dubinin-Radushkevich)模型
D-R 方程如下:

式中,n为1g吸附剂所吸附的吸附质的物质的量;n0为饱和吸附量,即微孔发生完全填充时的吸附量;P为吸附平衡压力值;P0为吸附质的饱和蒸气压;D为模型参数,满足D=(RT/E)2;E为特征吸附能。
2.4.1 D-R模型的优越性
1)形式相对复杂;2)功能多,可计算出吸附剂微孔体积、吸附容量和相关吸附热数据[15];3)预测结果准确。
2.4.2 D-R模型的缺陷
1)不能直接得到组分吸附量数据;2)涉及吸附质亲和力系数的计算;3)不适用于低压下和含有超临界组分的预测[16]。
3 结论与认识
经典模型如BET模型、D-R模型在拟合超临界状态的页岩气以及对多组分的拟合下都有各自的优越之处,同时在这些模型的实际拟合中也存在一些不足之处,例如有些模型计算过程复杂以及不适应某些状态下的拟合等[17]。
还有一些认识不清或未解决的问题,值得深入研究,总结如下:
1)页岩气的主体赋存状态存有争议,对固溶态的页岩气的研究还很少。
2)页岩气含气量测试中损失气量的准确获得,从实测到模型估算都有问题。页岩气等温吸附实验和其数学解释模型可靠程度有待提高,如:实验中使用气体的类型、地层温度和压力下的校正、实验样品的种类等诸多测试对象和环境与页岩气地层原始状态的差异。
3)页岩气在超临界状态下的吸附规律研究较少,相关吸附模型对此鲜有涉及。
4)单一矿物和有机质的吸附特性关注较少,多组分气体中各气体间竞吸机理还未有详细研究。
[1] 徐国盛,徐志星,段亮,等.页岩气研究现状及发展趋势[J].成都理工大学学报:自然科学版,2011,14(6):603-610.
[2] 王瑞,张宁生,刘晓娟,等.页岩气吸附与解吸附机理研究进展[J].科学技术与工程,2013,44(5):279-280.
[3] 李武广,杨胜来,徐晶,等.考虑地层温度和压力的页岩吸附气含量计算新模型[J].天然气地球科学,2012,22(4):76-77.
[4] 解晓翠,常纪恒,于川芳,等.基于吸附理论分析活性炭对卷烟烟气的吸附[J].烟草化学,2012,32(5):124-125.
[5] 刘国杰,黑恩成.气固吸附与Gibbs吸附等温式[J].大学化学,2005,45(4):239-240.
[6] 张健.鄂尔多斯盆地富县区陆相页岩气吸附与解吸附研究[D].成都:西南石油大学,2013.
[7] 张志英,杨盛波.页岩气吸附解吸规律研究[J].实验力学,2012,37(5):447-448.
[8] 郭为,熊伟,高树生,等.页岩气等温吸附/解吸特征[J].中南大学学报:自然科学版,2013,32(2):178-179.
[9] 马正飞,金叶玲,刘艳梅,姚虎卿,等.分形BET吸附模型[J].高校化学工程学报,1994(3):288-291.
[10] 孔德涛,宁正福,杨峰,等.页岩气吸附特征及影响因素[J].石油化工应用,2013,49(7):449-450.
[11] Martini A M, Walter L M, Budai J M, et al. Genetic and temporal relations between formation waters and biogenic methane-Upper Devonian Antrim Shale, Michigan Basin,USA[J]. Geochemicalet Cosmochimica Acta., 1998,62(10): 1699-1720.
[12] Daniel M J, Ronald J H, Tim E R, et al. Unconventional shale-gas systems: The Mississippian Barnett shale of north-central Texas as one model for thermogenic shale-gas assessment[J]. AAPG Bulletin, 2007, 91(4): 475-499.
[13] Hill R J, Zhang ETUAN, Katz B J, et al. Modeling of gas generation from the Barnett shale, Fort Worth Basin,Texas[J].AAPG Bulletin, 2007, 91(4): 501-521.
[14] Ross D J, Bustin R M. Characterizing the shale gas resource potential of Devonian-Mississippian strata in the Western Canada sedimentary basin: Application of an integrated formation evaluation[J]. AAPG Bulletin, 2008,92(1): 87-125.
[15] Grieser B, Shelley B, Soliman M, et al. Predicting production outcome from multi-stage, horizontal Barnett completions[C]//SPE Production and Operations Symposium, Oklahoma: SPE, 2009: 259-268.
[16] Anderson R B, Bayer J, Hofer L J E. Equilibrium sorption studies of methane on Pittsburgh seam and Pocahontas No.3 seam coal[J]. Coal Science,1966, 55(24): 386-399.
[17] Wang K, et al. Application of IAST in the prediction of multicomponent adsorption equilibrium of gases in heterogeneous solids: micropore size distribution versus energy distribution [J]. IEC Res., 2000(39): 527-532.
