记一节有趣的数学实验课

范欣玙 钱晓祺

今天的数学课老师与我们一起进行了从“将军饮马问题”到许瓦兹三角形的实验探究，下课铃声响时，我们还是意犹未尽.我不禁感叹：数学真是奥妙无穷！

老师先用PPT播放唐朝诗人李颀的诗《古从军行》：“白日登山望烽火，黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.我们把这两句诗用数学语言表述如下，并画出相应图形如图1：

将军在观望烽火之后从山脚下的A点出发，走到河旁边的C点饮马，后再到B点宿营.请问：怎样走才能使总的路程最短？

【解决方案】只要从B出发向河岸引垂线，在垂线的延长线上，取B关于河岸的对称点B′，连接B′A，与河岸线相交于C，则C点就是饮马的地方.将军只要从A点出发，沿直线走到C，饮马之后，再由C沿直线走到B，所走的路程就是最短的.即AC+BC=AC+B′C=B′A.此题的本质是利用轴对称的有关知识把线段进行转化，利用“两点之间线段最短”来解决问题.

这使我联想到前天做过的一个思考题：如图2，P为马厩，牧马人某一天从马厩牵出马，先到草地边OA的某处牧马，再到河边OB某处饮马，然后回到马厩.请帮他确定这一天的最短路线.这道题的解题思路其实跟上面问题的本质是一样的（只是本题需用两次轴对称），就是利用轴对称这一数学原理.只要分别作P关于两边的轴对称点P′、P″并连接P′P″，交两边于M、N，此时PM+MN+PN最短.这时得到了一个数学模型：P为定点，在锐角∠AOB内作一个周长最短的△PMN的作法如图3.

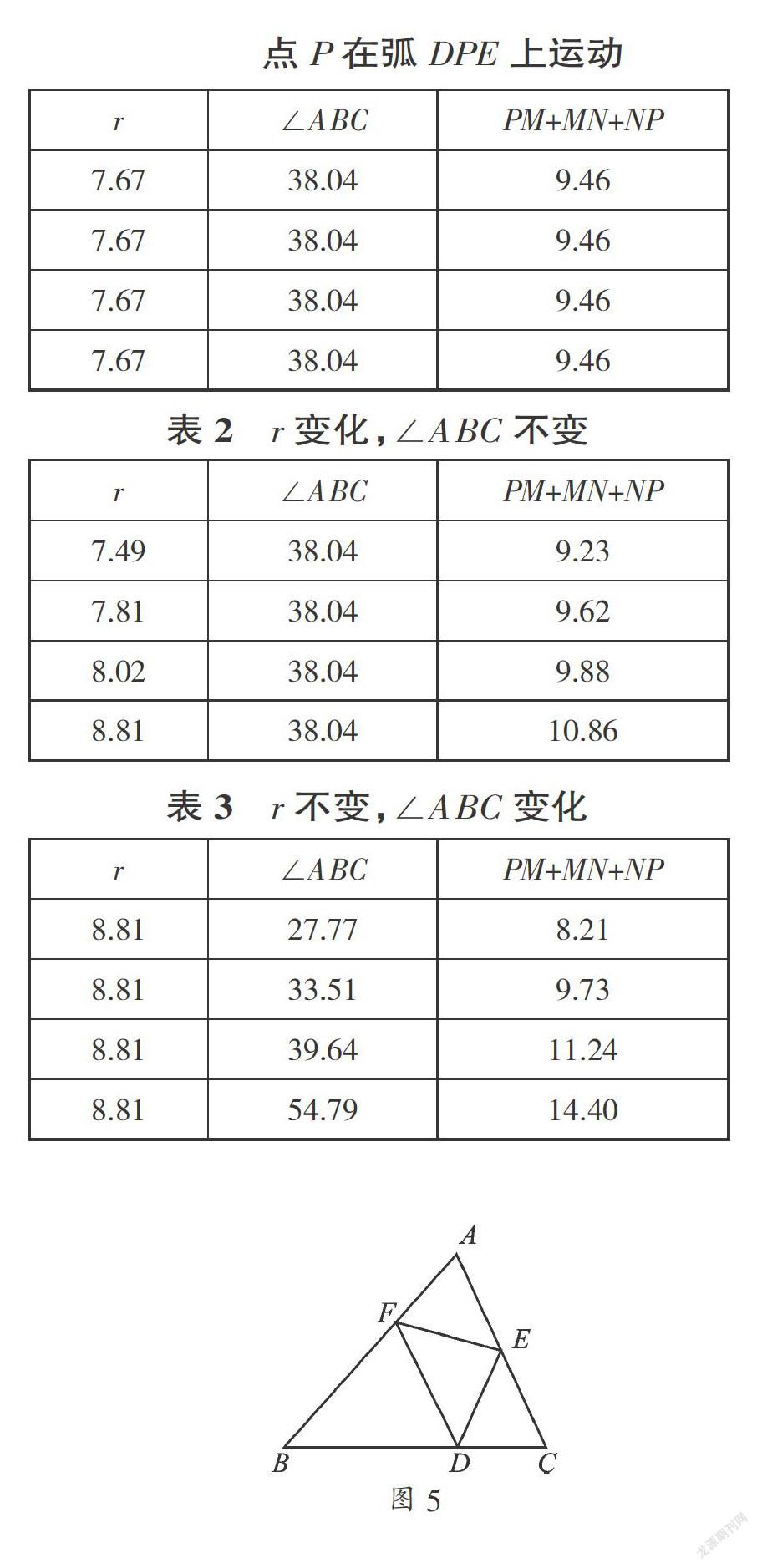
这时老师提出问题2：当点P为锐角∠ABC内一动点时，PM+MN+NP与哪些量有关呢？即其大小由哪些量决定？我的猜想是：可能与点P到角两边的距离、点P到角顶点的距离、∠AOB的大小有关.于是，我们设计了几张表格，设PB=r，以B为圆心，BP长为半径作圆，分别交BA、BC于D、E，如图4.

在老师的帮助下，我们利用几何画板对一些相关数量进行了测量，如表1～3.

表1 r不变，∠ABC不变，

点P在弧DPE上运动

表2 r变化，∠ABC不变

表3 r不变，∠ABC变化

在实验探究中，我们记录并整理数据，再进行合理的推测和猜想，我们得到了如下结论：

（1） 当r为定值，∠ABC为锐角时，随着角度的增加，PM+MN+NP变大.

（2） 当锐角∠ABC为定值时，随着r的增加，PM+MN+NP变大.

老师肯定了上述结论的正确性.接着老师又提出了问题3：在已知锐角三角形ABC中求作一个内接三角形（即顶点分别在△ABC三边上的三角形），使所作的三角形的周长最短.

我尝试画出图形（如图5），我把顶点D、E、F看成动点，发现一时无从下手.老师提示：如果我们把所作三角形的三个顶点都看成是动点不好推理，我们是否可以考虑把其中某个点看成定点来寻找思路.老师的话让我豁然开朗：我先只把图中的E、F看作是动点，那么立刻转化成问题2，把D看作是定点. 分别作点D关于AB、AC的对称点D1、D2，连接D1D2，分别交AB、AC于点F、E，如此一来，E、F就定了.问题的下一步就是要让点D动起来，看点D运动到哪，和通过轴对称变换得到其他两点所围成的△DEF周长最短，于是问题得解.

接下来我再次反思，又有不小收获：由于∠A是定值，那么△DEF的周长就与r（也就是AD）有关，要AD最短，就变成了“点到直线垂线段最短”的模型，那么我们就从点A出发，作AD垂直BC于D.进一步研究发现，若以∠B为考察对象，则当E为AC边上的高与AC的交点，点F、D分别是点E关于BA、BC的对称点的连线与BA、BC的交点，此时△DEF的周长最小.若以∠A、∠C为考察对象，也能得出同样的结果. 即当内接三角形是△ABC的三条高的垂足所成的垂足三角形时，周长最短.

在看到我们的探究成果后，老师啧啧赞叹：你们刚才探究的这个问题就是著名的“许瓦兹三角形”问题，你们真是太棒了！在数学的世界里有许多奥秘等待我们去发现、探索、猜想、证明，而数学实验就是一把打开数学殿堂大门的金钥匙. 在这样的数学实验探究中，我们受益匪浅.

教师点评：这是借助数学软件展开数学实验、结合所学的数学知识解决实际问题的一节实践探究课. 两位学生以课上的动脑思考、动手探究、口头交流等数学活动为主线，细致而独到地阐释了自己的思考和收获.正是在这样的探索与反思中，学生收获了解决问题的方法，使得自己的知识网络建构得愈加完善.对数学的热爱更进了一步.

（指导教师：陶建石）