基于双谱频率估计的快跳频捕获方法

刘 攀， 王 伟， 朱 红

（空间电子信息技术研究院 陕西 西安 710100）

快速跳频（FFH）扩展频谱通信因其良好的抗干扰、抗截获性能，近几十年在军事通信领域和民用通信领域都得到了很大的关注和发展。FFH系统接收可以分为同步和解调两个阶段，其中快跳频同步是决定跳频通信性能的基础和关键[7]。因快跳频通信利用多跳来传输一个数据，使得快跳频自同步法的捕获需要多跳来实现。而在一个数据发送的数跳内传输信息一致但跳频载波频率不一致，又为通过频率估计来实现自同步法的捕获提供了可能性。

研究者们很早就对跳频捕获的方法和性能分析进行了研究[2]。提出了基于能量检测和符号相关检测的并行状态搜索方法来实现捕获，缺点是消耗资源太大[3]。文献[4-6]呈现了目前两种主要的快跳频捕获方案。一种是用同步头与时间信息结合的方法来实现捕获[4-5]，而另一种则基于跳频图案与伪随机序列相结合的双图案的方法来实现捕获[6]。双图案捕获方法的捕获时间与双图案周期成正比，捕获往往需要几十跳甚至上百跳才能完成，除捕获时间较长外，也降低了信道利用率。

针对该现状以及对于跳频同步阶段采用较少频点的系统，文中提出了一种基于双谱频率估计（BFE）的快跳频自同步的捕获方法，并对该方法进行了理论推导和性能仿真，且在此基础上与传统的等待式捕获方法进行了性能比较以及对理论推导的验证。

1 双谱频率估计的捕获模型

捕获可以分为初始捕获和同步识别两个阶段。BFE算法的初始捕获是接收信号的频率估计满足逻辑条件（仅半跳的频率估计有效或当上下半跳频率估计同时有效时，上下半跳估计频点必须在跳频序列中处于相邻或者相同的位置），而传统的初始捕获定义是使接收端与发射端两地的跳频序列的时间误差小于允许值[1]；BFE算法的同步识别是指连续n（n=3）次检测到中频信号，原始的同步识别定义是进一步确认接收机跳频序列与发射机跳频序列的时间误差小于允许值[1]。

接收到的一跳信号在时域上均等地分为上下两个半跳，则上半跳和下半跳之中至少有一个包含单频点[10]。相对于FFT频率估计，利用双谱进行频率估计可以抑制噪声的影响。而单频点正弦信号双谱模值恒为0，需要对信号进行重构[8]。重构后的单频点信号双谱模值为单峰。故通过重构后信号的双谱模值，可以估计上下半跳中仅包含单频点的半跳及其对应频点，从而确定当前接收到信号使用频点在跳频序列中的位置。

BFE算法的初始捕获的流程图如图1所示。

图1 初始捕获流程图Fig.1 Flow chart of initial capture

在初始捕获阶段，把本地跳频码发生器的输出固定在某个值，使频率合成器输出保持为最低的跳频频点。把接收到的信号进行解跳后进行2N点采样，得到的信号为式（1）所示。

其中ak为第k跳解跳信号幅值，ωk为解跳后的角频率，φk为[0，2π]上均匀分布的随机相位。采样信号在时间上均等地分为上半跳和下半跳，得到：

上半跳为例，对信号进行重构，得到：

图2 同步识别流程图Fig.2 Flow chart of synchronization identification

利用双谱模值分别估计上半跳和下半跳的频点，在跳频序列所有频点的双谱模值中，当最大值与次最大值的比值大于门限ho时，表示估计信号的频点的单一。此时有两种情况：1）上下半跳估计的双谱模值同时表现为单峰，当两个估计频点在跳频序列上“相邻”或者“相同”时，估计有效；2）上半跳或下半跳信号的双谱模值其中一个为单峰，表明仅该半跳的估计有效。当情况1）或者情况2）出现时，初始捕获完成，进入同步识别阶段；否则继续保持初始捕获阶段，当捕获次数到达门限终止捕获，表明捕获失败。

初始捕获完成后，进入同步识别阶段。同步识别的流程图如图2所示。

在同步识别阶段根据初始捕获阶段估计的频点来改变本地跳频码发生器，使本地频率合成器输出调整为所估计频点下一跳对应的频点。本地频率合成器输出根据初始捕获阶段的情况也分为两种情况：1）针对初始捕获全跳估计有效，但是上下半跳估计的频点不一致，移动到下半跳所估计频点，再超前移动半跳；2）针对全跳估计有效且上下半跳估计频点一致或半跳估计有效的情况，直接移动到估计频点所对应的下一跳频点。

此后对信号解跳和滤波，滤波器的中心频点为中频频点，带宽为两倍的码元速率。滤波后对信号采样和重构，利用其双谱模值检测中频信号。如果不存在中频信号，那么返回初始捕获阶段；如果存在，则更改跳频序列发生器，使频率合成器输出频率为当前频点对应的下一跳频点。重复上述流程，当且仅当连续n（n=3）次都检测到中频信号的存在时，则认为捕获成功。同步识别阶段信号模型与式（1）～式（5）相同。

2 性能分析

设进行单次捕获的捕获概率和虚警概率分别为PD和PF。当进行m（m>n+2）次捕获时，此时各个概率为：

关于捕获时间，设一跳的周期为Th，故m次捕获时间的均值为：

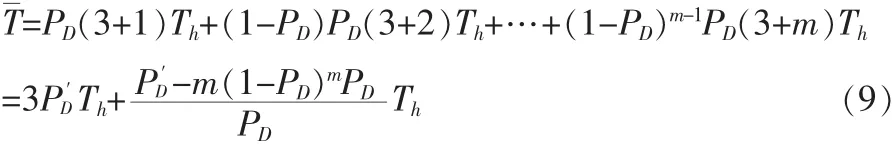
3 仿真结果与分析

文中对提出的基于双谱频率估计捕获模型进行了仿真，并验证了理论推导的性能分析模型。考虑到传统的捕获方法中匹配滤波法消耗资源大的问题，在性能分析上仅与传统采用滑滑动相关的等待式捕获进行性能比较。跳频频点选按时间顺序选为 312 MHz，327 MHz，317 MHz，322 MHz，337 MHz 6个频点，此时M=6。接收端本地载波频点对应为307 MHz，322 MHz，312 MHz，317 MHz，332MHz。

快跳频系统的分集数为20，调制方式采用二进制频移键控（BFSK）。 同步用的训练序列全部发“1”，发“1”对应的调制载波频率为1 MHz。中频信号频点为6 MHz，码元速率为1M Baud。对解跳后的信号以64MHz采样频率进行采样。BFE算法初始捕获阶段的带通滤波器带宽为30 MHz，起始频率为6 MHz；在同步识别阶段滤波器带宽为2 MHz，中心频点为6 MHz。分别把捕获次数设为6，12和18。在高斯白噪声信道中，信噪比为0 dB到12.5 dB之间进行仿真。作为对比的传统等待式捕获，采用同样的频点和带通滤波器。

把同步识别阶段n取为3，图3和图4分别为m=6和m=1时，BFE算法与传统等待式捕获在信噪比为0 dB虚警概率接近的条件下，捕获性能和虚警概率的比较。

图3 m=6捕获性能与虚警概率比较Fig.3 Performance compare in capture possibility and alarming possibility with m=6

图5 m=6，12，18 BFE算法捕获性能与虚警概率Fig.5 Performance compare in capture possibility and alarming possibility of BFE algorithm with different capture times thresholds

仿真结果表明，相对于传统等待式捕获，BFE算法在捕获性能上，与传统算法有相同捕获概率时，低信噪比下可使所需信噪比下降4 dB。高信噪比下可使所需信噪比下降6 dB。性能提升。传统等待式捕获其虚警概率随信噪比增大下降速度远快与BFE算法。由式（8）可以知道BFE算法其虚警概率存在指数项，当m较大时，随着捕获概率而减小缓慢，致虚警概率下降缓慢，但仍然在可接受的范围。

图5为m=6，12和18时，BFE算法的捕获性能和虚警概率的比较，在各对应信噪比下，以m=6时捕获概率为基础，对应m=12和m=18的捕获概率满足式（6）理论推导，且误差小于3E-3，表明仿真结果与理论相符。而虚警概率随着m的增大而增大，且随着m增大而增大速度变缓也与式（8）推导相符。

此外，在m=6时，信噪比为4 dB时即可实现100%捕获，虚警概率为，而m=12时，信噪比3 dB即可实现100%捕获，对应的虚警概率为3.16E-4。m=18，信噪比为2 dB时即可实现100%捕获，虚警概率为。可以根据信道的状况和虚警概率要求来折中选择捕获的次数。

4 结 论

文中提出了一种快跳频自同步法同步的基于双谱频率估计（BFE）的捕获方法，对其捕获概率和虚警概率进行了理论推导和性能仿真，并在此基础上对理论推导进行了验证，以及和传统的等待式捕获方法进行了性能比较。仿真的结果表明BFE算法具有良好捕获性能，在很少的几跳内即可实现捕获，且保持较低的虚警概率。在信噪比为0 dB与传统等待式捕获有相同虚警概率的条件下，捕获次数门限为跳频序列长度时，低信噪比下，BFE算法相对于传统的等待式捕获在相同捕获性能时可使所需信噪比下降4 dB，高信噪比时达到相同捕获概率时可使所需信噪比下降6 dB。当信噪比为4 dB时，BFE算法在9跳内即可实现100%捕获，且保证虚警概率为3.16E-5。捕获次数门限可根据信道状况以及虚警概率需求做出折中选择。

[1]梅文华，王淑波，邱永红，等.跳频通信[M].北京：国防工业出版社，2005.

[2]HONG Zhao，QIANGWang.On frequency hop synchronization in multipath rayleigh fading[J].IEEE trans.Vehicular Tech.， 1998， 47（3）:1049-1065.

[3]ZHAO Hua-rong，ZHAO Ming-sheng，LUO Kang-sheng.Fast acquisition schemewith excellentanti-jammingperformance[J].Journal of Tsinghua University:Science and Technology，2007，47（4）:546-550.

[4]刘春玲，刘照舵，刘海燕.一种低轨卫星跳频通信同步捕获方法[J].计算机仿真，2014，31（3）:87-91.LIU Chun-ling，LIU Zhao-duo，LIU Hai-yan.Synchronization capturemethod for frequency hopping communication system on LEO[J].Computer Simulation，2014，31（3）:87-91.

[5]LI Fei-long，LI Zhi-qiang，LOU De-kan，et al.Analysis and research of synchronization technique for frequency hopping communication systems[C]//IEEE Computer and Network Technology Conference， China，2011:1968-1972.

[6]程郁凡，李少谦.FFH/BFSK系统的一种基于频率和PN序列双图案的早迟门同步捕获方法[J].电子与信息学报，2009，31（3）:666-670.CHENG Yu-fan，LI Shao-qian.Synchronization acquisition using early-late gate based on frequency-PN sequence double pattern for FFH/BFSK spread-spectrum systems[J].Journal of Electronics&Information Technology，2009，31（3）:666-670.

[7]Nikias C L，Raghuveer M R.Bispectrum estimation:Adigital signal processing framework[J].Proc.IEEE.，1987，75（7）:869-891.

[8]Lohmann AW，Wirnitzer B.Triple correlations[J].Proc.IEEE，1984（72）:899-901.