地下矩形管道横截面抗震计算中拟静力方法的应用

□ 王雪彦 姜天华 曹文龙

一、地下结构抗震计算基本原理

在地震作用下，地下结构的地震响应很大程度上依赖于地层的地震响应，地层的位移分布和周面剪切力是起决定作用的因素，而惯性力的影响一般比较小。因此，地下结构的抗震计算方法与地上结构也有很大不同。目前地下结构的抗震计算方法主要有拟静力计算方法和动力反应分析方法两类，动力反应分析方法能够正确反映结构的地震响应，但计算量大，计算时间长，对计算结果的评价比较困难，所以，对于一般的地下结构，仍主要采用拟静力法进行计算，包括反应位移法和地震系数法。

(一)反应位移法。反应位移法是《核电厂抗震设计规范》(GB50267-1997)推荐的地下结构地震反应计算方法。其基本思想是认为地下结构的地震响应取决于周围地层的运动，将地层在地震时产生的位移差(相对位移)通过地基弹簧以静荷载的形式作用在结构物上，从而求得结构的内力。将反应位移法用于地下结构横断面的抗震计算中时，主要需考虑3种地震作用:地层变形、地层剪力以及结构自身的惯性力，如图1所示。

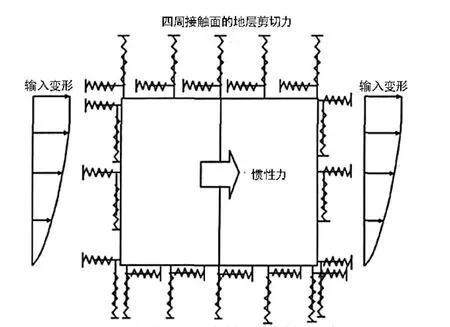
图1 反应位移法抗震计算示意图

(二)地震系数法。地震系数法是《铁路隧道设计规范》与《铁路工程抗震设计规范》规定采用的地震反应计算方法。地震系数法是由地面结构抗震理论发展而来的，根据地震峰值加速度确定水平地震系数进行计算，一般只计算水平地震力的作用，包括结构自重的水平地震力、侧向土压力增量、地震作用下围岩弹性抗力以及地震时坍塌及落实冲击力，本文只计算结构自重的水平地震力F11、F12、F13以及廊道一侧土体的土压力增量Δe、P，如图2所示。

图2 地震系数法抗震计算示意图

水平地震力，作用于土柱质心:

当需要地层提供的水平抵抗力大于地层能够提供的被动土压力时，可认为地层水平抵抗力的值即为地层的被动土压力:

当需要地层提供的水平抵抗力小于地层能够提供的被动土压力时，地层水平抵抗力的值可按静力平衡条件计算。

式中:ɳc——综合影响系数，与工程重要性、廊道埋深、地层特性等有关，规范中建议对于岩石地基，对于非岩石地基;Kh——水平地震系数，7度地区，8度地区，9度地区，本文取0．21;m——廊道上部土柱的质量;γ——围岩重度，kN/m3;hi——距地面高度，m;θ——地震角，°本文取 3°;λ——地震力作用下侧压力系数;λ＇——无地震力作用下侧压力系数;φ——围岩计算摩擦角(°)。

二、算例

(一)基本参数。本文以某一实际工程中的地下廊道作为算例，计算地下结构的地震响应。廊道高3．5m，宽5．7m，壁厚0．4m，埋深1．7m，采用C35混凝土。地表以下土体材料参数和计算厚度见表1。基岩面速度反应谱为0．246m/s，土层自振周期为0．231s。

表1 土层物理参数

(二)计算模型。

1．地基弹簧系数。取一定深度和宽度的土体，使地下结构沿底板或侧墙的法向移动δ，然后计算出地下结构上各节点在该方向的反力Ri，得出每根弹簧的刚度ki=Ri/δ，再将弹簧的刚度换算为相应的地基弹簧系数。对于结构切向的弹簧系数，可按照相同的方法，对结构施加沿底板或侧墙切向的位移来计算。

图3

2．计算模型。廊道侧壁、顶板、底板采用二维梁单元beam3模拟，廊道与土体的接触采用combin14单元模拟，combin14单元的属性为上文计算出的弹簧刚度。

3．地震作用。

(1)反应位移法。假设地层为单一均匀地层，地层的运动微分方程为:

式中，u为地层变位，γs为地层重度，Gd为地层动剪切弹性模量，Cs为地层黏性衰减系数，uB为地层地震动，g为重力加速度。通过求解(5)式并作近似处理可得地层最大位移为:

式中，Su为地层基岩面的速度反应谱，Ts为地层的自振周期，z为原点位于地表的向下坐标系变量，H为土层厚。

(2)式对z求导并与地层剪切模量相乘得对应天然地层的剪切力:

本工程中，根据基本参数，求得uh(z)=0．00920cos(0．218z)，ʅh(z)=0．0863sin(0．218z)。

(2)地震系数法。人工填土内摩擦角为30°，地震角按照地震烈度为8度由表1取3°。计算得:

Δe1=γh2(λ - λ＇)=20 × 4．95 × (0．376-0．333)=4．257kN/m2

假设，需要地层提供的水平抵抗力大于地层能够提供的被动土压力，则水平抵抗力P的值为:

此值远大于动土压力与结构自身惯性力之和，所以P值可根据静力平衡条件求得。

4．计算结果

图4 弯矩

三、结语

本文分别介绍了反应位移法和地震系数法这两种常用的拟静力计算方法，结合具体算例，分别采用两种方法进行计算。通过两种方法的计算结果看出，廊道的最大弯矩出现在侧壁底部，最大弯矩出现在转角部位，这与本廊道的结构形式为框架结构有关，受力形式是合理的。反应位移法和地震系数法作为地下结构抗震计算的简化方法，二者都可实现对地下结构地震反应的近似计算，本文以矩形管道进行计算，其方法也可应用于其他类型结构。