普立特悬索桥抖振响应时域分析

黄文锋, 邹孔庆,2, 孙建鹏, 王美芹

(1合肥工业大学，安徽 合肥 230009；2中铁四局集团钢结构有限公司，安徽 合肥 230022；3西安建筑科技大学，陕西 西安 710055)

普立特悬索桥位于云南省宣威市境内，横跨深度近400m的普立大沟，是普宣公路全线关键控制性工程之一．设计采用主桥960 m的双塔单跨悬索桥，主桥跨径布置为166+628+166 m．主缆横向布置两根，主缆横桥向中心间距为26 m．上部结构主桥采用628 m单跨简支钢箱加劲梁悬索桥，普立岸主墩塔高154.3 m，宣威岸主塔高162.2 m，主缆边跨均为166 m，索塔采用直塔柱门式框架结构，基础采用群桩基础，普立岸采用隧道锚，宣威岸采用重力锚．下部结构采用等截面钢筋混凝土矩形墩、群桩基础，普立岸采用重力式桥台，宣威岸采用肋板式桥台，桥型布置如图1所示．

图1 普立特悬索桥桥型布置图Fig.1 PLT suspension bridge

大跨度桥梁属于轻柔结构．其风致振动会给过往车辆及行人安全带来很大影响，容易引起桥梁结构局部构件的疲劳问题[1]，有必要对其风致抖振问题进行研究．桥梁在随机风荷载作用下的响应计算主要包括频域法和时域法两类．频域分析方法较为简单，但其需要计入一定数量的模态，得到的响应值为数字特征，并且只能进行线性分析．而时域法一般将结构进行有限元法离散后进行时程分析，可以得到其各种响应的时程，计算结果较为清晰简单，同时可以深入理解各种非线性因素对大跨度桥梁空气动力特性的影响．国内外一些学者对大跨度桥梁结构非线性抖振时域分析都进行了较为深入的研究[2]．但时域分析的不足之处在于公式分析求解难度较大，采用数值分析需要较高的计算机内存，耗时．但随着计算机技术的发展，这些问题基本上都可以解决，抖振响应时域分析法已经成为桥梁抗风设计研究的重要课题[3]．

进行时域分析的核心是得到荷载时程，因而抖振力的随机模拟成为首先要解决的问题，目前采用的方法通常是根据已知的脉动风功率谱模拟得到对应的风速时程，再由准定常理论将风速转化抖振力时程，编写相应的循环加载抖振力数据的程序，并在ANSYS的MATRIX27单元加入气动刚度矩阵和气动阻尼矩阵考虑自激力作用[4]，最后利用ANSYS软件循环读入相应数据到桥梁结构节点上，求解动力方程，获取桥梁时域内的抖振响应分析结果．本文对云南普立特大桥的抖振响应的时域分析采用了与上述相同的分析方法．

1 脉动风模拟

本研究借鉴 George Deodatis 的谐波合成法模拟了云南普立特大桥处的空间脉动风场[5,6]．在该桥梁有限元模型上共设置n个风荷载施加点，对应的形成 n维零均值平稳高斯随机过程向量 f(t)，如下所示：

其中，N为充分大的正整数；Δω为频率增量，等于ωup/N，ωup为截止圆频率，当 ω＞ωup时，S0(ω)=0；Фml为均匀分布于[0,2π]区间的随机相位角；Hjm(ωml)为矩阵 H(ω)正的元素，H(ω)是 S0(ω)的 Cholesky 分解，其中 S0(ω)、H(ω)如下式（3）及（4）所示；θjm(ωml)为 Hjm(ωml)的复角．

综上所述，已知 S0(ω)，适当选择 N、ωup、Δt就可以获得好的随机过程样本；同时采用FFT（傅里叶变换技术）技术，大大提高了该类方法的计算效率.

针对大跨度桥梁而言，整个主梁基本处于同一高度，可近似认为沿主梁布置的n个模拟点具有相同的平均风速和水平脉动功率谱．

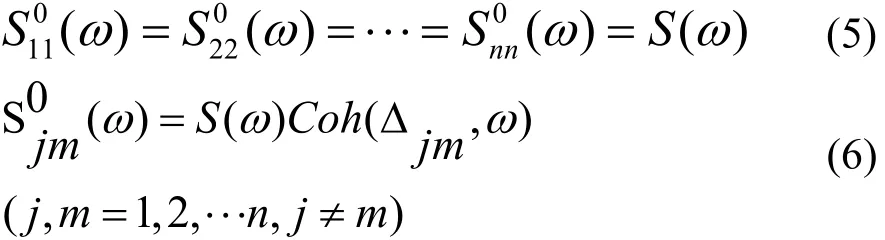
其中：Δjm为 j、m 两点间距离；Coh(Δjm,ω)为相干函数．

考虑到桥面上模拟点为等间距布置(除主梁离桥墩较近的点，但距离相差不大)，间距为Δ，则有Coh(Δjm,ω)采用 Davenport相干函数.

对主塔而言自然风的风速正交谱很弱，一般可忽略，故沿主塔高度上各点的互功率谱表达式为(j≠m)：

2 抖振力计算

模拟得到脉动风速时程后，就可将其转化为作用于结构上的风荷载时程．通常将风致风荷载分为三部分：平均风引起的静风力、脉动风引起的抖振力和气动耦合产生的自激力，其中静风力计算公式可参见文献 [7]，自激力计算公式见下文，抖振力的计算公式参见文献[8]，具体来说脉动风作用下桥梁单位展长的抖振力计算公式如下所示：

其中：Lb(t)、Db(t)、Mb(t)分别为在初始风轴坐标系下的气动升力、阻力及扭矩；ρ为空气密度；U为设计基准风速；B为桥梁主梁的计算宽度；u(t)、w(t)分别为顺风向及垂直向脉动风速；CD、CL、CM和DC′、LC′、MC′分别为主梁初始风攻角方向上的气动阻力、升力和扭矩系数及其导数．为便于在有限元中实现，常将抖振力转换为节点坐标系下的节点集中力，采用集中法，将单元上的三分力堆积到节点上，以集中力的形式施加到有限元模型上，其风轴坐标系的抖振力的转换节点坐标系关系如下所示：

其中：Fy、Fz、FM分别为节点坐标系下的抖振力项，α0为初始风攻角.

对于主塔和桥墩，仅考虑其抖振阻力的作用，单位长度上的主塔抖振阻力的表达式为

其中，Bz为桥塔和桥墩在迎风面的投影面积；CD为主塔的阻力系数．

为便于计算，通常将实际非线性的抖振力进行准定常假设下的线性化处理，忽略其中小量的耦合作用，虽然对结构计算精度有所影响，但对一般桥梁而言计算精度是满足要求的．

3 自激力计算

自激力是风场和弹性体之间的相互作用．为方便在 ANSYS中实现，此处采用曾宪武等人在Miyat[9]准定常气动模型基础上，通过进行双泰勒级数展开导出的 12阶气动刚度矩阵和气动阻尼矩阵来表达自激力[10]．

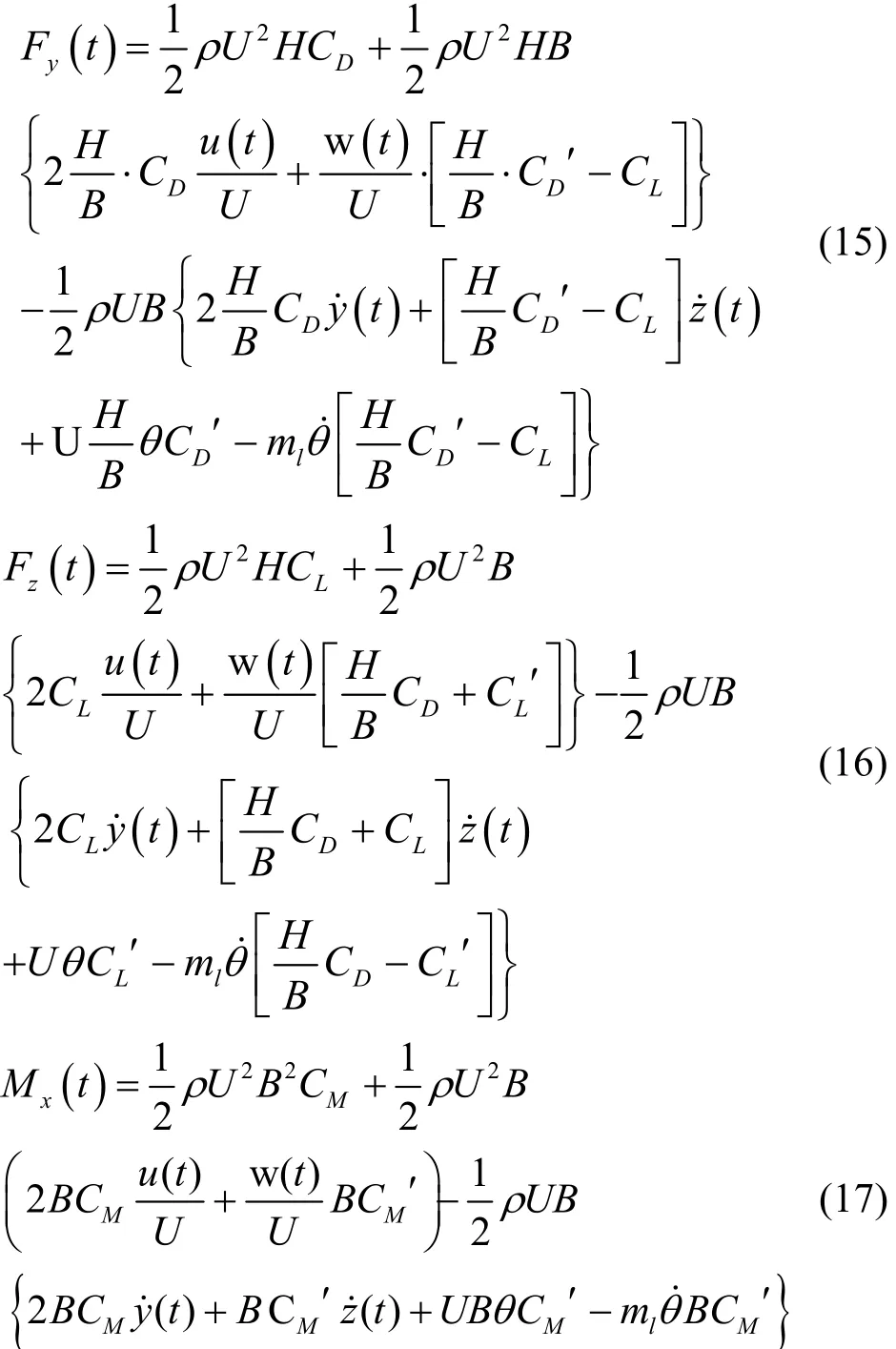
其中：()yt˙、()zt˙、θ˙分别为主梁截面处的速度和角速度；ml为主梁的特性长度．

从而，单位展长主梁截面上的自激力表示为

式中：K0、C0为单位展长气动刚度、阻尼矩阵，其具体表达式见曾宪武等人的研究[11]；δ(t)、(t)δ˙为单元位移向量以及速度向量．

利用 ANSYS的自定义单元 Matrix27[4]，可以直接定义质量、刚度、阻尼矩阵，各矩阵的参数作为实常数来输入，气动自激力属于非保守力，采用的是非对称矩阵．气动刚度矩阵和阻尼矩阵要分别建立单元，不能共用一个Matrix27单元．主梁跨中区域施加各参数值为端部四个单元（分别为两个气动刚度矩阵和气动阻尼矩阵）的两倍．

4 抖振响应分析

4.1 建模及风荷载

对结构进行有限元离散，有主缆、吊索、主塔、加劲主梁、桥墩等组成．主缆和吊索采用Link8单元模拟，主塔和桥墩采用Beam4单元模拟，加劲主梁采用Beam4单元模拟，主梁与主塔连接采用弹簧-阻尼单元Combin14和Mass21．利用ANSYS软件建立了其三维有限元模型，全桥模型共有908个节点，869个单元，其中主缆单元164个，吊索单元102个，主塔和桥墩单元336个，主梁单元152个，其它的均为质量元．主梁采用空间鱼刺模型，刚性鱼骨刺横梁和主塔通过主缆连接横梁.此全桥空间有限元模型如图2所示．在悬索桥结构的仿真模拟中, 主梁节点和吊索吊点采用刚性连接模拟，桥塔与主缆间采用刚性连接，主梁与桥塔采用弹性连接顺桥向采用有阻尼约束方式模拟，全桥结构的边界条件为两个桥塔的底部完全固结，主缆在两侧锚定固结，在塔顶固结对于大跨度悬索桥而言，以恒载下的非线性静力分析为基础，动力响应是以恒载变形后的状态下分析的，目的是验证结构处于平衡状态时的几何位置是否合理．

图2 全桥有限元模型Fig.2 Finite element model of PLT suspension bridge

对大跨度悬索桥进行动力特性分析得到其前十阶振型如表1所示．由表可知，普立特悬索桥的基本周期为8 s左右，表现为主梁侧向漂移和反对称竖弯，频率主要分布在0.12～1 Hz内，其分布较为密集，同时桥塔振动为主的振型出现较晚如桥塔反对称侧弯在31阶发生，频率约为0.84 Hz，故桥梁的动力特性主要表现为前几阶振型．

表1 桥梁的自振频率及振型Table 1 Frequencies and modes of bridge

利用前述介绍的脉动风速的谐波合成法，采用Matlab编制相应脉动风模拟程序，对本桥主要的模拟参数如表 2所示．相干函数 Cohij(ω)如图 3所示．从图中可以看出，相关函数对其频率的敏感度较强，当空间间距一定时，频率越小，其相关函数越大.

表2 脉动风场模拟主要参数Table 2 Main parameters for fluctuating wind simulation

图3 空间相干函数Cohij(ω)Fig.3 Spatial coherence function Cohij(ω)

模拟得到的主梁顺风向及垂直向脉动风速时程结果如图4所示．模拟得到的垂直向脉动风速功率谱与目标谱的对比如图 5所示．通过对比可知，数值模拟得到的风场与目标吻合较好，验证了模拟方法和所编写模拟程序的可靠性及有效性．

图4 主梁跨中点模拟得到的顺风向、垂直向脉动风速时程Fig.4 Time history of simulated longitudinal and vertical fluctuating wind speeds at middle point of the main span

图5主梁跨中点垂直向脉动风速功率谱对比Fig.5 Comparison of fluctuating wind spectrum at the middle point of main span

4.2 计算结果分析

脉动风速时程模拟完成后，采用基于准定常理论的抖振力计算公式，就可以将风速时程转化为作用于桥梁的等效抖振力时程，此过程通过在Matlab软件中生成数据文本并考虑节点的等效迎风面积，并利用ANSYS中的APDL进行二次开发即可实现，其中主梁在风轴坐标系下的气动三分力系数如图 6所示．结构的自激力分析采用 ANSYS自带的MATRIX27单元输入其气动刚度矩阵和气动阻尼矩阵的参数完成．计算中分别考虑了-12°～12°共25种工况，此处仅以0°工况为例进行结果分析．将得到的抖振力时程施加于该桥的有限元模型，编写相应的循环加载批量数据和后处理程序，计算时间取1000s，分别计算了考虑与不考虑自激力作用时该桥的抖振响应，结果如图7所示．计算中考虑结构的几何非线性的因素，对此桥而言，几何非线性主要来源于缆索的垂度效应、结构初应力和结构大变形三个因素的影响，采取措施是在ANSYS中打开几何大变形开关（Nlgeon，on）、应力刚化（Stess stiffening）、更变坐标（upcood，1，on），并采用的Newmark-β方法计算桥梁的抖振响应．

图6 普立特悬索桥气动三分力系数Fig.6 Aerodynamic coefficients of Pu Li Te bridge

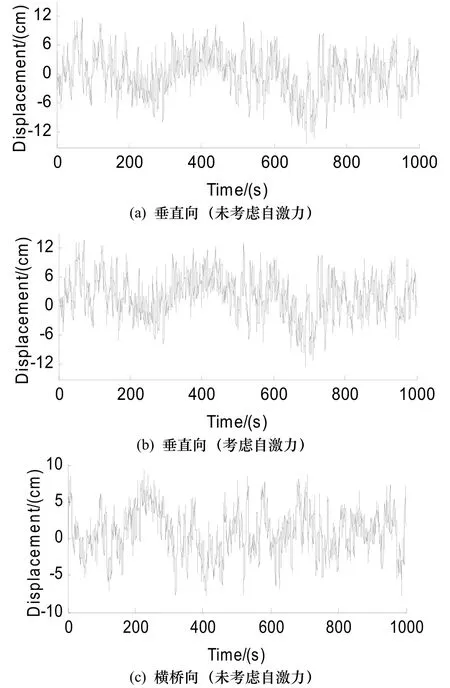
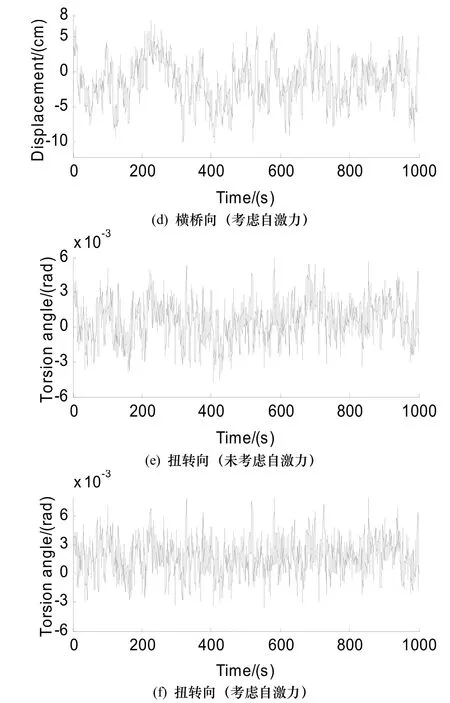
图7 考虑和不考虑自激力作用下主梁跨中点的抖振响应Fig.7 Buffeting responses at the middle point of main span with and without considering self-excited forces

由图可知，不考虑自激力作用时，主梁跨中节点处的垂直向、横桥向及扭转向抖振位移均以零为均值上下波动．通过对计算结果进行统计可知横桥向位移响应的均方差为6.12 cm比垂直向位移响应的均方差5.08 cm大20%左右．考虑自激力作用时，垂直向位移响应均值有下降的趋势，振动幅度也略有下降，此时自激力起到微弱的正阻尼作用．横桥向及扭转向位移响应均值均略有上升的趋势，但整体振动幅度变化不是很明显．总之，对本桥考虑了自激力作用后，较为明显的作用是改变了桥梁振动的平衡位置，但自激力所起的正阻尼作用效果不明显．

6 结论

本文根据普立特大跨度悬索桥的结构形式特点，结合脉动风相关特性，利用Deodatis的谐波合成法，很方便的对普立特大跨度悬索桥的脉动风场进行了模拟，并对模拟效果进行了检验，验证了所采用模拟方法和所编模拟程序的可靠性及有效性．

通过利用ANSYS软件完成了脉动风作用下普立特大跨度悬索桥桥梁考虑与不考虑自激力作用时的抖振响应计算．通过研究发现，考虑与不考虑自激力时计算得到的该桥抖振响应的振动幅度变化不大，主要作用在于改变了桥梁振动响应的平衡位置，自激力在局部方向(垂直向)的响应起到正阻尼的作用，另外，横桥向桥梁抖振位移响应的均方差比垂直向大20%左右．整体来看，从桥梁抖振位移响应时程可以获取比较全面的结构抖振力变形信息，为类似桥梁的抗风设计提供参考．

References

[1] 李小珍, 蔡 倩, 强士中. 芜湖长江大桥主跨斜拉桥列车走行安全性与舒适性[J].交通运输工程学报, 2002,2(3): 34-40.LI Xiaozhen, CAI Jing, QIANG Shizhong. Train running safety and comfort analysis of the cable-stayed bridge on Wuhu Yangtze-river Bridge [J]. Journal of Traffic and Transportation Engineering, 2002, 2(3): 34-40.

[2] DING Quanshun. Computer simulation of buffeting actions of suspension bridges under turbulent wind [J].Computers and Structures, 2000, 76(6): 787-797.

[3] 项海帆,陈艾荣. 特大跨度桥梁抗风研究的新进展[J].土木工程学报, 2003, 36(4): 1-8.XIANG Haifan, CHEN Airong. Recent advances in research on aerodynamics of extra long span bridges[J].China Civil Engineering Journal, 2003, 36(4): 1-8.

[4] ANSYS Inc. Theory reference and ANSYS APDL programmer’s guide [M]. http://www.ansys.com.cn

[5] ROSSI R, LAZZARI M, VITALIANI R. Wind field simulation for structural engineering purposes [J]. Numerical Methods in Engineering, 2004, 61(5): 738-763.

[6] DEODATIS G. Simulation of ergodic multivariate stochastic processes[J]. Engineering Mechanics, 1996,122(8): 778-787.

[7] HOLMES J D. Wind Loading of Structures[M]. 2nd ed.Taylor & Francis, Abingdon, 2007.

[8] SARKAR P P, JONES N P, SCANLAN R H. Identification of aeroelastic parameters of flexible bridge [J]. Engineering Mechanics, 1994, 120 (8):1718-1741.

[9] MIYATA T, YAMADA H, BOONYAPINYO V, et al.Analytical investigation on the response of a very long suspension bridge under gusty wind, Proc., 9th Int. Conf.on Wind Engineering, New Delhi, India, 1995, 1006-1017.

[10] 曾宪武, 韩大建. 大跨度桥梁风致抖振时域分析及在ANSYS中的实现[J]. 桥梁建设, 2004(1): 9-12.ZENG Xianwu, HAN Dajian. Time-domain analysis of wind-induced buffet on long-span bridges and implementation of analysis in ANSYS [J]. Bridge Construction, 2004(1): 9-12.