机载预警雷达海面多目标航迹起始算法研究
2015-01-22
(空军预警学院,湖北武汉430019)
0 引言
航迹起始是机载预警雷达海面多目标跟踪首先要解决的问题[1-2]。由于舰船目标外形通常较为复杂,雷达量测噪声表现出明显的非高斯噪声特性[3]。同时,舰船目标具有相互靠近的特点,加之目标数量众多(包括渔船、大型货船和军舰等),使得机载预警雷达探测海面多目标时存在航迹中断、跳点较多和无法形成稳定航迹等问题。因此,海面多目标航迹起始问题是机载预警雷达海面多目标跟踪问题的难点。
传统的雷达航迹起始算法研究目前已较为成熟,可分为4类:①将航迹起始看作检测问题,典型的算法包括序列概率比检验(Sequential Probability Ratio Test,SPRT)[4]、贝叶斯法(Bayes Track Confirmation,BTC)[5]等。其中,BTC将滤波残差引入到统计决策中去[5],性能优于SPRT,但后验概率的计算依赖于统计模型,不利于工程实现。②序贯处理算法,典型的算法包括启发式直观法(Heuristic Rule Method,HRM)[6]、逻辑法(Logic Based Method,LBM)[1]等。其中,HRM利用运动学原理,对连续扫描的量测数据加以运动特性约束。LBM采用相关波门对量测数据进行统计判决,在稀疏杂波环境下能有效起始航迹。③批处理算法,典型的算法包括Hough变换法(Hough Transform,HT)[7]及其改进算法等。Hough变换法被广泛应用于模式识别和图像处理[7-8]。修正的Hough法采用递归的方法,通过对量测数据的过零交汇点的约束,能获得比Hough变换法更优的性能[9]。④仿生智能算法[10],包括遗传算法、蚁群算法等。海面多目标航迹起始问题实质上是噪声起伏条件下,密集多目标航迹起始问题。传统的航迹起始算法会产生航迹分裂和航迹合成,致使目标重复起批。此外,参数起伏会使得航迹起始算法鲁棒性降低。
针对以上问题,本文在现有航迹起始算法的基础上,从航迹起始的初始波门设计、相关波门设计、关联准则环节入手,提出了一种适用于机载预警雷达海面多目标的航迹起始算法。该算法能有效解决目标密集条件下多目标航迹起始问题,同时算法对量测噪声具有较好的鲁棒性。
1 机载预警雷达海面多目标航迹起始算法
海面多目标航迹起始就是判断机载预警雷达获得的量测数据是否源于真实目标,并建立临时航迹和目标状态的初始估计。舰船目标的运动方程由下式描述:
式中:X(k+1)=[x,v x,y,v y]′为第k+1时刻的目标状态向量;v(k)为零均值高斯白噪声矢量;F,Γ分别为状态转移矩阵和噪声分布矩阵。机载预警雷达在载机坐标系中对舰船目标的方位θ及斜距ρ进行量测,是对状态矢量的非线性量测,即
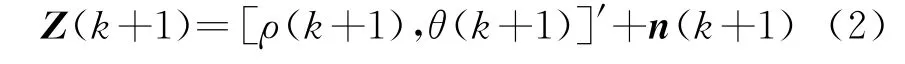
式中,n(k+1)为量测噪声矢量。假设Z i(k),Z c j(k)分别表示第k时刻第i个目标量测数据和第j个海杂波虚警量测数据,其中i=1,…,n(k),j=1,…,m(k)。那么直到第k时刻,雷达接收的所有量测数据集合可表示为

海面多目标航迹起始就是要从包含海杂波影响的量测数据集中提取出真实目标的量测序列。
针对现有航迹起始算法难以有效解决机载预警雷达海面多目标航迹起始的问题,本文提出了一种新的机载预警雷达海面多目标航迹起始算法,具体步骤如下:
1)运用改进的初始波门,利用三帧的量测数据建立航迹头,并进行航迹外推(通过多项式外推或卡尔曼滤波实现)。
2)对第k(k>3)时刻的量测数据,运用改进的相关波门,与第k-1时刻的外推航迹进行波门判据,并更新逻辑位和航迹状态:波门内有候选量测且多条临时航迹共用一个量测则运用最大似然关联准则;波门内有候选量测且无共用现象则逻辑位赋值为1,并更新航迹状态;波门内无候选量测,则逻辑位赋值为0,并用外推值更新航迹。
3)将处理后的临时航迹通过M/N的滑窗逻辑判断,满足逻辑准则的升级为确认航迹,否则删除或保留以待下一步判断。
4)对未被关联的剩余量测,再与第k-1时刻的自由量测关联判断,形成新的临时航迹头。
5)重复上述步骤,直到形成稳定航迹。
下面对所提海面多目标航迹起始算法中的关键环节进行详细介绍。
1.1 延迟初始波门设计
初始波门设计的目的在于保留真实目标的航迹,避免出现航迹分裂与航迹合成现象。因此本文利用三帧量测数据构建一种延迟判决逻辑。其设计思路如下:
1)首先通过构造统计检验量D ij(k)形成检验波门。通过χ2分布检验,对前两帧量测数据进行判决。判决表达式如下:
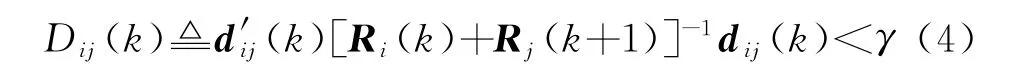
式中:d ij(k)为量测矢量距离[6];R i(k),R j(k+1)为k时刻与k+1时刻的量测噪声去偏转换的协方差矩阵;γ为判决门限。
2)如果波门内候选量测来自唯一的量测源,则与此量测构成初始航迹头。如果出现航迹分裂现象,则再次构建波门,利用第3帧数据判断:①如果分裂航迹第3帧波门内有量测更新,如图1(a)所示,则以第2帧和第3帧的量测数据作为航迹头输出;②如果分裂航迹均未更新,则删除所有分裂航迹;③如果分裂航迹部分更新,则以部分更新航迹的第2帧与第3帧量测数据构成航迹头。如果出现航迹合成现象,同样需要利用第3帧数据来判决:①如果合成航迹第3帧波门内有量测更新,如图1(b)所示,则以第2帧和第3帧的量测数据作为航迹头输出;②如果合成航迹未被更新,则删除所有合成航迹。
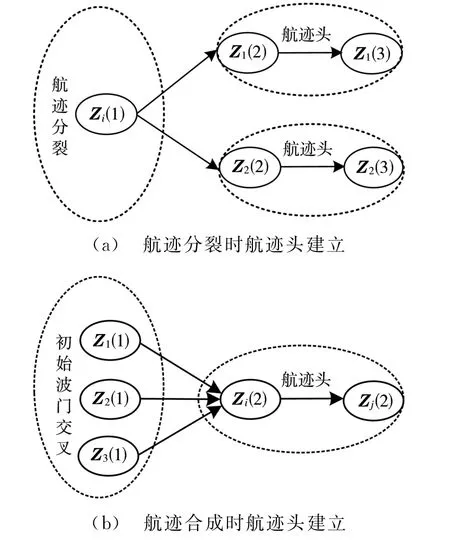
图1 延迟初始波门设计原理示意图
1.2 相关波门设计
1.2.1 基于角度约束的相关波门设计
基于角度约束的相关波门根据雷达的测量误差,在椭圆相关波门的基础上添加角度约束进一步剔除部分虚假量测来提高航迹起始成功率。假设第k+1时刻的第i个量测数据为Z i(k+1),第k时刻第j条临时航迹外推值为^Z j(k+1|k)。那么在线性高斯条件下,新息v ij(k+1)为
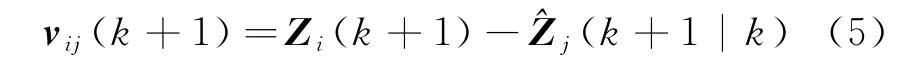
且服从高斯分布N[0,S(k+1)]。因而其归一化值
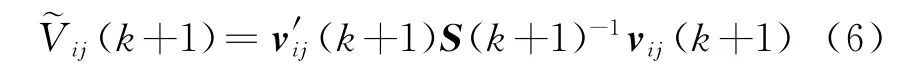
服从χ2分布。可以按χ2检验设置门限对进行统计检验。S(k+1)为新息协方差矩阵,可根据不同外推方法或经验设定[11]。
基于角度约束的自适应波门根据雷达测角误差,在椭圆波门的基础上增加角度约束,即

式中:θ(k+1),^θ(k+1|k)为k+1角度量测值与预测值;δθ为雷达测角误差标准差;kθ为χ2分布的参数平方根。
1.2.2 基于参数空间约束的相关波门设计
假设雷达在第k时刻和第k+1时刻量测数据的笛卡尔坐标为{(x k,y k),(x k+1,y k+1)}。通过Hough变换,将数据变换到参数空间{ρk(θ),据此,可构造参数空间中的差分函数:
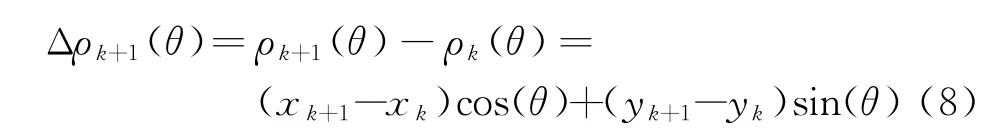
令Δρk+1(θ)=0,可得ρk+1(θ)和ρk(θ)过零交汇坐标

对目标航迹而言,过零交点θ0k+1和θ0k必须非常接近,即

σ0为判决门限。除此之外,差分函数提供了向量(x k+1-x k,y k+1-y k)的指向,修正的Hough变换要求处斜率的符号必须相同。

1.3 最大似然关联准则
假设第k+1时刻的量测数据Z(k+1),落入M(M>1)个临时航迹的相关波门相交区域内。记量测Z(k+1)来自临时航迹j的事件为

则其似然函数为
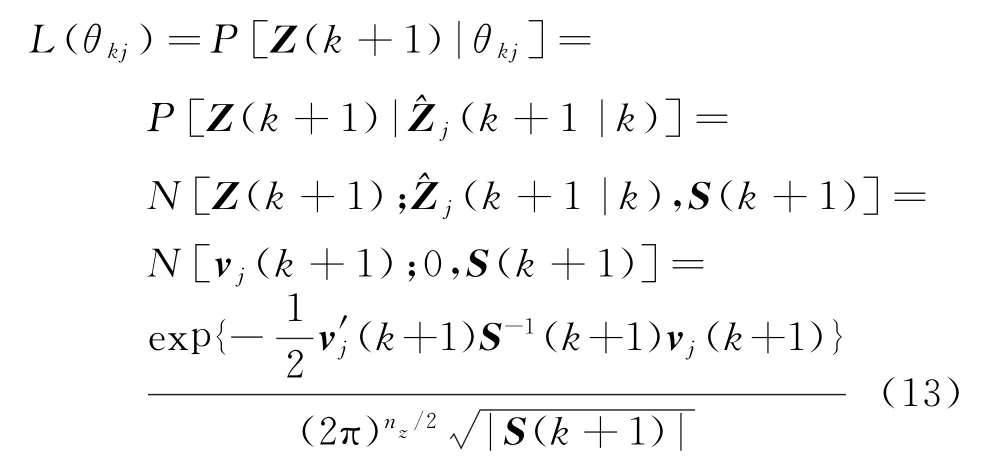
式中,v j(k+1)为量测新息,n z为量测维数,S(k+1)为新息协方差矩阵。最大似然的关联准则选取似然函数最大的临时航迹作为真实航迹,即
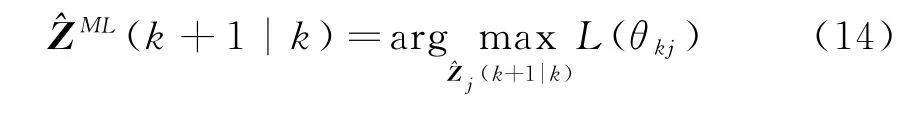
2 仿真与分析
为了说明算法的有效性,基于蒙特卡罗仿真本文引入如下评价指标。
1)正确航迹起始率PD
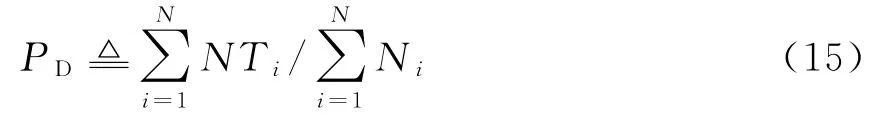
式中:N为蒙特卡罗仿真次数;NT i,N i分别为第i次仿真中真实航迹起始个数和真实目标航迹总数。
2)航迹起始虚假率PF

式中:NF i,NR i分别为第i次仿真中虚假航迹起始个数和起始航迹总数。
3)重复起批航迹数NC

式中,NC i为第i次仿真中重复起批航迹数。
假设雷达对50~60 km范围内的海域进行监视。区域中有多个匀速直线运动的舰船目标。仿真实验各参数设置如下:舰船目标的速度范围在5~30节;雷达扫描周期为10 s;雷达每帧接收的虚假量测在探测空间内呈均匀分布,数目服从均值为λ的泊松分布[12]。此外,为了简化问题,本文不考虑机载预警雷达载机运动效应和坐标转换,跟踪滤波器选择去偏转换卡尔曼滤波(CMKF)。图2给出了在雷达测距误差δr=50 m,雷达测角误差δθ=0.04°,λ=25,目标数目为10(其中有6个目标较为密集)时的仿真场景,其中雷达点迹数据为10帧。
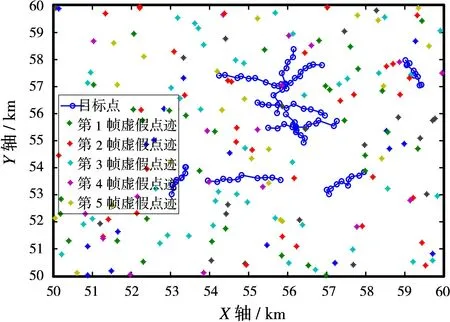
图2 海面多目标点迹仿真图
图3给出了海面舰船目标密集条件下,航迹起始算法的性能比较。仿真中,将本文所提算法(其中算法1采用基于角度约束的相关波门,算法2采用基于参数空间约束的相关波门)与HRM、LBM进行了对比。仿真中M/N的滑窗逻辑采用3/4准则。其中HRM、LBM使用5个周期的量测数据,改进算法使用6个周期点迹数据。

图3 航迹起始算法效果图
从图3可以看出,HRM起始了15条航迹,其中重复起始6批航迹;LBM起始了14条航迹,其中重复起始了3批航迹,错误起始1批。因而,HRM、LBM难以适用于海面密集多目标。算法1、算法2起始了10条航迹,无重复起和批虚假航迹。其性能优于传统算法。在相同仿真条件下,对航迹起始算法进行了50次蒙特卡洛仿真,仿真统计结果如表1所示。

表1 航迹起始算法统计结果
统计结果表明,在目标密集下,两种改进算法均能有效降低传统算法中的航迹重复起批现象,从而降低航迹起始虚假率。但两种改进算法的PD较LBM均有所降低,这是由于在解决航迹分裂与合成问题时,可能同时将真实目标航迹删除,因而要保证较高的PD需要更多周期的量测数据,航迹起始需要更长时间。改进算法2的正确航迹起始率PD高于改进算法1,这是由于修正的Hough变换能对近似线性目标进行有效检测,同时密集的目标环境及海杂波的影响使得算法2航迹起始虚假率PF高于算法1。
图4给出了不同测角误差背景下航迹起始算法的性能比较,雷达测角误差变化范围为[0.01°,0.1°],仿真中各算法的门限设置与实验1相同,实验进行了100次蒙特卡罗仿真。
仿真结果显示,随着雷达测角误差的起伏程度加大,4种算法的正确航迹起始率PD均降低,航迹起始虚假率PF均升高。改进算法2对测角误差表现出最好的鲁棒性。HRM、LBM、改进算法1的正确航迹起始率PD明显下降。由于LBM、改进算法1、改进算法2均采用相关波门统计判据,因此3种算法航迹起始虚假率PF对测角误差影响较为敏感。LBM、改进算法1、改进算法2的重复起批航迹数维持稳定,由于HRM的正确航迹起始率明显降低,很难起始真实目标航迹,其重复起批航迹数减少。
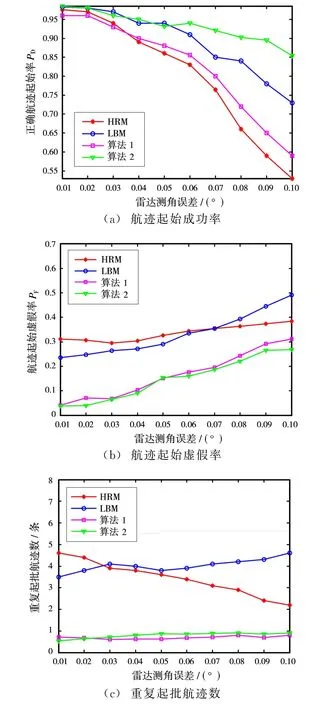
图4 不同测角误差条件下航迹起始算法性能比较
3 结束语
针对海面多目标航迹起始的特点,本文从初始波门设计、相关波门设计及关联准则环节入手,提出了一种适用于机载预警雷达海面多目标跟踪的航迹起始算法。仿真结果表明,所提算法在目标密集和量测噪声起伏条件下能有效起始海面舰船目标,具有较强的工程应用价值,同时也为海面多目标跟踪研究奠定了基础。
[1]BAR-SHALOM Y,FORTMANN T E.Tracking and Data Association[M].Boston:Academic Press,1988.
[2]BLACKMAN S S.Multiple-Target Tracking with Radar Applications[M].Norwood,MA:Artech House,1986.
[3]丁鹭飞,耿富录,陈建春.雷达原理[M].5版.北京:电子工业出版社,2014:308-312.
[4]朱自谦,胡士强.机载雷达多目标跟踪技术[M].北京:国防工业出版社,2013.
[5]韩崇昭,朱洪艳,段战胜,等.多源信息融合[M].2版.北京:清华大学出版社,2010:350-360.
[6]何友,修建娟,关欣,等.雷达数据处理及应用[M].3版.北京:电子工业出版社,2013.
[7]鹿传国,冯新喜,孔云波,等.基于形态学和Hough变换的航迹起始研究[J].兵工学报,2013,34(6):704-710.
[8]WOODFORD O J,PHAM M T,MAKI A,et al.Demisting the Hough Transform for 3D Shape Recognition and Registration[J].International Journal of Computer Vision,2014,106(3):332-341.
[9]董天发,易伟,李小龙,等.一种临近空间高超声速目标航迹起始算法[J].雷达科学与技术,2014,12(6):623-628.
[10]朱继红,徐本连,王飞,等.基于蚂蚁规则库的纯方位目标跟踪的航迹起始[J].控制与决策,2011,26(2):303-307,312.
[11]朱自谦.并行联合概率航迹起始逻辑[J].电子学报,2007,35(12):2421-2424.
[12]BAR-SHALOM Y,DAUM F,HUANG J.The Probabilistic Data Association Filter:Estimation in the Presence of Measurement Origin Uncertainty[J].IEEE Control Systems,2009,29(6):82-100.
