机电扫描天线阵列接收信号调制效应分析

谢洪森,周 鹏,迟志艳,朱春平

(1.海军航空工程学院青岛校区,山东青岛266041;2.海军航空兵学院,辽宁葫芦岛125001;3.中国人民解放军91395部队,北京102443)

0 引言

利用天线方向图的方向性在空域进行周期性的扫描,是雷达或目标获取角度参数的主要方式。就天线而言,要在空域形成动态的波束扫描,通常有两种方式:一是通过伺服系统和传动机构使天线反射面周期性机械转动,从而在空域形成动态的扫描波束,这种方式称之为机械扫描,其主要特点是系统设计简单,技术成熟,但机械运动惯性大,扫描速度低,如环视雷达、跟踪雷达等;二是电扫描,采用这种方式时天线反射体和馈源不进行机械运动,而是通过周期性地改变各个阵元的相位、频率或幅度等参量,实现天线的波束在空域中的周期扫描[1]。其主要特点是扫描速度高,波束控制灵活精确,但系统设计复杂,设备相对昂贵。

作为雷达系统的一个特殊种类——塔康(Tactical Air Navigation,TACAN)系统,即战术空中导航系统,它属于相位时间复合的航空近程无线电导航系统。系统利用天线方向图的周期性旋转和发射周期性基准脉冲,为飞机提供角度信息,利用发射询问脉冲为飞机提供距离信息。该系统可安装在机场、航路点、运动载体上,可为以导航台为中心,半径几百公里范围内的飞机或运载体提供导航服务,机动性和灵活性较高,特别适合军事应用[2]。

本文针对TACAN系统的一种特殊应用场合,其天线既存在机械扫描又实施电扫描方式情况下,首先对TACAN系统测角原理进行了简要分析,建立了TACAN系统接收信号模型,并对其频谱特性进行了分析,计算机仿真结果与理论分析相吻合,最后对TACAN系统性能进行了分析,给出了论文的结论。分析研究系统天线波束空域扫描的调制效应具有重要的现实意义。

1 TACAN测角原理及其接收信号模型

TACAN电扫天线采用若干个阵元均匀排列构成一个圆形阵列结构,通过控制各个阵元的馈电相位形成空域的周期性扫描波束。为了进一步改善俯仰方向上的测角性能,TACAN天线是由若干个层叠的圆周阵列构成。而对于存在水平方向的机械运动,层叠阵列的分析方法与单层陈列的分析结果是一致的,因此本文假定TACAN天线简化为单层圆周阵列构成。

目标要获得相对于TACAN的距离坐标,是通过向TACAN发射经过编码的询问脉冲,TACAN经过适当延迟向目标发射应答脉冲,目标通过分析应答脉冲的延迟判断相对TACAN的距离。而目标要获得相对于TACAN的角度坐标,则是通过测量TACAN发射的周期性脉冲和TACAN周期性旋转的波束进行位置的判定[2]。

TACAN天线水平方向图如图1(a)所示,其数学表达式可写为

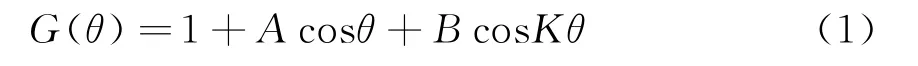
式中,A和B与阵元特性、天线结构以及馈电信号有关,K为一确定整数。该方向图在θ=0时存在一个最大值,在处存在极大值,一共有K个极大值。对TACAN而言,参数K=9。更为形象的解释是TACAN天线方向图是一个心脏形状(图1(a)虚线所示)上叠加9个瓣而已。如果该天线方向图进行水平周期性旋转,那么接收方将接收到一个类似AM调制的信号,假定天线方向图的旋转频率为那么接收信号中将存在2个非零点频,分别为Ω和KΩ。如果天线方向图在进行水平旋转的同时,还以频率为Ω发射定向基准脉冲,该脉冲的起始相位与天线方向图指向某个特定方向同步。这样接收机将接收信号的最大值与基准脉冲的相位差就可以判断出目标的相对位置,为了提高测角精度,还可以利用KΩ频率信号,得到更精确的测角精度[2]。对TACAN,Ω=30π。

要实现天线方向图的旋转,现以电扫TACAN为主要研究对象,其几何关系如图1(b)所示,接收机位于P点,某个阵元位于A点,Q为P点到XOY面的垂点,B和C分别是A点到线段OQ和OP的垂点。电扫天线是由Ne个阵元均匀排列构成的圆形阵列,要实现天线方向图以Ω速率旋转,则第n个阵元的馈电信号为

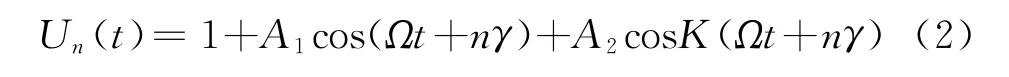
式中,A1和A2为调幅度,各阵元馈电信号初始相位TACAN接收机接收各个阵元发射的信号,其几何关系如图1(b)所示。接收信号经过包络检波后为

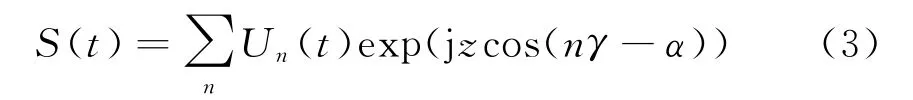
2 电扫描与机械扫描的调制效应分析

现在考虑一种特殊情况,就是图1(b)所示的圆形阵列以速率Φ匀速水平旋转,假定旋转方向满足笛卡儿坐标右手系方向。那么简单分析可知,接收信号将不仅受到馈电信号的影响,还可能受到阵列结构和旋转速率等多种因素的影响,而这些因素均有一个共同特征,即周期性,从而导致接收信号仍然是周期信号,其频谱由若干线谱构成。而TACAN测角主要依赖接收信号中的两个线谱分量的时域测量,为此必须充分研究接收信号的线谱扩展情况,才能对TACAN测角性能进行分析。

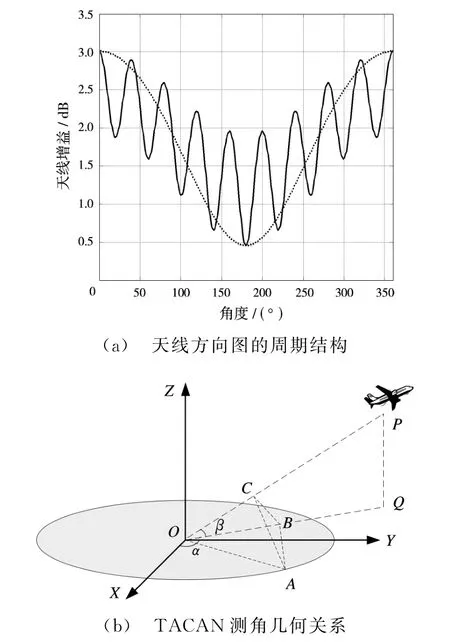
图1 TACAN测角原理

先讨论阵列结构对接收信号的影响问题。如图2所示,假定观测方向箭头所指方向,那么观测到的阵列结构存在两种状态,状态1如图2(a)所示,此状态表示某个阵元位于观测方向上,接收机可以同时接收到N+1个阵元发射的信号,考虑到对称性,N取偶数。显然该状态表现为离散形式,在阵列旋转一周的过程中,均匀出现Ne次。因此该状态的出现频率为旋转速率Φ的Ne倍。两个相邻的状态1之间的过程称之为状态2,该状态是一个连续的过程,在这个过程内接收机可以同时接收到N个阵元发射的信号。在阵列旋转一周的过程中,均匀出现Ne次,因此该状态出现的频率与状态1一样。有了这种概念,并结合式(3)可以初步分析阵列结构的周期旋转对信号周期性的影响[5]。假定起始时刻为图2(a)所示,假定1号阵元的馈电相位为0,经过时间T之后,m号阵元位于图2(a)所示的1号阵元位置,其馈电相位也为0,即

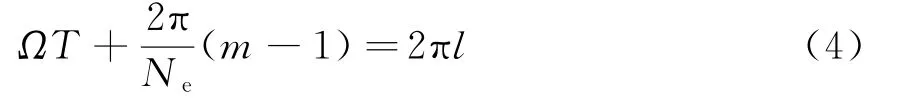
考虑到阵列的周期性旋转,时间T还满足:

综合式(4)和式(5),可以求得公共周期:

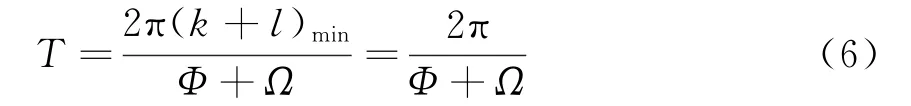
这说明接收信号的基准频率是馈电信号频率和阵列旋转频率的和。而对于TACAN系统而言,接收机接收的信号频率发生了改变将导致严重的性能恶化,解决的办法是改变馈电信号频率。仅仅分析其基本周期是不够的,这是因为接收信号是若干个基准周期整数倍的正弦信号叠加,接收信号的频率发生了周期延拓,频率分量可能发生交叠。为此必须进一步分析接收信号的数学模型。

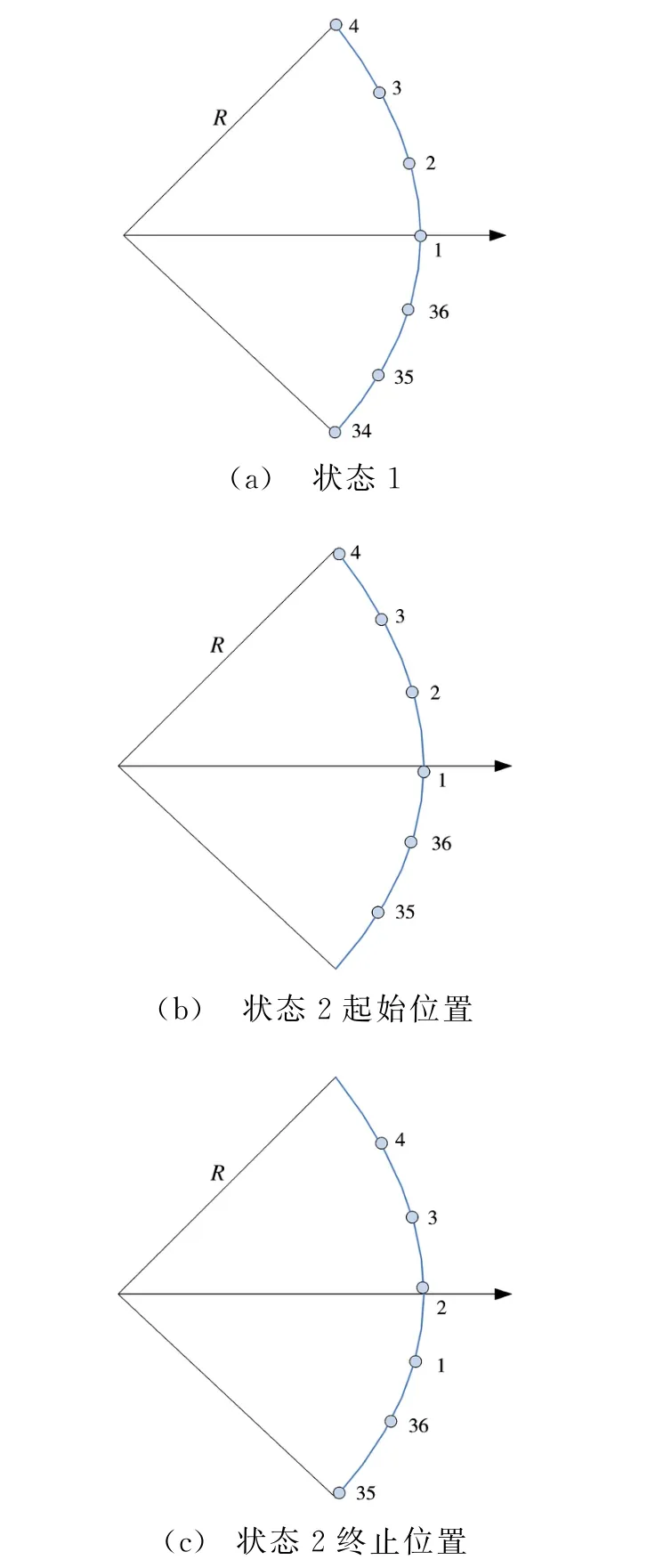
图2 观测方向上的阵列结构

为了简化分析,假定阵列馈电信号为相位调制的正弦信号,目标的方位角度为0。状态1是离散状态,因此在时域上表现为多个狄拉克函数的求和形式,阵列结构在状态1中保持不变,即求和公式中n的取值范围保持不变,且指数部分也保持不变,而馈电信号的相位却发生周期性变化[6],因此容易得到状态1时刻的接收信号可以表示为

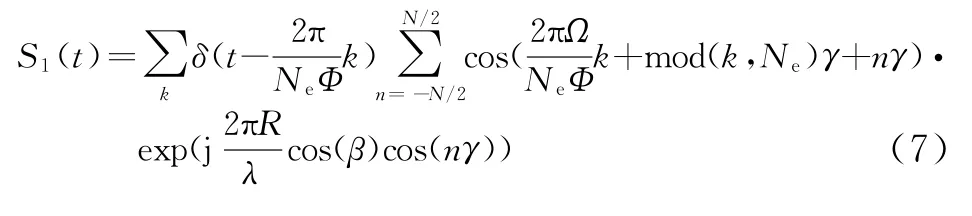
式中,mod表示取余算子。为了适合计算机仿真需要,需进行接收信号的数字化采样,而对于线谱信号,其采样率必须选择合适,否则容易出现频谱泄露问题。为此,假定状态2采样M-1个点,状态1对应一个采样点,那么采样率[7]可表示为

故状态1的接收信号数学模型可表示为

其中馈电信号相位中的取余算子并不需要[8],因此可进一步表示为

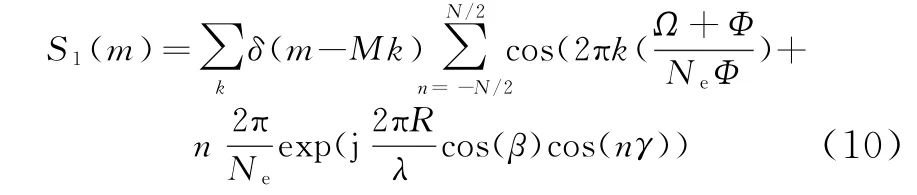
再分析状态2时的接收信号模型,如图2所示的状态2中,阵元个数始终为N个,因此求和范围与状态1不同,其次状态2为一个连续状态,因此其馈电信号的相位也是连续变化的,馈电相位的初始相位受到由于阵列旋转引入的阵列编号的变化。而指数部分在每个状态2中均是相同的:

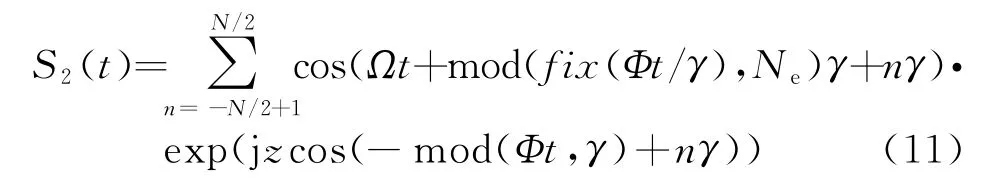
利用式(8)可得到数字信号模型:

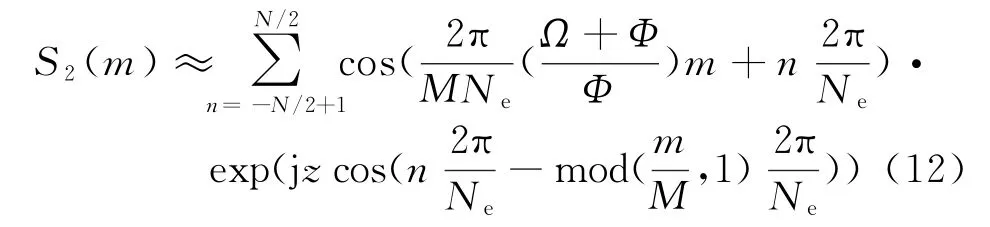
从式(12)可以看出,信号的基准周期与式(6)分析结论一致,其次考虑到旋转效应和阵列结构的周期性,状态2的周期性表现为频率发生了周期延拓,频率周期为

接收信号的数学模型可用式(10)和(12)进行完整表述。利用该模型可以得出这样的结论:当馈电信号频率为Ω,阵列旋转速率为Φ,那么接收信号的线谱位置为

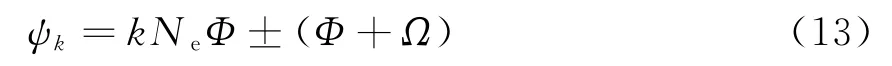
由此可见,接收信号的线谱结构发生了两个方面的畸变,一是基准频率不再是馈电信号的频率,而是加上了旋转速率,二是由于阵列的周期结构,导致了频率发生了周期延拓[8]。

除了考虑谱线出现的位置,还必须对谱线的强度进行分析。信号的周期性结构可以表示为

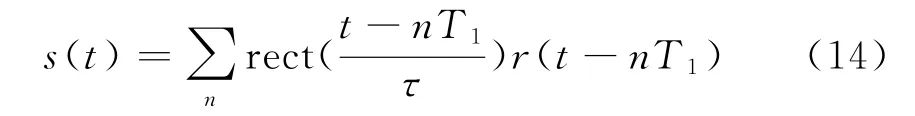
该信号是某个非周期信号r(t)的矩形窗截断后的周期扩展,接收信号的频谱就是r(t)的频谱与sinc函数的卷积后再进行频域抽样后的线谱构成,获得一个谱线幅度的闭合表达式比较困难,不过r(t)的频谱结构是一个低通函数,而sinc函数也是低通的,因此接收信号的线谱结构表现为随着阶数的增加而逐渐衰减的过程。也就是说,谱线扩展的阶数越高,其衰减越大。表1给出了3个点频的各阶扩展谱线的衰减程度。频率范围选择为0～180 Hz。从表1的数据可以看出,135 Hz谱线的各阶扩展分量衰减较小,其3阶和4阶扩展谱线出现在15 Hz附近,可能会对15 Hz信号的处理产生影响。

表1 各谱线衰减程度

3 调制效应的计算机仿真分析

依据前面讨论的信号模型,针对TACAN系统分析其接收机测角性能。由式(2)可知,发射信号中包含的调制信号频率分别为0,Ω,9Ω,这三种信号满足线性叠加原理,可以分别进行仿真和分析。假定天线阵列半径为1 m,阵列由36个阵元构成,观测阵元数目为6～7个。在进行数字仿真过程中,假定状态1与状态2共采样100个点,转速为1 Hz,馈电信号频率为14 Hz。

图3给出了各个阵元等幅同相馈电时,接收信号的波形及其频谱。接收信号的幅度表现为状态1和状态2交替,状态2持续的时间为转速的36倍。接收信号的频谱由若干线谱构成,分别为0,36,72,144等。

图4给出了当馈电信号为14 Hz,各个阵元相位相差10°,接收信号的时域和频域波形。从时域中可以看出,存在离散的脉冲信号,它是由于状态1引入的。频谱分析如式(13)分析结论一致。其中15 Hz信号是馈电信号频率14 Hz与转速1 Hz的和。21 Hz和51 Hz分别是36 Hz±15 Hz产生的。

图5给出了馈电信号如式(2)所示时,接收信号的时域和频域波形。可以看出,时域和频域波形均受到严重的破坏,时域波形不再是如图1(a)所示的规则信号,从信号的频域分析来看,其频谱谱线增加了,这是由于馈电的3个频率发生的周期延拓和交叠。一般而言,我们感兴趣的是接收信号15 Hz和135 Hz附近的线谱结构,而这些线谱结构显然最终影响了TACAN系统的测角性能。从图5可以看出,对于15 Hz的信号,其周围存在9 Hz和21 Hz的谱线,这两个谱线分别是36×4-135和36-15产生的,显然9 Hz的谱线是135 Hz谱线4阶扩展,因此其幅度低于有15 Hz的1阶扩展谱线21 Hz分量。再观察135 Hz附近的谱线,分别是129 Hz和144 Hz,它们分别是4×36-15和4×36产生的,显然129 Hz谱线是15 Hz谱线的4阶扩展,而144 Hz谱线是0 Hz的4阶扩展,因此这两个谱线的幅度相对较低。

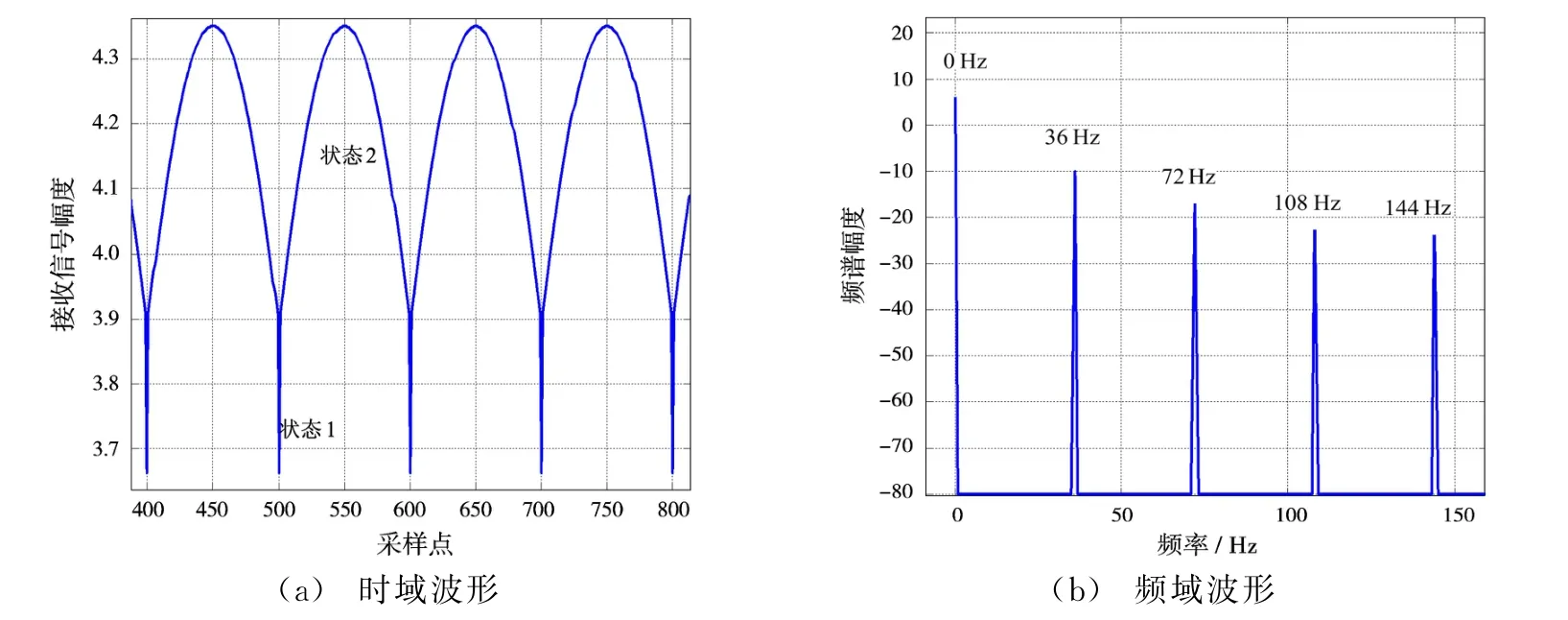
图3 等幅同相馈电时接收信号的时域频域波形

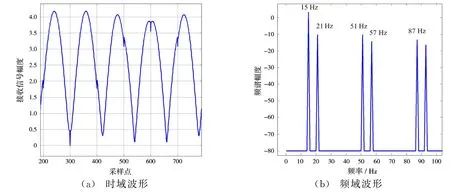
图4 等幅不同相位馈电时接收信号的时域频域波形

图5 TACAN接收信号的时域频域波形

4 调制效应对TACAN系统性能的影响分析

TACAN天线馈电信号包含3种线谱,即0频率,15 Hz和135 Hz。3种频率分量是线性叠加过程,因此针对每一个频谱成分均可以利用前述的数学模型进行分析。而考虑到TACAN系统的测角原理是对15 Hz信号和135 Hz信号的处理,为此利用前面的信号模型,重点分析15 Hz和135 Hz附近的谱线分量。

从前面分析可知,3种频率会产生周期扩展,而对于TACAN系统所关心的是15 Hz和135 Hz附近的谱线干扰。TACAN接收机采用的是15 Hz和135 Hz的窄带模拟滤波器,其带宽有一定的限制,当这两个频率分量附近存在其他谱线时可能会对其产生影响。

对于0频率,其谱线扩展的位置出现在:

假定转速为1 Hz,阵元个数为36,则在15 Hz最近的线谱分量为0阶扩展0 Hz和1阶扩展36 Hz,对135 Hz最近的谱线为3阶扩展分量108 Hz和4阶扩展分量144 Hz。对于15 Hz分量,其主要影响到135 Hz的谱线为3阶扩展分量123 Hz,4阶扩展分量129 Hz和159 Hz。135 Hz分量对15 Hz谱线的影响为3阶扩展分量27 Hz,4阶扩展分量9 Hz。

以上分析仅对某种一定情况而言,如果阵元个数发生改变,或者阵列旋转速度发生改变,前面的分析结果要发生相应的改变。一般而言,转速越大,低阶谱线扩展分量的影响就越大,例如若转速提高到4倍,则135 Hz的1阶扩展分量就会出现在9 Hz上,从而会增加对15 Hz信号的干扰。其次是当某些特定的转速时,可能会发生某阶扩展谱线分量出现的15 Hz或135 Hz分量上,如当其他条件不变,转速为10/3 Hz,容易分析出,135 Hz的1阶扩展分量出现在15 Hz上,由于相位的差异,会导致15 Hz信号分量发生畸变。

考虑到谱线的位置是已知的,可以设计合理的滤波器实现15 Hz谱线和135 Hz谱线的提取。由于接收信号的频谱宽度受到接收机带宽的限制,故15 Hz通道的输出频谱只含有15 Hz及其附近的谱线,135 Hz通道的输出只含有135 Hz及其附近的谱线。设计一个含有对应零点的FIR滤波器就可将这些位置已知的谱线加以滤除。滤波器的幅频响应如图6所示,其设计方法是将15 Hz或135 Hz附近的已知谱线位置作为滤波器幅频响应的零点,从而能够有效抑制干扰信号的影响。

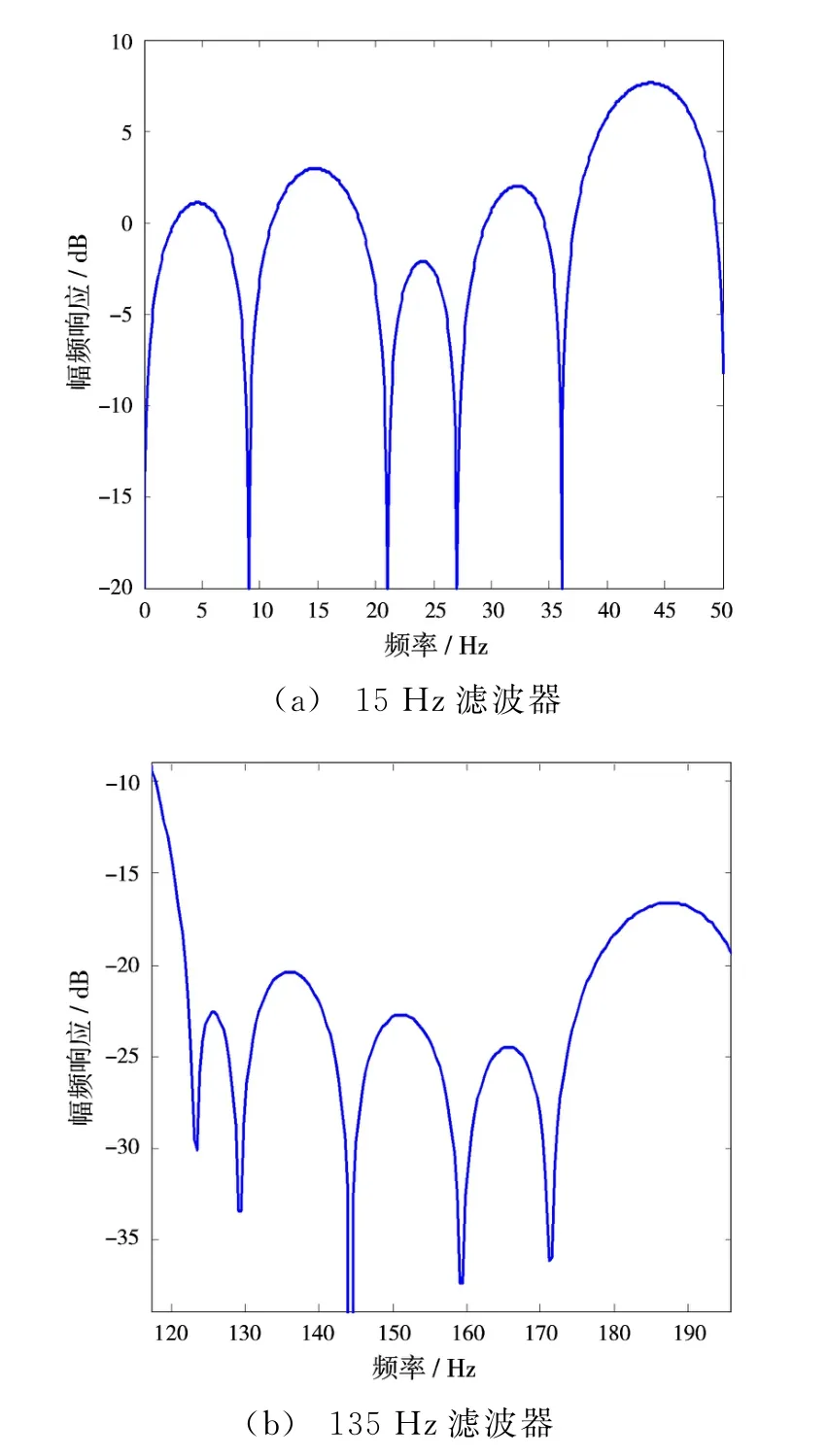
图6 滤波器幅频响应

5 结束语

天线波束的空域扫描方式包括电扫描和机械扫描。本文以TACAN系统为研究对象,在天线阵列实施电扫描同时存在阵列的机械旋转运动时,给出了接收信号的数学模型。经理论推导和计算机仿真结果表明,接收信号的频率是馈电信号频率与转速频率的和,其谱线发生了周期性扩展。针对这种情况,通过设计合理的数字滤波器可以抵消谱线扩展引入的接收信号失真问题。研究还表明,当转速处于某些特定频率时,扩展的谱线之间会发生交叠现象,可能会对TACAN系统测角产生不良影响,其影响的量化分析需进一步研究。其次,阵列的机械旋转速率可能存在不稳定的情况,表现在接收信号的谱线发生抖动或展宽,因此必须采用自适应滤波器替代原先的FIR滤波器。

[1]吴德伟.航空无线电导航系统[M].北京:电子工业出版社,2010:61-67.

[2]谢洪森.舰载机着舰无线电引导关键技术研究[D].烟台:海军航空工程学院,2012:8-11.

[3]彭政谕.阵列天线波束赋形技术研究与应用[D].杭州:浙江大学,2014:35-38.

[4]戴幻尧,李永祯,陈志杰,等.电扫偶极子相控阵天线的空域极化特性分析[J].国防科技大学学报,2010,32(1):84-89.

[5]赵万春,师君.圆形阵列天线方向图的分布函数优化方法[J].电讯技术,2010,50(7):91-96.

[6]葛佩,李明,刘翔.一种低旁瓣子阵线自适应波束形成方法[J].雷达科学与技术,2012,10(5):519-523.GE Pei,LI Ming,LIU Xiang.An Adaptive Beamforming Method at Subarray Level for Planar Array with Low Sidelobes[J].Radar Science and Technology,2012,10(5):519-523.(in Chinese)

[7]CHEN K,YUN X,HE Z,et al.Synthesis of Sparse Planar Arrays Using Modified Real Genetic Algorithm[J].IEEE Trans on Antennas and Propagation,2007,55(4):1067-1073.

[8]WILSON M J,MCHUGH R.Sparse-Periodic Hybrid Array Beamformer[J].IET Radar,Sonar and Navigation,2007,1(2):116-123.