镜像反转DMFT抛物方程算法∗

(海军航空工程学院信号与信息处理山东省重点实验室,山东烟台264001)

0 引言

刃峰是一种特殊的不规则地形,对空间电磁波传播特性会产生显著的影响。借助相应的算法可以实现对电波传播特性的预测,为雷达设计提供技术支持,针对刃峰条件下电磁波传播特性研究,已经取得了一些积极的成果,例如双向抛物方程算法,该算法在前向传播波基础上增加了对后向传播波的计算,最早应用于水下声场的传播特性预测[1]。后来Oraizi[2]第一个将其应用于电磁场在多刃峰环境下的传播计算,Ozgun[3]最早将其应用于大气波导条件下刃峰环境对电波传播特性的影响分析。随后该算法逐渐被应用于不规则地形且非均匀折射大气条件下的电波传播计算中[4-6]。

双向抛物方程虽然考虑了后向传播波的计算,但在算法实现上还存在很大的简化空间。以目前预测效率最高的DMFT抛物方程算法为例,该算法是一种考虑了边界阻抗条件的抛物方程快速数值算法[7-8],由于该算法建立在迭代运算基础之上,所以在特定的刃峰处计算地形遮蔽效应[9]引起的后向反射就不得不中断前向DMFT步进计算,转而启动后向DMFT算法[10-11],对于多刃峰环境,势必大幅增加算法复杂度。基于此种考虑,本文提出一种镜像反转DMFT算法,简化了算法程序上的复杂度,并通过理论推导,证明了该算法与双向DMFT算法是等效的,在此基础上计算刃峰环境下的电波传播损耗分布。

1 镜像反转DMFT抛物方程算法

1.1 问题描述

以单刃峰环境为例,设天线位于高度ha,水平位置x=0处,由天线发射的电磁波前向传播至刃峰所在水平位置x=x0处,假设刃峰峰面为良导体。相应地,电磁波会因刃峰遮蔽而发生反射,前向传播的电磁波随即分解为前向传播波和后向反射波。假设由天线传播至x=x0处垂直剖面上的电磁场分布为ψ(x0,z),则对应的前向传播波和后向反射波分别为

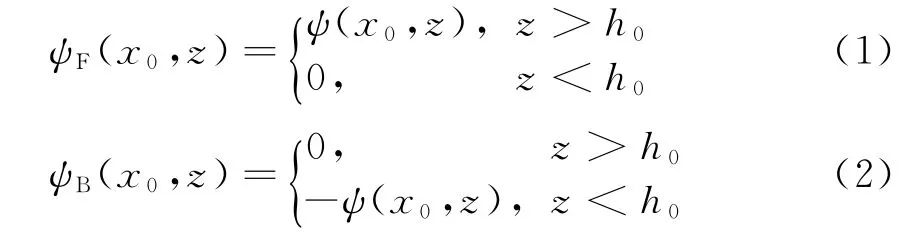
后向反射波以ψB(x0,z)为初始场,经后向DMFT抛物方程步进计算获得天线至刃峰间的反射场ψB(x,z),其中x=x0-Δx,x0-2Δx,…,0,将前后向传播波叠加,即求得整个计算空间内的场分布。

1.2 算法描述

定义电磁波沿+x和-x方向传播的衰减函数分别为uF(x,z)=e-ikxψF(x,z)和uB(x,z)= eikxψB(x,z),当电磁波沿+x方向传播至刃峰位置x=x0时,参考式(1)和式(2),获得前向传播的衰减函数和镜像传播的衰减函数分别为

x＞x0区间的场分布由uF(x0,z)经前向DMFT抛物方程算法步进计算获得:

假设天线到刃峰间基于抛物方程的水平方向步进数目为N,即x0=N·Δx,其中Δx为水平方向步进的长度,对镜像传播场的衰减函数uM(x0,z)执行N步前向DMFT抛物方程步进计算,分别求得uM(x0+Δx,z),uM(x0+2Δx,z),…,uM(x0+ NΔx,z)。该镜像场实际并不存在,完全由数值计算虚拟获得。

基于上述计算,在x-z二维笛卡尔坐标系中以x=x0为对称轴,对x＞x0处的镜像场作镜像反转:

将式(6)求得的反转镜像场作距离因子加权,即得x＜x0区间内的反射场:

综合式(3)～(7),给出单刃峰环境下基于镜像反转的DMFT抛物方程算法:

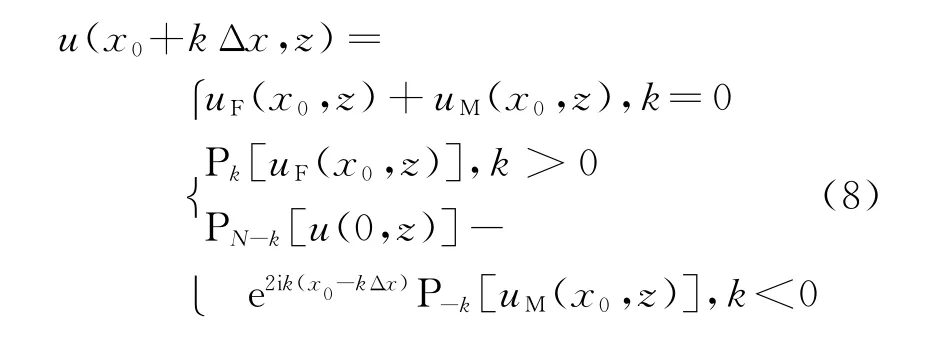
式中,P表示前向DMFT抛物方程的步进计算函数,下标表示执行前向DMFT抛物方程的步进计算的步数,k取整数。

2 算法性能理论分析

假设在大气折射率为n(x,z)的各向同性介质中电磁波传播的二维标量波动方程为

设式中解的形式为ψ(x,z)=u(x,z)eik0x,将其代入式(9),整理可得

引入伪微分算子:

则式(10)可因式分解为

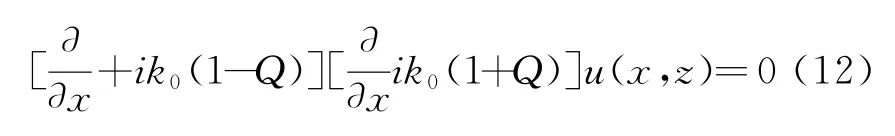
式中,前向传播项为

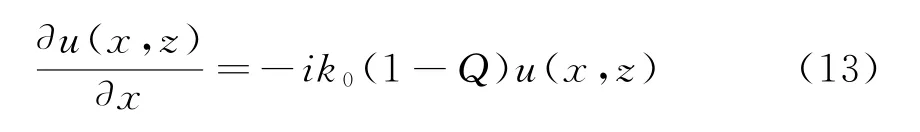
后向传播项为

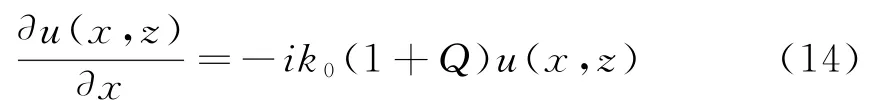
若给定u(x0,z),则前向步进上的解为

参考相关文献,假设电磁波传播过程中于水平位置x0处遇刃峰遮蔽,峰顶高度为h0,设由辐射源前向传播至该步进处的电磁场为ψ(x0,z),则由该步进上电磁场形成的前向传播场和因刃峰屏蔽而形成的后向传播初始场分别为

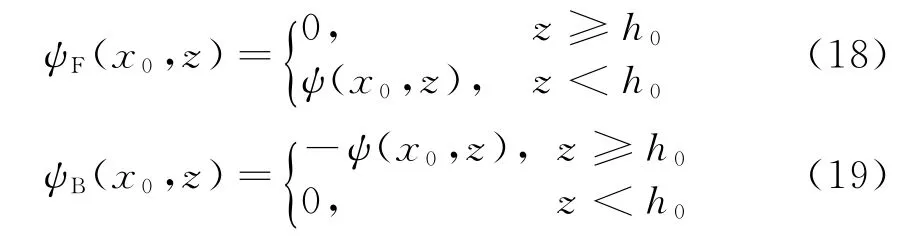
由于前向场和后向场的解分别具有如下形式:

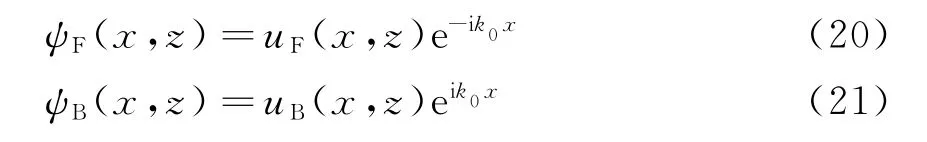
故后向传播场的解与前向传播场的解满足如下关系:

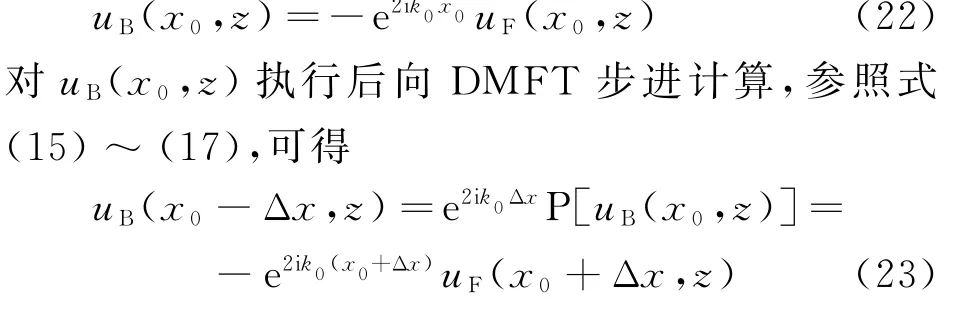
以上理论分析证明,该算法与双向DMFT抛物方程算法在理论上是等效的,刃峰遮蔽效应产生的后向反射场可由前向DMFT抛物方程步进计算获得,只需将所得结果在刃峰处作镜像反转并进行相应距离上复指数因子的加权,该算法的优势在于无须调用后向DMFT算法,在前向DMFT迭代计算过程中即可同步完成后向反射场的计算。在多刃峰情形下,可迭次调用该算法计算刃峰间的多次反射场,特别需要指出的是,虽然本文对该算法的理论推导是在水平均匀大气折射条件下进行的,但该算法同样适用于水平非均匀大气折射条件下的电波传播计算,只需将反射距离区间的大气折射率数据镜像加载到前向传播区间即可。

3 算法仿真与结果分析

为检验本文算法计算反射场的性能,设雷达发射天线高度为120 m,发射频率为1.8 GHz,天线极化方式为水平极化,天线3 dB波束宽度为15°,天线类型为高斯天线,距天线水平方向40 km处有一刃峰,高度为80 m,下边界为光滑海面,结合本文算法,双向DMFT算法和传统的前向DMFT算法分别计算标准大气条件下距离天线水平距离30 km处电磁波传播因子垂直剖面,结果如图1所示。由图1对比本文算法与双向DMFT算法给出的传播因子垂直剖面,两者在高度区间的上半部分拟合较好,由于两种算法地物反射的机器运算存在数值差异,在高度区间的下半部分结果略有出入,但偏差并不大。传统的前向DMFT算法给出的传播因子垂直剖面在高度区间的上半部分也能较好地拟合双向DMFT算法给出的结果,但相对本文算法的拟合效果,其在下半部分拟合偏差明显较大,这是由于传统的前向DMFT算法完全忽略了刃峰引起的反射。同时,图1也反映了刃峰引起的反射效应主要发生在刃峰峰尖以下及附近的高度范围内。

图1 距天线30 km处传播因子垂直剖面

在标准大气条件下,计算电波传播损耗的二维空间分布,如图2所示。对照图3所示无刃峰环境下的电波传播损耗分布,可见水平方向0～40 km区间内由于刃峰的遮蔽效应发生了电磁波的反射,40～120 km区间内的电波传播损耗分布也因刃峰的遮蔽效应发生了明显的变化。其中,刃峰背面明显出现损耗高于150 d B的区域,进一步对照图4所示双刃峰环境下的电波传播损耗分布,可明显观察到随着电磁波继续前向传播,遇第二个刃峰遮蔽发生反射,该反射波又在第一个刃峰背面发生二次反射,第二个刃峰背面出现面积更大的损耗高于150 dB的区域。电磁波绕过第二个刃峰后在水平方向距天线80 km以外的低空区域再度形成损耗较周围区域低的传输通道。

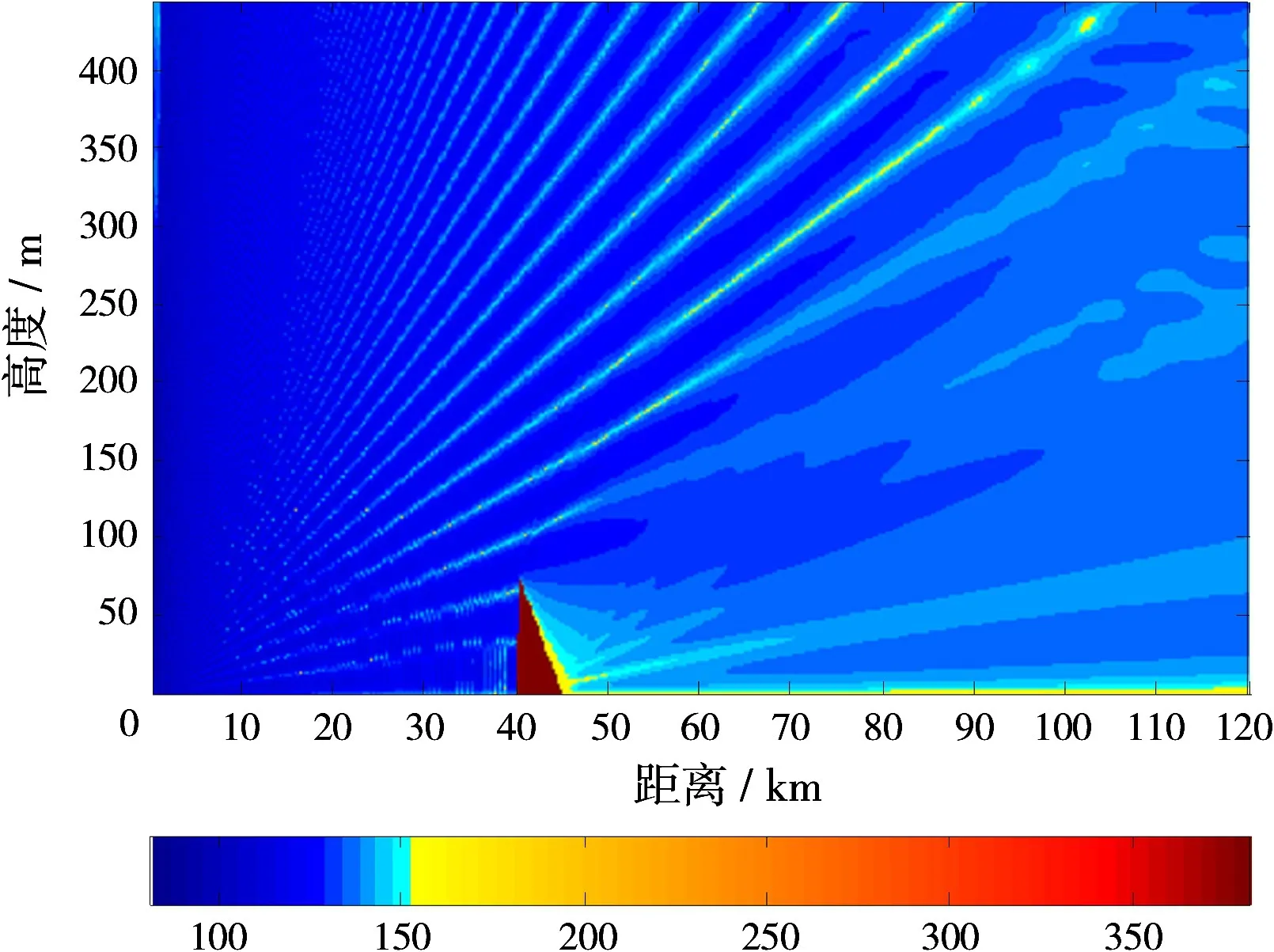
图2 单刃峰环境下的电波传播损耗

图3 无刃峰环境下的电波传播损耗

图4 双刃峰环境下的电波传播损耗

4 结束语

刃峰引起的电波反射会严重影响电波传播特性的预测精度,基于电波传播波动方程的后向传播因式,传统的双向DMFT抛物方程算法采用后向DMFT算法计算反射场,算法精度较高,但在峰面处需中断前向DMFT迭代计算,转而调用后向DMFT算法,无法将两者并行处理,增加了计算流程上的复杂度。本文提出的基于镜像反转的DMFT抛物方程算法将峰面前侧的地形及大气折射率信息加载于峰面镜像方向,借助镜像反转的方法,无须调用后向DMFT算法,即可同步计算前向传播波和峰面反射波。该算法可计算单刃峰或多刃峰环境中非均匀大气折射条件下的电磁波传播。本文通过对抛物方程的理论推导,证明了该算法与传统的双向DMFT算法在理论上是等效的,虽然两种算法对地物反射的机器运算一定程度上存在数值差异,但计算结果偏差并不明显,总之,本文算法在不明显改变算法有效性和可靠性的前提下提高了算法的实用性。

[1]COLLINS M D,EVANS R B.A Two-Way Parabolic Equation for Acoustic Backscattering in the Ocean[J]. Journal of the Acoustical Society of America,1992, 91(3):1357-1368.

[2]ORAIZI H,HOSSEINZADEH S.Radio-Wave-Propagation Modeling in the Presence of Multiple Knife Edges by Bidirectional Parabolic-Equation Method[J]. IEEE Trans on Vehicular Technology,2007,56(3): 1033-1040.

[3]OZGUN O.Recursive Two-Way Parabolic Equation Approach for Modeling Terrain Effects in Tropospheric Propagation[J].IEEE Trans on Antennas and Propagation,2009,57(9):2706-2714.

[4]SALSKI B,CELUCH M.On the Equivalence Between the Maxwell-Garnett Mixing Rule and the Debye Relaxation Formula[J].IEEE Trans on Microwave Theory and Techniques,2012,60(8):2352-2358.

[5]KADDOURI I,TENIOU D E.Inverse Problem for a Nonlinear Parabolic Equation with Nonsmooth Periodic Coefficients[J].SeMA Journal,2014,66(1):55-69.

[6]MIRET D,SORIANO G,NOUGUIER F,et al.Sea Surface Microwave Scattering at Extreme Grazing Angle:Numerical Investigation of the Doppler Shift[J]. IEEE Trans on Geoscience and Remote Sensing, 2014,52(11):7120-7129.

[7]KARIMIAN A,YARDIM C,GERSTOFT P,et al. Multiple Grazing Angle Sea Clutter Modeling[J]. IEEE Trans on Antennas and Propagation,2012,60 (9):4408-4417.

[8]KARIMIAN A,YARDIM C,HODGKISS W S,et al.Estimation of Radio Refractivity Using a Multiple Angle Clutter Model[J].Radio Science,2012,47 (RS0M07):1-9.

[9]徐源,陈伯孝.地形对基于波瓣分裂的米波雷达测高方法的影响[J].雷达科学与技术,2008,6(1):9-14.

[10]李德鑫,杨日杰,王元诚,等.不规则地形条件下双向DMFT电波传播特性算法研究[J].航空学报, 2012,33(2):297-305.

[11]李德鑫,杨日杰,官巍,等.不规则地形条件下的双向抛物方程模型研究[J].宇航学报,2012,33(2): 235-241.