基于动态规划理论的改进型价值迭代算法∗

(电子科技大学电子工程学院,四川成都611731)

0 引言

随着无线电测量技术的不断发展,雷达技术也迈上了一个新的台阶[1-2]。传统的雷达利用回波信号分析目标的特性,这样的探测方式被动,无法体现雷达的空间认知能力。于是,有人提出了认知雷达的概念。认知雷达是一种能够根据回波信号认识环境状态的雷达。它通过对回波信号的分析,提取出环境信息并动态地改变发射波形,以达到更高的目标分辨率。而认知雷达的核心便在于其智能化,它能自适应地学习认知环境,并能根据环境的变化而作出调整[3-5]。这种能力的高低需要依靠准确而快速的自适应算法来支撑。这样,提高自适应算法的计算速度和准确度则是在提高宽带认知雷达的认知能力,所以研究宽带认知雷达的自适应波形选择算法有着重要的意义。策略迭代算法、价值迭代算法、Q学习算法都是当前比较流行的自适应算法,它们都是基于动态规划理论,而动态规划理论的核心思想来源于贝尔曼最优准则[6-7]。故本文将基于动态规划理论及其核心思想贝尔曼最优准则,讨论一种改进型的价值迭代算法,并通过仿真比较它与其他算法的优劣。

1 动态规划算法

动态规划算法是基于贝尔曼最优准则,在马尔科夫决策模型下提出的。马尔科夫理论为动态规划算法提供了选择决策序列的数学理论基础,而贝尔曼最优准则为其提供了选择最优策略的数学代价函数。两者共同奠定了动态规划算法的基础[8-10]。

1.1 马尔科夫决策模型

图1表示了马尔科夫决策装置与环境交互图,图中,对于任意给定的状态i,可以选择的动作u ik(就是决策装置产生的对环境的输入)集合用U={u ik}表示。其中u ik意味着在i状态下有k个动作可以选择。不同的动作作用于环境,将产生不同的下一状态j,而环境从i状态转移到j状态的概率完全由当前状态i和当前动作u ik决定,这个特性就是马尔科夫特性。它表明决策装置采取哪一动作可以从当前状态中获取信息,并根据当前状态决定。同时,在i状态下,若能确定下一状态,则可以选择合适的动作与之匹配,这便与认知雷达的波形选择联系起来了。这样,动作的选择便成为了关键点。根据图中的模型,在状态i时,当采取动作u ik而转移到状态j时,状态将反馈给决策装置一个报酬λnr(i,u ik,j),其中,λ为折扣因子(0＜λ＜1),r(i,u ik,j)表示状态从i转移到状态j的过程中,采取动作u ik而获得的报酬。

图1 马尔科夫过程模型

1.2 贝尔曼最优准则

现在考虑雷达实际的环境状态,由于雷达测量目标的实际状态是有限的,本文将它定为K,即雷达环境共有K个状态。本文重新定义报酬函数为r(X n,u n(X n),X n+1),表示状态从X n到状态X n+1所获得的报酬。对于一个K状态的动态规划问题,本文定义

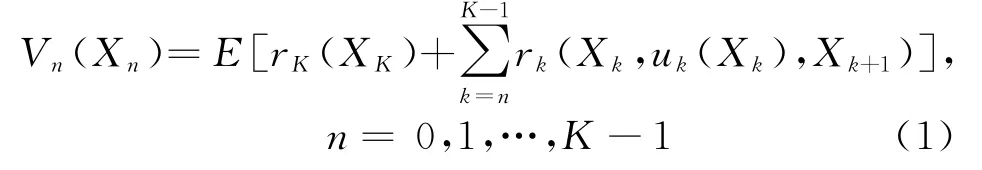
式中,V n(X n)代表总期望报酬。若策略π={u k}为最优策略,那么,在π={u k}时,

即此时π使得总期望报酬在n时刻以后的值达到最大,对于n时刻以后的所有子问题,π都为最优策略;若π不为最优策略,那么,当状态发生转移时,以后子问题所选择的最优策略将增大V n(X n)的值,这样通过对n时刻后每一时刻状态的报酬值进行迭代更新后,将确定出一个满足所有状态最优策略。这便是贝尔曼最优准则。

1.3 动态规划算法

根据以上的叙述,现在本文将动态规划算法描述如下:该算法从K-1到0时刻反向进行动态规划。假设π={u k},那么对于n=0,1,…,K-1,式(1)的最优表达式即为

对于一个策略π,现在重新定义报酬函数

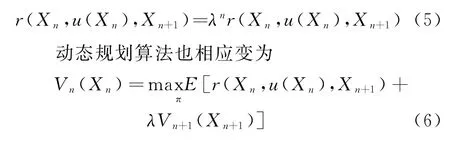
令当前状态X n=i,下一状态X n+1=j,则式(6)可以表示为

将式(7)写成概率形式为

每一个状态都对应了一个最优贝尔曼方程,一共有N个方程,所有状态的最优贝尔曼方程联立求解后得到的π={u k}即为最优策略。

2 价值迭代算法及改进的价值迭代算法

计算最优策略的方法一般有策略迭代算法和常规价值迭代算法[11],现在分别加以讨论。

2.1 策略迭代算法

策略迭代的基本思想是任意选择一个策略开始,不断迭代,直到不再有更好的策略出现为止。基本步骤如下:

步骤1 估值阶段:此阶段中,本文随机选择一个策略uk(i),用贝尔曼最优方程计算其价值函数mk(i),随后进入步骤2。其中

步骤2 策略改进阶段:此阶段,利用步骤1中的价值函数值得到一个更好的策略uk+1(i)。

步骤3 如果步骤1和步骤2中的策略完全相同,即uk+1(i)=uk(i)对于每一个状态i都成立,那么,停止迭代。否则,反复执行步骤1、步骤2,直到uk+1(i)=uk(i)出现。

2.2 常规价值迭代算法

价值迭代算法是一种不断近似于最优方案的算法,因为它不断利用贝尔曼最优方程更新,最终得到一个最优的价值函数[12-13]。根据1.3节中的讨论,贝尔曼最优方程如下:

式中,S为状态空间,U为波形控制变量集合。

价值迭代最基本的思想就是,先将价值向量Vn(i)赋予初值,然后再用贝尔曼最优方程即式(11)进行不断的迭代更新,更新过程中,Vn(i)的值会趋近于一个固定值。如果这种迭代不断进行下去,那么Vn(i)的值就会在某一时刻达到这个固定值,此值即为最大的价值。但是,通常认为当Vn(i)的值非常接近该固定值时,即可认为该值即为接近最优价值的次优近似值。此时,便可以停止迭代,减少算法的计算量。现在给出价值迭代算法的终止条件:

式中,δ为一很小的控制量,用来控制前后迭代价值的接近程度,λ为式(11)中的折扣因子。式(12)表明,当前后迭代价值即Vn+1(i)与Vn(i)的差别小于δ(1-λ)/2λ时,即停止迭代。

下面给出常规价值迭代的算法步骤:

步骤1初始化所有的V(i),令k=0,设定δ, δ为大于0的常数;

步骤2 对于每一个i∈S,计算

步骤3 如果当前

成立,则转移到步骤4,否则,令k=k+1,返回到步骤2,继续迭代;

步骤4 对于每一个i∈S,选择

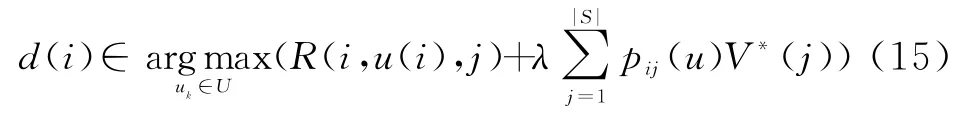
此时停止迭代,得到最优策略d∗(i)。

步骤3中‖Vk(i)-Vk+1(i)‖的值每一次迭代都会下降,直到其下于门限值时,迭代停止。并且需要指出,该算法是针对所有的i∈S,故每一个状态都要完成以上每一个步骤。由于常规价值迭代算法需要应用到实际的雷达工作环境中去,所以考虑到实际环境中,该算法并不是最优的。因为该算法运算速度慢,收敛时需要的迭代次数多,这样便降低了雷达的自适应能力和应变环境变化的能力,所以现在提出一种改进型的价值迭代算法。

2.3 一种改进的价值迭代算法

在常规的价值迭代算法中,计算当前迭代的价值函数时,需要将以前已经计算过的状态空间中的状态又计算一遍,这样便加大了计算的复杂度[14]。改进价值迭代算法便是针对这一缺点而提出。当状态为i时,已经计算出了Vk+1(i′),其中i′=1,2,…,i-1,此时,可以将已经计算得出的状态的函数价值Vk+1(i′)来代替Vk(i′),从而避免了重复计算,提高了算法的收敛速度。这种价值迭代算法的收敛速度更快,对环境的变化适应能力也越强。

下面给出改进价值迭代的算法步骤:

步骤1初始化所有的V(i),令k=0,设定δ,δ为大于0的常数;

步骤2 对于每一个i∈S,计算

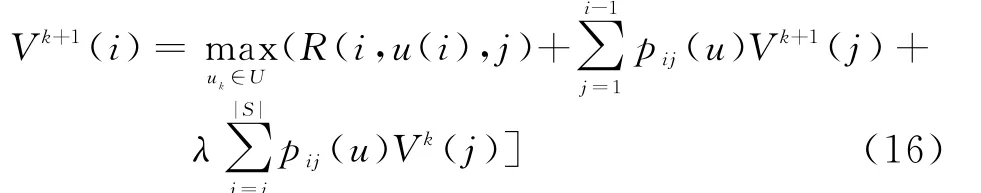
步骤3 如果当前

成立,则转移到步骤4,否则,令k=k+1,返回到步骤2,继续迭代;

步骤4 对于每一个i∈S,选择

此时停止迭代,得到最优策略d∗(i)。

2.4 现在已有的改进价值迭代算法

目前,雷达领域已经拥有几类改进价值迭代算法,如Gauss Siedel价值迭代算法、相对价值迭代算法以及跨度半-范数判决准则价值迭代算法。这些算法在某一方面都有所改进,但是工程应用实践性不强。下面,本文将对其中几种算法的原理加以讨论,并与本文的算法进行比较。

(1)相对价值迭代算法

相对价值迭代算法是当前已经被提出的一种改进型价值迭代算法,该算法利用当前已知的状态情况所产生的价值作为基准,并用当前情况的价值相对于已知状态价值的差距作为下一状态的更新依据,对于不含有折扣因子λ时,更新速度很快。然而,实际的雷达环境是需要折扣报酬λ的,所以,此方法不适用于实践环境。

(2)跨度半-范数判决准则价值迭代算法

此算法的优越性在于提高了前后状态的判决准确度,即使用半-范数准则代替了常规价值迭代算法的步骤3作为判决方式。这样做使得算法在判决的准确度上提高了一个层次,但并未在提高更新速度上产生积极效果,雷达依然需要经过大量的计算才能确定发射波形,所以不适应于雷达响应速度的要求。而本文所述算法与其相比的优势正是在于计算量小,更新速度快。

综上所述,本文所提价值迭代算法在波形选择的准确性上虽略显不足,但其快速的更新速度减轻了雷达的计算量,更加适用于实际环境。故本文所提算法不失为一种实际适应能力更强的算法。

2.5 雷达波形选择的数学建模

雷达对波形的选择主要依靠不同波形产生的价值V(i)来决定。如图2所示,在同一环境情况下,选择能使目标价值达到最大的波形作为最优波形。设定环境空间为X(x∈X),雷达波形库为U(u∈U),目标报酬为R(p k,u k,p k+1)。雷达通过对环境的学习将波形库中的波形与目标环境对应起来,建立一一对应的关系即(x,u)集合,每一个状态x都会有一个最优波形u与之对应。这样,当雷达遇到已知环境时,便可以通过波形库中的对应关系选择出合适的波形,达到自适应波形选择的目的。

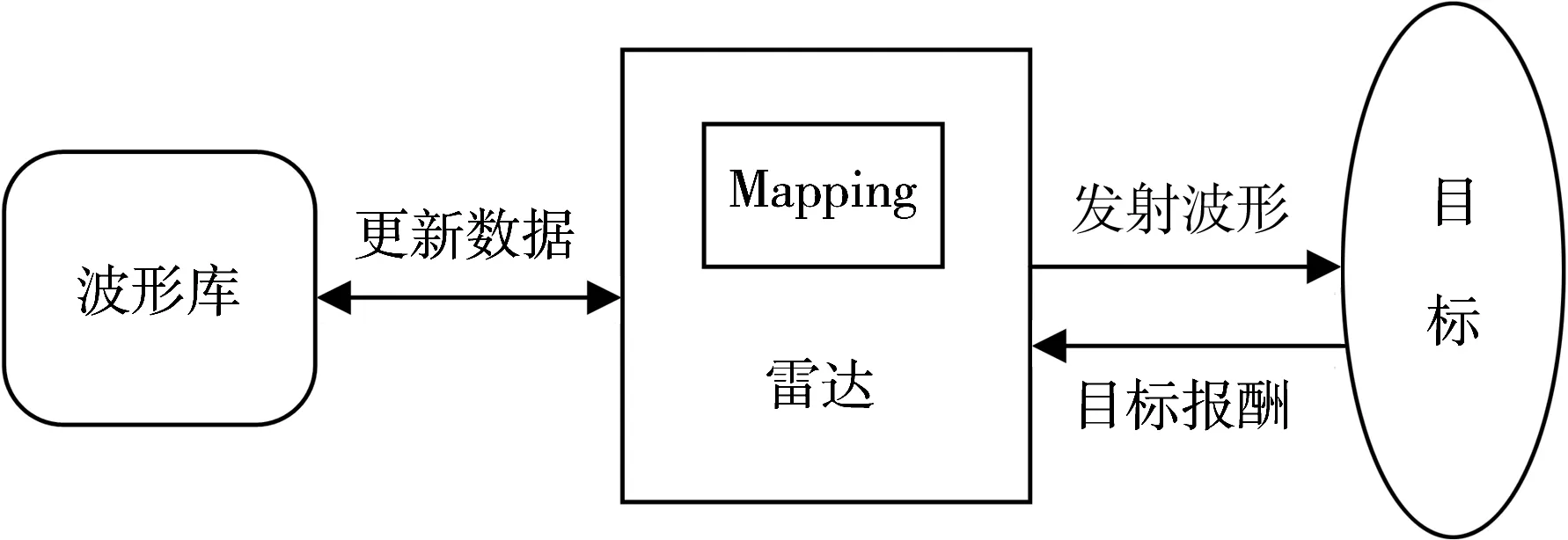
图2 雷达波形选择图示

2.5.1 目标环境空间和雷达波形库的设置

目标环境空间设置为X={1,2,3,…,N}表示环境空间X中有N个不同的目标状态。1,2,3,…,N代表了不同的目标状态,区分出N个目标状态。每一个目标状态都会有一个目标状态变量值pt与之对应。pt为噪声对环境目标的污染值,利用M ATLAB噪声矩阵和随机矩阵产生。

雷达波形库设置为U={1,2,3,…,M},表示雷达波形库U中有M个可供选择的波形。此处1, 2,3,…,M代表了不同的波形,区分出M个波形可供选择。不同的波形对环境的影响不同,最终经过学习将确定出不同环境对应的最优波形。

2.5.2 目标环境报酬函数的设置

由于实际环境的状态情况未知,故只能利用噪声对环境的污染值来估计环境情况[15],令p k为环境变量值,不同的p k代表了不同的环境状态,p k的值由随机噪声对环境的污染值来确定,选取R(p k,u k,p k+1)=p k+1p k-1作为报酬函数。仿真中,利用M ATLAB产生的随机矩阵和噪声函数,对未知环境进行模拟。

2.5.3 建立状态波形映射表(Mapping)

经过雷达对环境的学习认知,目标环境都会对不同的雷达波形产生不同的报酬,从而产生不同的迭代价值。本文把能使迭代价值达到最大的雷达波形与环境状态一一对应起来,此时,2.5.1节中的X和U将组合成一个二维映射表,即每一个状态都将对应于一个最优波形。当雷达进入工作阶段时,雷达将以此表作为选择波形的依据。

2.6 雷达利用改进价值迭代算法进行波形选择的步骤

雷达对波形的选择主要分为两个阶段:学习阶段和工作阶段。学习阶段中,雷达将对未知的环境进行学习和认知,并将认知的结果记录下来。然后,雷达在实际的工作中根据已学习到的波形-状态关系对波形进行选择,以适应不同的目标环境。下面将对这两种环境进行分析。

(1)学习(认知)阶段

步骤1 雷达设置当前状态为x t,并对目标环境随机发生波形,获得当前波形所产生的报酬,并计算出迭代价值V(x t)选取迭代价值最大值所对应的波形作为最优波形u t。

步骤2 雷达根据下一时刻状态再对目标随机发射波形,获得下一状态x t+1的最大迭代价值V(x t+1),并确定最优波形u t+1,并且雷达再根据更新公式更新上一状态x t的迭代价值V(x t+1)。依次往下,每一步都要确定一个新的状态及其对应的波形,同时还要更新上一状态的迭代价值,改变上一状态的最优波形与状态的对应关系。

步骤3 直到迭代达到算法的终止条件,迭代结束。此时,雷达中便形成了一个波形-状态的映射表(Mapping),此表便是以后雷达选择波形的依据。

(2)工作阶段

在此阶段,雷达将根据学习阶段所产生的波形-状态映射表(Mapping)对不同的状态选择不同的波形。如果在此过程中雷达又认知到新的状态,那么它会将新的状态加入到映射表,并更新映射表。

综合以上两个阶段,雷达将工作在一种动态平衡的环境中,即先认知—工作(同时认知)—再认知。这样,雷达便能自适应地对环境作出最优的响应。

3 仿真

本节共进行了2个实验,分别比较了改进型价值迭代算法、策略迭代算法和固定波形选择算法以及常规价值迭代算法的优劣。然后,再对结果加以分析比较,得出结论。

3.1 基本数据设置

由于在实际情况下,这些参数是未知的,需要通过雷达对环境的学习后能得知,实际中的情况该如何选择还需更多的研究。所以在仿真实验中预先设定测量概率、折扣因子和状态转移矩阵的数据来模拟真实环境。其中设定状态空间是4维的,同时使用5种不同的波形对环境进行学习。当目标位于x状态采用u k波形且检测为y时的测量概率如表1所示。折扣因子λ=0.91。

表1 测量概率

由于实际环境的状态情况未知,因此只能利用噪声对环境的污染值来估计环境情况。在MATLAB中,产生随机矩阵和噪声函数对未知环境进行模拟。p k即为k时刻对应的噪声污染值。

选取报酬函数为

实验中将通过对比不同算法的波形选择的准确度来说明各种算法的优劣,现在对波形选择准确度进行如下定义:

波形选择的准确度:在改进价值迭代算法前提下,通过仿真雷达对环境进行认知学习后,将获得一个波形-状态的映射表。将此表与标准的波形选择映射表相对应后,两表将存在一定的差距,即波形选择的误差。将此误差归一化后,得到归一化波形选择误差σ。再用1减去此归一化误差,便得到波形选择的准确度,即波形选择的接近率。

波形选择的准确度(接近率)=1-波形选择的归一化误差率(σ) (20)

3.2 实验一

在实验一中,进行改进型价值迭代算法、策略迭代算法和固定波形选择算法的仿真,通过对波形选择的准确度和测量次数的比较,说明本算法选择波形上的有效性。

分别利用改进型价值迭代算法、策略迭代算法和固定波形选择算法以及设定的数据仿真,得到图3所示的波形选择准确度曲线。

实验一总结:图3中,波形选择的准确度随着测量次数的增加而增加,在相同的测量次数下,可以看出所提改进型价值迭代算法的波形选择准确度要高于固定波形选择算法,但同时要差于策略迭代算法。如果使用策略迭代算法,这种准确度更高。但是,在遇到巨大的测量状态空间和波形空间时,每次策略迭代求解都需要求解等式,要进行大量的计算,此时策略迭代方法的适应能力已经非常差。又因本文提出改进型价值迭代算法的效果已经非常接近策略迭代算法,该算法的优势在于可以不用频繁的求解等式和大量计算的情况下,对波形进行选择,对环境进行判断。那么此时本文所提算法便成为了一种接近最优方案的次优算法,又因其不需要求解等式,免去了繁琐的求解工作,很适用于雷达工作状态。

图3 实验一波形选择的准确度曲线

3.3 实验二

在实验二中,比较改进型价值迭代算法、策略迭代算法与常规价值迭代算法的优劣,通过比较,说明改进型价值迭代算法在波形选择上的优势。

进行改进型价值迭代算法、策略迭代算法与常规价值迭代算法仿真,得到图4所示的波形选择准确度曲线。

图4 实验二波形选择准确度曲线

实验二总结:图4比较了改进型价值迭代算法、策略迭代算法和常规价值迭代算法三种方法。横坐标为波形对环境的测量次数,纵坐标为波形选择的准确度。可以看出,改进型价值迭代算法和常规价值迭代算法的选择准确度都要低于策略迭代算法,同时,常规价值迭代算法还要略优于改进型价值迭代算法。但考虑到策略迭代算法求解等式的繁琐,故改进型价值迭代算法和常规价值迭代算法都有很大的优势,又因为改进型价值迭代算法利用了许多已知的迭代信息,免去了重复计算的计算量,提高了更新速度。所以在雷达探测环境中还是有很大的优势的,再者,从图中可以看出改进型价值迭代算法和常规价值迭代算法已经相差无几。所以,改进型价值迭代算法是一种可行的选择。

4 结束语

自适应波形选择是认知雷达需要解决的核心问题,波形选择的好坏直接影响到认知雷达的工作质量。本文所提出的改进型价值迭代算法,从仿真中可以看到该算法的优点,在相同的测量次数下,改进型价值迭代算法相比固定波形算法有更高的波形选择准确度;相比于常规价值迭代算法而言,虽然波形选择准确度有一定下降但相差无几。关键是在于,改进型价值迭代算法避免了重复计算的计算量,提高了计算速度,提高了雷达工作的效率和自适应能力,这对雷达探测目标环境有着非常积极的作用。所以,综合考虑波形选择准确度和计算量时,改进型价值迭代算法不失为一种良好的可应用于雷达实际环境的自适应算法。未来还需在此基础上进一步研究如何提高改进型价值迭代算法波形选择的准确度,使其自适应能力进一步增强。

[1]LUO Y,ZHANG Q,HONG W,et al.Waveform Design and High-Resolution Imaging of Cognitive Radar Based on Compressive Sensing[J].Science China (Information Sciences),2012,55(11):2590-2603.

[2]GE P,CUI G,KONG L,et al.Cognitive Radar Waveform Design for Coexistence with Overlaid Telecommunication Systems[C]∥IEEE International Conference on Communication Problem-Solving,Beijing:IEEE,2014:5.

[3]WANG B,WANG J,SONG X,et al.Research on Model and Algorithm of Waveform Selection in Cognitive Radar[J].Journal of Networks,2010,5(9): 1041-1046.

[4]WANG B,WANG J,SONG X,et al.Q-Learning-Based Adaptive Waveform Selection in Cognitive Radar[J].International Journal of Communications, Network and System Sciences,2009,2(7):669-674.

[5]GUERCI J R.Cognitive Radar:The Knowledge-Aided Fully Adaptive Approach[M].Boston:Artech House, 2010.

[6]TAO R,LI B,SUN H.Research Progress of the Algebraic and Geometric Signal Processing[J].Defence Technology,2013,9(1):40-47.

[7]NGUYEN N H,DOGANCAY K,DAVIS L M. Adaptive Waveform and Cartesian Estimate Selection for Multistatic Target Tracking[J].Signal Processing,2015,111(1):13-25.

[8]WANG L,WANG H,CHENG Y,et al.Joint Adaptive Waveform and Baseline Range Design for Bistatic Radar[J].Journal of Central South University,2014, 21(6):2262-2272.

[9]XIN F,WANG J,ZHAO Q,et al.Optimal Waveform Selection for Robust Target Tracking[J].Journal of Applied Mathematics,2013,2013(1):1-7.

[10]叶映宇,文铁牛,陈俊,等.外辐射源雷达运动目标信号特性及检测方法研究[J].雷达科学与技术,2014, 12(6):604-608,612.

[11]MCDILL K K,MINCHEW C D.Waveform Selection for an Electrically Enhanced Seine for Use in Harvesting Channel Catfish Ictalurus Punctatus from Ponds[J].Journal of the World Aquaculture Society, 2001,32(3):342-347.

[12]WONG T F,LOK T M,LEHNERT J S.Asynchronous Multiple-Access Interference Suppression and Chip Waveform Selection with Aperiodic Random Sequences[J].IEEE Trans on Communications,1999,47(1):103-114.

[13]KOJIMA H,OMURA Y,MATSUMOTO H,et al.Automatic Waveform Selection Method for Electrostatic Solitary Waves[J].Earth,Planets and Space,2000,52(7):495-502.

[14]ZHAO Y,FENG J,ZHANG B,et al.Current Progress in Sparse Signal Processing Applied to Radar Imaging[J].Science China(Technological Sciences), 2013,56(12):3049-3054.

[15]李静.基于自适应动态规划的波形选择方法研究[D].沈阳:东北大学,2009.