基于多目标遗传优化算法的PSA贴敷机单驱形式横梁研究
2015-01-21王西峰康运江苗振海
魏 淼,王西峰,康运江,苗振海
(1.机械科学研究总院,北京 100044;2.机科发展科技股份有限公司,北京 100044)
0 引言
PSA 贴敷机能够实现PSA 自动化贴敷,通过模组实现XY 向精确定位。现采用龙门双驱结构,但由于横梁双电机驱动造成的同步性控制问题难以解决,设备不能有效提高生产效率。本文通过采用单驱结构来避免同步性控制,完成横梁参数化设计。
设备定位系统结构中,横梁作为主要移动部件,其机械精度是影响设备贴装精度的重要因素之一。本文通过Pro/E 和Workbench 协同仿真完成单驱横梁的参数化设计,并保证机械精度在±0.04mm 范围之内。
1 建立数学参数模型
横梁参数模型涉及尺寸优化,尺寸优化关键步骤是确定目标函数和设计变量。横梁结构及参数定义如图1所示。其中,Width 表示横梁截面宽度,Hight 表示截面高度,N 表示横梁掏空孔个数,Nlength 表示掏空孔截面长度,壁厚均设置为20mm。
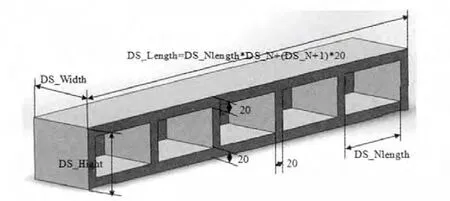
图1 模型参数定义Fig.1 The parameter definition of model
确定设计变量参数为:
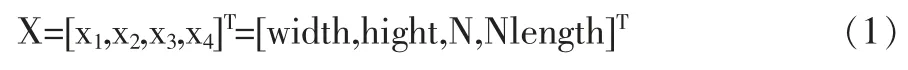
式(1)中变量N 无量纲,其余单位为mm。PSA 贴敷机对横梁有尺寸设计要求,因此可以定义变量X 在数学模型中的约束条件。在式 (2) 中,初始变量值为X0=[160,140,5,120]T,上下限值U=[180,160,8,200]T、L=[140,120,3,80]T。
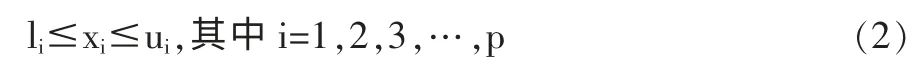
横梁参数化模型的目标函数如式(3)~(5),其中s(Xi)表示横梁运行过程中的变形量,f一阶(Xi)表示横梁的一阶模态固有频率,m(Xi)表示横梁质量。

综上所述,横梁参数化设计的数学模型为:
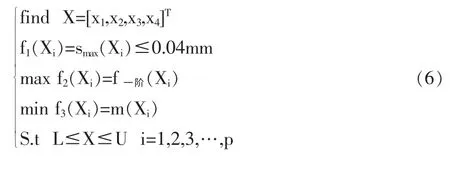
2 横梁参数优化设计
2.1 横梁参数化建模
通过Pro/E 建立横梁的参数化模型,将模型导入Workbench 中分析。在Workbench 中引入模态分析模块和瞬态动力学分析模块,然后进行Pro/E 和Workbench协同仿真。
2.2 多目标遗传算法优化
各参数设定好之后对横梁进行优化。优化过程包括实验设计、响应面和优化三部分。首先通过蒙特卡罗抽样技术采集实验样点,计算每个实验样点的响应结果,然后通过二次插值构造出设计空间响应曲面,最后基于响应曲面完成目标函数的参数优化,选出满足要求的解集。
实验设计采用中心复合设计法,Workbench 根据数学模型中设计变量的上下限矩阵自动生成了25 个实验样点,根据这25 个实验样点值计算出响应结果,并生成响应曲面,得出拟合度和灵敏度等结果,方便数据处理。
2.3 横梁优化结果分析
(1)拟合度曲线。根据响应面结果生成拟合度曲线,曲线上的点表示输出参数预估值与实验样点观察值的比值,用来判定响应面是否拟合实验样点。如图2 所示,图表横坐标为设计点观察值,纵坐标为响应面预测值,图中的实验样点基本接近对角线,该实验中得到的响应面拟合度较好。
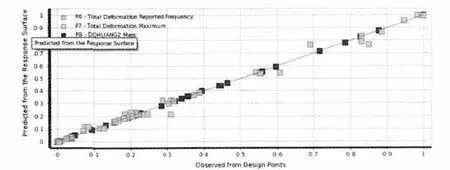
图2 目标函数的拟合度Fig.2 Goodness of fit of the objective function
(2)响应面。Workbench 可以根据响应面结果生成二维或三维响应曲面。通过响应曲面查看各输入参数对输出参数的影响,选择判断合适参数。
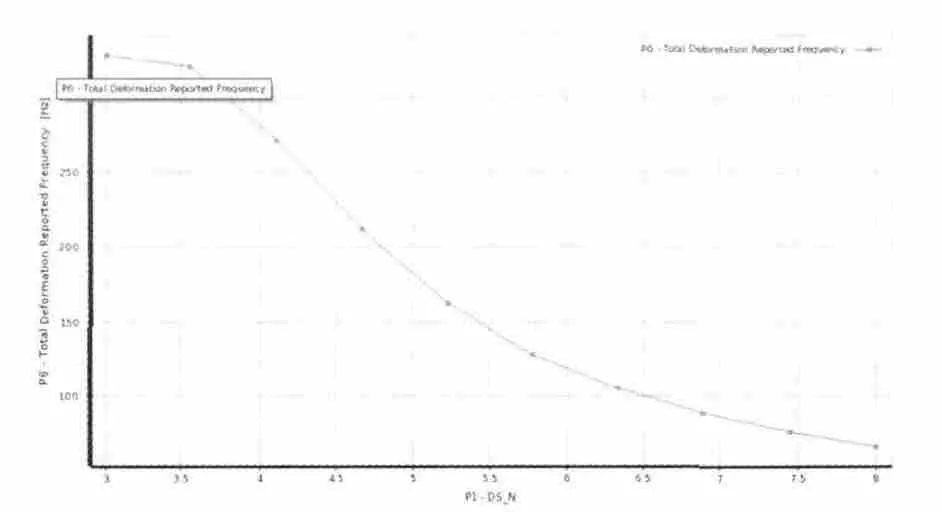
图3 一阶模态固有频率对输入参数N 的响应曲线Fig.3 The response curve of the one modal natural frequency to N
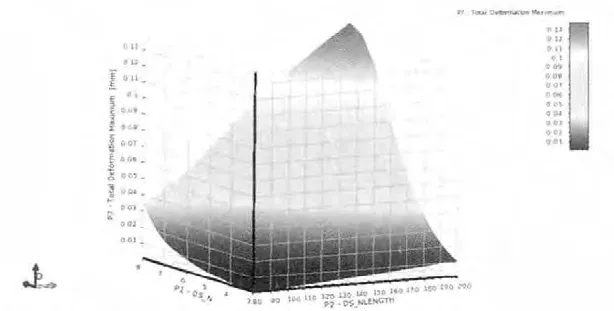
图4 横梁最大变形量对输入参数N 和Nlength 的响应曲线Fig.4 The response curve of the beams maximum deformation to N and Nlength
若观察单独输入变量对输出变量值的影响,采用2D云图,如图3 为输入参数N 对一阶模态固有频率影响,一阶固有频率负相关于参数N。若观察两个输入变量对一个输出变量的影响,采用3D 云图,图4 为输入参数N 和Nlength 对横梁最大变形量影响,横梁最大变形量正相关于N 和Nlength。设备要求横梁最大变形量在±0.04mm 范围内,因此,最优解选择最大变形量在0.04mm 值以下。
(3)局部灵敏度。局部灵敏度分析连续输入参数对输出参数的影响,是基于单个输入参数变化下输出参数的变化。本文截取灵敏度条状图结果,条状图分成三个纵栏,分别表示三个不同的输出参数,每一栏中不同颜色的条框代表不同的输入参数。条状图中灵敏度有大小和正负两种含义,其中大小表示输入参数在输出参数所占的权重;正负则表示该输出参数与输入参数呈正 (负)相关关系。各参数对目标函数的灵敏度条状如图5 所示。
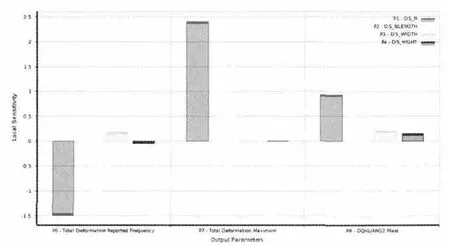
图5 目标函数的局部灵敏度Fig.5 Local Sensitivity of the objective function
由灵敏度图可以看出,参数N 和Nlength 对横梁一阶模态固有频率影响权重最大,且呈负相关性;对横梁运行过程中最大变量值影响最大,且呈正相关性;对横梁质量影响较大,呈正相关性。还可以发现,横梁截面尺寸对横梁的最大变形量几乎没有影响,对横梁的质量有影响。
3 横梁参数化优化结果
完成上述结果分析之后,通过Workbench 生成各参数图表并找出最优解。按优先级比较,各组解首先要保证横梁的最大变形量在±0.04mm 范围之内,其次保证横梁质量尽量小,最后要求横梁一阶模态固有频率满足避免共振的要求。
3.1 横梁参数化计算结果
根据实际情况输入参数N 是整数,故优化数据结果分成6 组。根据局部灵敏度的分析,输出参数横梁质量与横梁截面的长宽呈正比关系,故在结果提取过程中保证横梁截面尺寸在上下限范围之内越小越好。在参数化分析计算结果中,得到表1 数据。
表中N 为整数,无量纲,Nlength、Width、Hight、Length四个输入参数单位均为mm,f1 表示在横梁实际运行中的最大变形量,f2 表示横梁的一阶模态固有频率,f3 表示横梁质量。
对上述表格数据进行分析: 将横梁截面尺寸设置在允许范围内最小值,根据灵敏度分析,f1 与参数Nlength 呈正相关关系。当输入参数N 为7 和8 时,输入参数Nlength 为最小值时,横梁最大变形量f1 最小为0.048mm 和0.58mm,超过设计允许范围之内。当N 分别为3、4、5、6 时,均可以满足设计条件。
当N 为6 时,Nlength 的最大值为166mm,此时横梁的最大加速度值为一个g 值。当N 小于6 时,横梁输入参数Nlength 和输出参数最大变形量均有提升的空间,同时横梁的最大加速度值也可以提升,这样便能有效地提高设备定位系统的工作效率。
3.2 横梁改动前后对比
根据现有PSA 贴敷设备双驱动形式结构梁尺寸数据,选取参数为优化之后的横梁参数。令横梁结构尺寸: Width=140mm、Hight=120mm、N=4、Nlength=182mm。计算得到横梁长度: Length=828mm,跨距688mm,原双驱动横梁长度826mm,跨距690mm。
用优化后的设计变量重新生成模型,并与原来模型进行对比分析如表2 所示。表中定义Vmax为横梁所能达到的最大速度,定义amax为横梁在运行过程中达到的最大加速度值,根据数据分析得出结论: ①当速度为1m/s和1.75m/s,加速度为10m/s2和17.5m/s2时,优化前的结构均不满足机械精度要求,优化后的横梁均能达到要求;②当速度为1m/s,加速度为10m/s2时,优化后的模型相对于优化前最大变形量降低62.7%,当数值为1.75m/s 和17.5m/s2时,优化后的模型相对于优化前最大变形量降低63.9%;③优化后的横梁相对于优化前的横梁一阶模态固有频率提高75%。
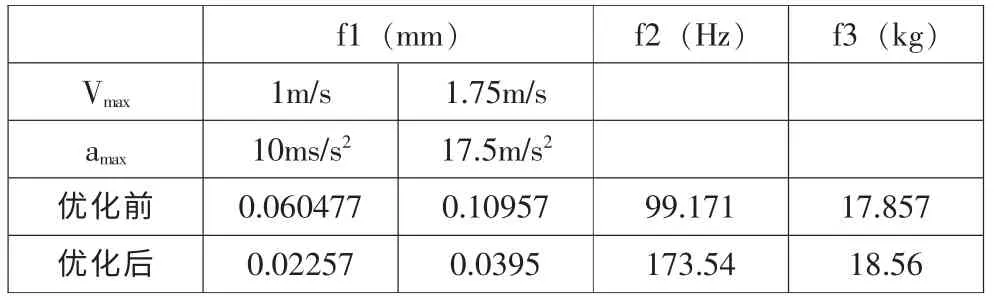
表2 模型优化前后各目标函数值对比Tab.2 The comparison of the objective function value before and after the model optimization
4 结论
(1)本文建立了横梁的参数数学模型,并根据数学模型建立了横梁的参数化模型。
(2)通过Pro/E 与Ansys Workbench 的协同仿真,基于模态分析和瞬态动力学分析对横梁进行了参数优化设计,得出了满足设计要求的最优解。
(3)得出最优解横梁参数,生成横梁模型进行模态分析和瞬态动力学分析,优化后的模型相对于原有模型的一阶固有频率提高75%,横梁最大变形量在某一工况条件下提高62.7%。
[1] 张翔,陈建能.机械优化设计[M].北京:科学出版社,2012.
[2] 黄志新,刘成柱.ANSYS Workbench 14.0 超级学习手册[M].人民邮电出版社,2013.
[3] 陈伦军.机械优化设计遗传算法[M].北京,机械工业出版社,2005.
[4] 王艳.旋挖钻机回转平台的结构分析及优化设计[D].长安大学硕士学位论文,2013.
[5] 韩静,方亮,等.基于Pro/e 与ANSYS WORKBENCH 仿真及优化的复杂装配件协同[J].机械设计与制造,2010,1.
[6] 卫军胡(译).蒙特卡洛方法在系统工程中的应用[M].西安:西安交通大学出版社,2007.
