例谈数学练习的变式设计

孙开飞

好奇心是小学生重要的心理特征之一，心理学研究表明：儿童最初的求知欲都是由好奇心发展而来的，且伴随着知识、能力的增长，他们的好奇心会进一步得到满足，愉快的情感体验才能增强。大凡优秀的数学老师，总能设计出具有奇异感的练习题，从而产生“奇”效。那么，如何才能设计出具有奇异感的练习题呢？

一、 设计迷惑性练习

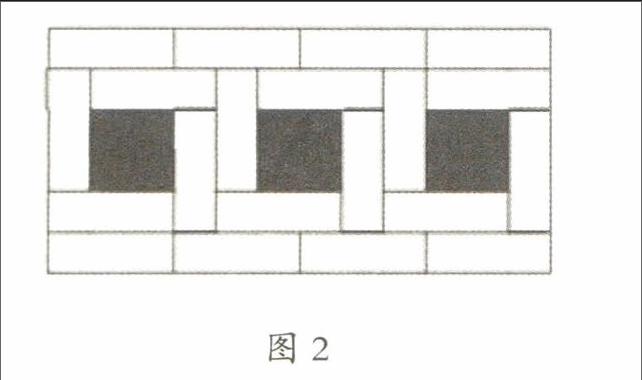
迷惑性练习就是掩盖知识的本质特征，给学生造成迷惑与假象，使其在探索与交流中，发现知识的本质，从而激发学生的求知欲望。例如在“圆的周长”练习课中，一位教师设计了这样一道具有迷惑性的练习：如图1，在一个圆的直径上画三个小圆，有两只蚂蚁以相同的速度，甲绕外面的大圆爬一圈，乙绕里面的每个小圆爬一圈，想一想谁先回到起点？

这样的练习一出现，就引起了学生的争论：有学生认为乙先到，因为走内部近些，生活中的“抄近路”就是走中间的路近；有些学生认为甲先到，因为走外面只是一个大圈，而内部要转许多的弯；也有学生认为可能一样，因为速度相等，关键看所行的路程怎样。这样的结论都是学生凭直觉做出的判断，接着教师引导学生验证自己的猜想：又该怎样说明结论正确与否呢？最后再次拓展：如果中间再有更多这样的小圆，他们周长相等吗？

在这样的练习过程中，通过迷惑性练习的假象，给学生直观的错误“提示”，进而引导学生观察——猜想——验证，在一系列的数学思维活动中，对知识的本质特征，有了较为清楚的认识，达到有效训练的目的。

二、 设计诱发性练习

小学生在学习新知时，容易将新知识与一些形似神异的旧知识相混淆。这就需要教师在知识的易混处，巧设陷阱，将学生学习过程中的疑难问题和错误认识诱发出来，进而引导学生质疑、释疑，触及知识的本质属性，从而及时纠正错误。如学习“正反比例的判断”时，学生往往不能很好地运用意义进行判断，易受一些形似神非的题目所迷惑，教师可以将以下的一些易错题型一一出示，引导学生比较，思考其正确性：

1.圆的周长和半径成正比例。（误认为缺少定值而判错）

2.圆的面积和半径成正比例。（受上题的影响误判对）

3.三角形的面积和底成正比例。（缺少定量误判对）

4.正方体的高一定，体积和底面积成正比例。（是恒等式，学生误判为对）

……

通过题组训练的方法，可以增强学生在解题时的“免疫力”，将可能出现的错误防患于未然。

三、 设计隐蔽性练习

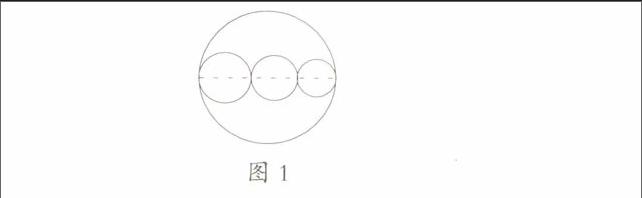
大量机械重复的训练，不但容易使学生疲劳，也会使学生的思维产生消极定势，因而我们可以将问题的数量关系，用隐蔽的方式加以呈现，调动学生思维的积极性，进而培养学生追根问底、努力探索的热情。例如在学完“比”的知识后，笔者设计了这样的一道题：如图2，用同样大小的长为6厘米的长方形围成大长方形，（1）求图中大小长方形长与宽的比。（2）求图中阴影部分的面积。

学生刚接触此题时，纷纷认为缺少条件，但我明确地告诉他们，本题条件充分，关键在于找出关系。于是学生都被这道只有一个条件的怪题所吸引，不自觉地投入到探索隐蔽条件的活动中去。通过仔细观察图形后得出结论：对于小长方形而言，4条小长方形的长=3条小长方形的长+3条小长方形的宽，所以1条小长方形的长=3条小长方形的宽，所以小长方形长与宽的比是3∶1。有了这个条件后，其他问题就迎刃而解了。

当然，设计隐蔽性练习，是为了激发学生探究的热情，促使学生善于观察、勤于思考，但也不能一味地追求难度而超出学生的认知范围，同时这样的题型不宜过多，应适可而止，否则会使一些学有困难的学生感到数学太难，从而产生畏难情绪。

四、 设计蕴含性练习

《数学课程标准（2011版）》将基本数学思想列为“四基”目标之一，这就要求教师能从外现的数学知识中，理解并发掘数学练习中所蕴含的数学思想，从而拓展学生对数学的认识。

例如“转化”思想是一种重要的数学思想，小学阶段许多数学新知识就是将其转化成学生已学的旧知识，从而实现知识结构的拓展与同化。那么学生对这样的数学思想到底有怎样的认识呢？笔者曾做了这样的一次练习。

（2）要使等式4○7+○63+15○=1000成立，则每个○中应各填什么数字？

这样的练习，既有知识与思想蕴含其中，也凸现了学生的自学能力与探索过程，实现了“方法与过程”的统一。

当然，数学练习出“奇”制胜的方法还有很多，关键在于教师对平常的习题多留心、多思考，从寻常的练习中发现、创造出不寻常的亮点，调动学生多种感官的参与，激发其学习兴趣，从而获得事半功倍的效果。

【责任编辑：陈国庆】