First Principles Study of Uranium Solubility in Gd2Zr2O7Pyrochlore

Qing-yun Chen,Ki-min Shih,Chun-min Meng,Lie-lin Wng,Hu Xie,To Wu

a.Key Subject Laboratory of National Defense for Radioactive Waste and Environmental Security, Southwest University of Science and Technology,Mianyang 621010,China

b.Department of Civil Engineering,The University of Hong Kong,Pokfulam Road,Hong Kong SAR, China

c.Key Lab for Shock Wave and Detonation Physics Research,Institute of Fluid Physics,Chinese Academy of Engineering Physics,Mianyang 621900

(Dated:Received on June 8,2015;Accepted on August 1,2015)

First Principles Study of Uranium Solubility in Gd2Zr2O7Pyrochlore

Qing-yun Chena,Kai-min Shihb∗,Chuan-min Mengc∗,Lie-lin Wanga,Hua Xiea,Tao Wua

a.Key Subject Laboratory of National Defense for Radioactive Waste and Environmental Security, Southwest University of Science and Technology,Mianyang 621010,China

b.Department of Civil Engineering,The University of Hong Kong,Pokfulam Road,Hong Kong SAR, China

c.Key Lab for Shock Wave and Detonation Physics Research,Institute of Fluid Physics,Chinese Academy of Engineering Physics,Mianyang 621900

(Dated:Received on June 8,2015;Accepted on August 1,2015)

Ab initio calculation is performed to investigate the uranium solubility in different sites of Gd2Zr2O7pyrochlore.The Gd2Zr2O7maintains its pyrochlore structure at low uranium dopant levels,and the lattice constants of Gd2(Zr2−yUy)O7and(Gd2−yUy)Zr2O7are generally expressed as being linearly related to the uranium content y.Uranium is found to be a preferable substitute for the B-site gadolinium atoms in cation-disordered Gd2Zr2O7(where gadolinium and zirconium atoms are swapped)over the A-site gadolinium atoms in ordered Gd2Zr2O7due to the lower total energy of(Gd2−yZry)(Zr2−yUy)O7.

Gd2Zr2O7pyrochlore,Nuclear waste,Uranium solubility,Density functional theory

I.INTRODUCTION

The emergence of nuclear energy offers promising opportunities for the development of inexpensive and highly efficient energy sources.However,the safe disposalof large amounts ofnuclear waste,especially longlived radioactive elements,remains an important challenge for the nuclear industry[1,2].Gadolinium zirconate(Gd2Zr2O7)pyrochlore exhibits high chemical durability,radiation resistance,and solubility for large radionuclide species(such as thorium,uranium,and plutonium)and is therefore an attractive candidate as a nuclear-waste host material[3−9].

In an ordered A2B2O7pyrochlore structure(space group Fd3m)with A(gadolinium or rare earths)and B(zirconium,titanium,tin,hafnium,or plumbum) cations ordered on the 16d(0.5,0.5,0.5)and 16c(0, 0,0)sites,respectively,oxygen can be found at the 48f (x,0.125,0.125)and 8b(0.375,0.375,0.375)positions. The 8a(0.125,0.125,0.125)site is vacant(using the Wyckoff notation)[10,11].Gd2Zr2O7crystallizes in the cubic pyrochlore structure,and large quantities of act inide elements are expected to be incorporated into the matrix at both the gadolinium and zirconium lattice positions[12−15].

Sickafus et al.[6]concluded that the use of radiationtolerant materials in the 2:2:7 pyrochlore stoichiometry phase presented no advantage.The key to radiation tolerance is an inherent ability to accommodate atomic lattice disorder.Under ion irradiation,the ordered pyrochlore superstructure is transformed into an anion-disordered pyrochlore before its final transformation into a cation-disordered defect-fluorite structure type[16].It has been shown that Gd2Zr2O7is transformed into a radiation-resistant anion-deficient fluorite structure upon irradiation and shows greater radiation resistance than Gd2Ti2O7,which has greater defect formation energy disorder and is more susceptible to amorphization[3].Regarding the primacy of cation or anion disorders,inconsistent conclusions can be obtained.For example,diffraction studies indicated that oxygen disorder caused cation disorder,while spectroscopy studies yielded the opposite conclusion[11].Although the underlying mechanisms of defect formation and radiation resistance are not yet wellunderstood,there is a consensus that the accommodation of lattice disorder should improve amorphization resistance in a displacive radiation damage environment[3,6,10].

Kulkarni et al.[17]reported that plutonium can completely replace gadolinium(A site)in a Gd2Zr2O7matrix.However,uranium can replace only 40%of the gadolinium at the A site in the Gd2Zr2O7matrix, while it can replace all of the zirconium at the B site. The structure of Gd2Zr2O7is transformed from a pyrochlore into a closely related fluorite structure as the level of uranium dopant increases[12].By controlling the sintering atmosphere,uranium with various oxidation states and ionic radii can be incorporated into a Gd2Zr2O7matrix along with pyrochlore and defect fluorite structures[18].

Gregg et al.[19]recently examined U-doped and off-stoichiometric Gd2Zr2O7pyrochlore via X-ray diffraction(XRD)and X-ray absorption near-edge structure (XANES)spectroscopy.They suggested that uranium cations are largely located at pyrochlore B sites instead of the targeted A sites.The study provided direct evidence for cation antisite disorder in U-doped Gd2Zr2O7pyrochlore[19].Although some experimental studies have considered a solution of high-level radioactivewaste uranium in Gd2Zr2O7pyrochlores,the mechanisms that underlie uranium doping and disorder(defect formation)in Gd2Zr2O7crystals are not yet well understood.

First principles density functional theory(DFT)simulations have become ideal tools for the systematic investigation of properties other than chemical compositions.In this work,the virtual crystal approximation(VCA)method is used to calculate the total energies and structure properties of U-doped Gd2Zr2O7pyrochlores(ordered and cation-disordered structures). The solution behavior of uranium in Gd2Zr2O7pyrochlores is also clarified.

II.COMPUTATIONAL METHOD

The calculations are performed using the firstprinciples plane-wave pseudopotential method based on DFT incorporated into the CASTEP computational code[20].The exchange-correlation energy of the electrons is described according to the local-density approximation(LDA)framework[21].The Coulomb potential energy caused by electron-ion interaction is described with the ultrasoft scheme,in which the orbits of Gd(4f7,5s2,5p6,5d1,6s2),Zr(4s2,4p6,4d2,5s2), U(5f3,6s2,6p6,6d1,7s2),and O(2s2,2p4)are treated as valence electrons.The electronic wave functions are expanded in a plane wave basis set with an energy cutoff of 500 eV.A Monkhorst-Pack mesh with 3×3×3 k-points is used for Brillouin-zone k-point sampling, and the self-consistent convergence of total energy is 2×10−6eV/atom.These parameters are sufficient to achieve well-converged total energy and geometric configurations.

The VCA method is used to model four series of configurations,including(Gd2−yUy)Zr2O7, Gd2(Zr2−yUy)O7,(Gd2−yZry)(Zr2−yGdy)O7,and (Gd2−yZry)(Zr2−yUy)O7,to study the solution behavior of uranium at various sites on a Gd2Zr2O7lattice. The VCA in CASTEP is capable of correct describing a number of mixture atoms[22].The VCA method performed well even when applied to elements that were far apart on the periodic table[23−26].The atomic sites in a disordered crystal can be described in terms of a hybrid atom that consists of two element types.The relative concentrations can be set for any number of atoms,and the total concentration must be 100%.Using the VCA method,the uranium atoms can be distributed randomly in the Gd2Zr2O7lattice,and any percentage of uranium content can be introduced to the disordered system.

The full structural relaxations for all of the configurations are performed first.During structure optimization,the totalenergy is minimized by varying the lattice constants according to the restrictions ofthe given symmetry.The crystaland electronic structures ofallseries are then calculated.Because structural phase changes from pyrochlore to fluorite are observed at higher y values[12],y=0 to 0.4 for all series in this study.The VCA method is adopted,according to which the uranium atoms that occupy the lattice site are described via the index y(i.e.,the atomic fraction of uranium at the lattice site)to model the solubility of the uranium in the Gd2Zr2O7pyrochlore.The calculation results are given as statistical average values.

III.RESULTS AND DISCUSSION

Table I presents the lattice constants,internal positional parameter xO48f,and bond distances between the nearest-neighboring cations and anions of the Gd2Zr2O7pyrochlore.The calculated lattice constants a and xO48fare 10.37˚A and 0.340,respectively,and are therefore in agreement with the experimental[4, 18]and other calculated[10,28,29]results.The bond distances between the nearest-neighboring cations and anions are also in agreement with other results[4].The tight-binding(TB)[10]and DFT with energy correction(DFT+U)approaches[28]exhibit greater lattice constants and bond lengths of Gd2Zr2O7pyrochlore. Although the TB approach is based on quantum mechanics,it lacks reliability and transferability due to the parameterization of the electronic Hamiltonian with a finite set of equilibrium structures and properties,and even lacks self-consistency in most cases.

The cubic lattice constant and positional parameter of xO48fcan be used to completely describe the pyrochlore structure.Figure 1(a)exhibits the calculated lattice constants a as a function of the uranium content y in(Gd2−yUy)Zr2O7and Gd2(Zr2−yUy)O7to clarify the fundamental properties of U-doped gadolinium zirconate pyrochlore.Vegard’s law is valid below y=0.3,and the lattice constants of Gd2(Zr2−yUy)O7and(Gd2−yUy)Zr2O7are generally expressed as possessing a linear relationship to the uranium content y.Although the lattice constants of Gd2(Zr2−yUy)O7increase with the enriched uranium content,the (Gd2−yUy)Zr2O7series shows the opposite tendency.

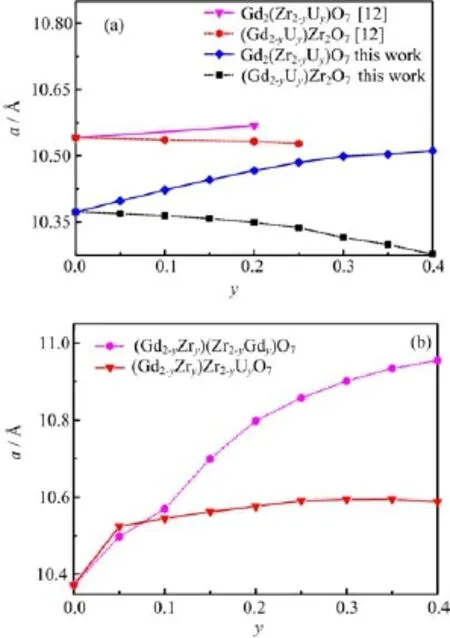
FIG.1 The calculated lattice constants a as a function of y in(Gd2−yUy)Zr2O7,Gd2(Zr2−yUy)O7,and (Gd2−yZry)(Zr2−yUy)O7and cation disorder parameter y in(Gd2−yZry)(Zr2−yGdy)O7.(a)Lattice constants a of(Gd2−yUy)Zr2O7and Gd2(Zr2−yUy)O7compared with those results in Ref.[12],and(b)lattice constants a of (Gd2−yZry)(Zr2−yUy)O7and(Gd2−yZry)(Zr2−yGdy)O7.

TABLE I The lattice constants,internal positional parameters xO48f,and bond distances between the nearest-neighboring cations and anions of the Gd2Zr2O7pyrochlore.

It has been observed that the increase in the lattice constant of(Gd2−yUy)Zr2O7is related to the difference in the ionic radii of the gadolinium and uranium ions and that the decrease of Gd2(Zr2−yUy)O7is related to the incorporation of the larger uranium ion at the zirconium site[12].The differences between the calculated lattice parameter and the available experimental results are all within 1.7%,which indicates that the calculation results of the current study are fairly trustworthy.The lattice expansion is obviously expressed along with the degree of cation disorder,as shown in Fig.1(b).Previous studies have also expressed linear lattice constants related to the indium composition x in InxAl1−xN and to the cation disorder index x in (Mg1−xAlx)[MgxAl2−x]O4[30,31].

The lattice constants present obvious variations when y＞0.4(data not shown).The variation mainly involves the loss of pyrochlore ordering above this concentration level[12].Therefore,the pyrochlore structure model for high uranium content is not suitable.The results of y＜0.2 are considered in the following discussion.

Figure 2 shows the variations in the optimized bond length as a function of the uranium content y or cation disorder parameter y.Although the bond length between O and its nearest-neighboring cations gradually increases with increasing uranium content in Gd2(Zr2−yUy)O7,the opposite holds true for(Gd2−yUy)Zr2O7.No obvious changes in the bond length between the O-and B-site cations are observed. The bond lengths dA−O8band dB−48fobviously increase along with the increasing cation disorder parameter y in(Gd2−yZry)(Zr2−yUy)O7.The change in the tendency of the lattice parameters(see Fig.1)is similar to the change in the tendency of dA−O8b(the bond length between the A-site cation and O8b)and dB−O48f(the bond length between the B-site cation and O48f),exhibiting a certain regularity and a preferable relativity. The lattice constant of the pyrochlore is determined by dA−O48fand dB−O48f,which are short bond lengths that exhibit strong interactions between the related atoms.

The electron density difference is typically the difference between an assumed standard or model electron density and the actual observed or DFT-computed electron density.The difference provides information related to electron transfer and distribution after bonding.The electron density differences of Gd2Zr2O7,Gd2(Zr2−yUy)O7, (Gd2−yUy)Zr2O7,(Gd2−yZry)(Zr2−yGdy)O7,and (Gd2−yZry)(Zr2−yUy)O7are shown in Fig.3,in which the bright(red)and darker(blue)areas indicate positive and negative electron transfer,respectively.

In general,a covalent interaction exists between the B-site cations and the nearest-neighboring O, and an ionic interaction exists between the A-site cations and the nearest-neighboring O.No obvious electronegativity changes are seen in(Gd2−yUy)Zr2O7and Gd2(Zr2−yUy)O7.The changes in the lattice constants of(Gd2−yUy)Zr2O7and Gd2(Zr2−yUy)O7are related to the difference in the change in the ionic radii after doping.Furthermore,the latticeconstant changes of(Gd2−yZry)(Zr2−yGdy)O7and (Gd2−yZry)(Zr2−yUy)O7are related to the electronegativity change of the cation sites that arise from atom swapping or doping.

FIG.2 The variations in the optimized bond length as a function of y in(Gd2−yUy)Zr2O7,Gd2(Zr2−yUy)O7and (Gd2−yZry)(Zr2−yUy)O7and cation disorder parameter y in(Gd2−yZry)(Zr2−yGdy)O7.(a)dA−O8b,(b)dA−48f,and (c)dB−48f.

FIG.3 Electron density difference of(a)Gd2Zr2O7,(b)Gd2(Zr2−yUy)O7,(c)(Gd2−yUy)Zr2O7,(d) (Gd2−yZry)(Zr2−yGdy)O7,and(e)(Gd2−yZry)(Zr2−yUy)O7.

A high level of Coulomb repulsion exists between two atoms with high electronegativity.As shown in Fig.3(d),the A-site electronegativity in the(Gd2−yZry)(Zr2−yGdy)Olattice obviously increases (i.e.,more red areas)due to cation disorder.The Coulomb repulsion between the A-site atoms and O8bincreases,and the ionic bond dA−O8bincreases while the Coulomb repulsions are dominant.The covalent bond plays a dominant role in the bond dB−O48f,which increases due to the introduction of atoms with larger ionic radii in the B sites.

The lattice constant of pyrochlore is determined by the short bond lengths dA−O8band dB−O48f.Therefore,the lattice parameter of(Gd2−yZry)(Zr2−yGdy)O7obviously increases with the increase in cation disorder,and the(Gd2−yZry)(Zr2−yUy)O7case has fewer lattice parameter increases due to the less increase in electronegativity in the B-site atoms.

The total energy of(Gd2−yUy)Zr2O7and (Gd2−yZry)(Zr2−yUy)O7gradually increases with the uranium content y(see Fig.4).With the increase of cation disorder y,the total energy of (Gd2−yZry)(Zr2−yGdy)O7increases linearly,which suggests the instability of the higher cation disorder.This finding is comparable with the total energy difference between(Gd2−yUy)Zr2O7and (Gd2−yZry)(Zr2−yUy)O7of the same uranium content y,as the two structures have the same numbers and kinds of atoms.(Gd2−yZry)(Zr2−yUy)O7structures have lower total energy and are more stable than (Gd2−yUy)Zr2O7structures when the y values are the same.

Studies using synchrotron XRD,XANES,and positron annihilation lifetime spectroscopy have suggested that the uranium cation in doped gadolinium zirconates(Gd2−xUxZr2O7,x=0.1 and 0.2)is largely located at the pyrochlore B site instead of at the targeted A site[19].Based on the total energy calculation, uranium is a more preferable substitute for the B-site gadolinium atoms in cation-disordered Gd2Zr2O7than for the A-site gadolinium atoms in ordered Gd2Zr2O7due to the former’s lower total energy.Finally,there is little total energy variation in(Gd2−yZry)(Zr2−yUy)O7due to the small differences in the atomic energy andionic radius between zirconium and uranium[32].

FIG.4 Total energy as a function of y(uranium content and cation disorder parameter).

FIG.5 The O48fpositional parameter x(xO48f)as a function of y(uranium content and cation disorder parameter).

All of the atoms in an ideal pyrochlore,with the exception of 48f(O48f),are located at special positions. Thus,the structure is completely described by the lattice parameter a and the fractionalcoordinate x of O48f[33].The O48fpositional parameter x(xO48f)is an important indicator of a pyrochlore’s degree of disorder and resistance to irradiation-induced amorphization[34].As shown in Fig.5,the xO48fvalues of a U-doped pyrochlore do not obviously change with an increase in the uranium content.This finding suggests that the gadolinium zirconate pyrochlore is a good uranium immobilization matrix that can maintain its radiation tolerance in the case of low uranium content doping.The xO48fvalues of the cation disorder series(Gd2−yZry)(Zr2−yUy)O7obviously increase when y＞0.1.

Lian et al.observed that the radiation resistance of pyrochlore was closely related to the cation ionic radius ratio and x positional parameter xO48f[35].A decrease in the average ionic radius ratio of the A and B sites(rA/rB)generally leads to a decrease in the critical temperature for amorphization and a resistance to radiation damage.Furthermore,the radiation resistance of Gd2(Ti1−xZrx)2O7increases as the concentration of zirconium increases[36].The high radiation resistance of Gd2Zr2O7is caused not only by the high neutron absorption cross-section of gadolinium,but also by the transformation of the pyrochlore structure into a defectfluorite structure,with the disordering ofcation antisite defects(A and B cations that exchange places)coupled with the disordering of oxygen Frenkel pairs(a 48f oxygen is moved to an adjacent empty 8a site,resulting in a vacant 48f oxygen site and an occupied 8a oxygen site).

Gregg et al.[19]suggested that cation disordering is important to increase ionic conductivity and increase resistance to radiation-induced amorphization in pyrochlores.Pyrochlores have the general formula A2B2O7,in which A is usually occupied by the larger cation and B is occupied by the smaller cation.The stability of the pyrochlore structure is governed by the ionic radii ratio of the A to B cations(rA/rB)[10], which is affected by the disorder,the ionic value,and the substitution site of the doping atom.The high radiation resistance of the Gd2Zr2O7pyrochlore can be attributed to the similar ion radii of the A-and B-site atoms,which easily change into highly radiationresistant fluorite structures[3].It has been consistently concluded that the radiiratio ofthe A to B sites(rA/rB) decreases as y increases in(Gd2−yZry)(Zr2−yGdy)O7. Furthermore,the positional parameter xO48fincreases and shows greater radiation resistance capability.

IV.CONCLUSION

In this work,the VCA method is used to calculate the total energy and structural properties of U-doped Gd2Zr2O7pyrochlores(i.e.,both ordered and cation-disordered structures).The Gd2Zr2O7maintains its pyrochlore structure at low uranium dopant levels,and the lattice constants of Gd2(Zr2−yUy)O7and(Gd2−yUy)Zr2O7are generally expressed as a linear Vegard’s relationship to the uranium content y.As the uranium content is enriched,the lattice constants of Gd2(Zr2−yUy)O7increase.However,the(Gd2−yUy) Zr2O7series exhibits the opposite tendency.These results are in agreement with those of previous experiments.

The lattice-constant changes of(Gd2−yUy)Zr2O7and Gd2(Zr2−yUy)O7are related to the difference in the ionic radii change after doping.The latticeconstant changes of(Gd2−yZry)(Zr2−yGdy)O7and (Gd2−yZry)(Zr2−yUy)O7are related to the change in electronegativity of the cation sites that arise from the swapping or doping of atoms.In the case of (Gd2−yZry)(Zr2−yGdy)O7,the Coulomb repulsions between the A-site atoms and the O8b-site increase,and the ionic bond dA−O8bincreases while the Coulomb repulsions are dominant.The covalent bond plays a dominant role in the bond dB−O48f,which increases due to the introduction of atoms with larger ionic radii.The lattice constant of pyrochlore is determined by the shortbond lengths of dA−O8band dB−O48f.Therefore,the lattice parameter obviously increases along with an increase in cation disorder in(Gd2−yZry)(Zr2−yGdy)O7, and a smaller lattice parameter increase is seen in (Gd2−yZry)(Zr2−yUy)O7due to the lower increase in electronegativity at the B site.The radii ratio of the A to B sites(rA/rB)decreases as the cation disorder y in(Gd2−yZry)(Zr2−yGdy)O7increases.Furthermore, the positional parameter xO48fincreases,which indicates greater radiation resistance capability.Finally, uranium is a preferable substitute for the B-site gadolinium atoms in cation-disordered Gd2Zr2O7over the A-site gadolinium atoms in ordered Gd2Zr2O7due to the former’s lower total energy.

V.ACKNOWLEDGMENTS

This work was supported by the General Research Fund Scheme of the Research Grants Council of Hong Kong(No.715612 and No.17206714),the National Natural Science Foundation of China(No.11304254 and No.21101129),and the Key Subject Laboratory Foundation of National Defense for Radioactive Waste Environmental Security of SWUST(No.13zxnk09 and No.13zxnk11).

[1]J.Tollefson,Nature 473,266(2011).

[2]R.C.Ewing,Proc.Natl.Acad.Sci.USA 96,3432 (1999).

[3]K.E.Sickafus,L.Minervini,R.W.Grimes,J.A. Valdez,M.Ishimaru,F.Li,K.J.McClellan,and T. Hartmann,Science 289,748(2000).

[4]B.P.Mandal and A.K.Tyagi,J.Alloys Comp.437, 260(2007).

[5]J.Lian,L.M.Wang,S.X.Wang,J.Chen,L.A.Boatner,and R.C.Ewing,Phys.Rev.Lett.87,145901 (2001).

[6]K.E.Sickafus,R.W.Grimes,J.A.Valdez,A.Cleave, M.Tang,M.Ishimaru,S.M.Corish,C.R.Stanek,and B.P.Uberuaga,Nat.Mater.6,217(2007).

[7]S.Moll,G.Sattonnay,L.Thom´e,J.Jagielski,C. Decorse,P.Simon,I.Monnet,and W.J.Weber,Phys. Rev.B 84,064115(2011).

[8]S.J.Patwe,B.R.Ambekar,and A.K.Tyagi,J.Alloys Comp.389,243(2005).

[9]R.C.Ewing,W.J.Weber,and J.Lian,J.Appl.Phys. 95,5949(2004).

[10]G.Sattonnay and R.T´etot,J.Phys.:Condens.Matter 26,055403(2014).

[11]W.R.Panero,L.Stixrude,and R.C.Ewing,Phys. Rev.B 70,054110(2004).

[12]K.V.G.Kutty,R.Asuvathraman,R.R.Madhavan, and H.Jena,J.Phys.Chem.Solids 66,596(2005).

[13]J.D.S.Walker,J.R.Hayes,M.W.Gaultois,E.R. Aluri,and A.P.Grosvenor,J.Alloys Comp.565,44 (2013).

[14]A.Garbout,B.Bouattour,and A.W.Kolsi,J.Alloys Comp.469,229(2009).

[15]Z.Liu,S.Gao,J.Ouyang,and X.Xia,J.Alloys Comp. 506,868(2010).

[16]J.Lian,L.Wang,J.Chen,K.Sun,R.C.Ewing,J. Matt Farmer,and L.A.Boatner,Acta Mater.51,1493 (2003).

[17]N.K.Kulkarni,S.Sampath,and V.Venugopal,J.Nucl. Mater.281,248(2000).

[18]D.J.Gregg,Y.Zhang,Z.Zhang,I.Karatchevtseva, M.G.Blackford,G.Triani,G.R.Lumpkin,and E.R. Vance,J.Nucl.Mater.438,144(2013).

[19]D.J.Gregg,Z.Zhang,G.J.Thorogood,B.J.Kennedy, J.A.Kimpton,G.Griffiths,P.R.Guagliardo,G.R. Lumpkin,and E.R.Vance,J.Nucl.Mater.452,474 (2014).

[20]M.Parrinello and A.Rahman,Phys.Rev.Lett.45, 1196(1980).

[21]S.H.Vosko,L.Wilk,and M.Nusair,Can.J.Phys.58, 1200(1980).

[22]L.Bellaiche and D.Vanderbilt,Phys.Rev.B 61,7877 (2000).

[23]A.Gueddima,R.Zerdoumb,and N.Bouarissa,Physica B 389,335(2007).

[24]S.Bacha,A.Bechiri,F.Benmakhlouf,H.Allouache, and N.Bouarissa,Physica B 406,2021(2011).

[25]P.Ou,J.Wang,S.Shang,L.Chen,Y.Du,Z.Liu,and F.Zheng,Surf.Coat.Technol.264,41(2015).

[26]B.Ghebouli,M.A.Ghebouli,and M.Fatmi,Physica B 406,2521(2011).

[27]B.P.Mandal,A.Banerji,V.Sathe,S.K.Deb,and A. K.Tyagi,J.Solid State Chem.180,2643(2007).

[28]X.J.Wang,H.Y.Xiao,X.T.Zhu,and W.J.Weber, J.Nucl.Mater.419,105(2011).

[29]J.A.Purton and N.L.Allan,J.Mater.Chem.12,2923 (2002).

[30]Q.Y.Chen,M.Xu,H.P.Zhou,M.Y.Duan,W.J. Zhu,and H.L.He,Physica B 430,1666(2008).

[31]Q.Y.Chen,C.M.Meng,T.C.Lu,M.Xu,J.Q.Qi, and J.J.Tan,J.Appl.Phys.108,113522(2010).

[32]R.D.Shannon,Acta Crystallogr.A 32,751(1976).

[33]W.R.Panero,L.Stixrude,and R.C.Ewing,Phys. Rev.B 70,054110(2004).

[34]J.Lian,L.Wang,R.Haire,K.Helean,and R.C.Ewing, Nucl.Instrum.Methods Phys.Res.B 218,236(2004).

[35]J.Lian,S.V.Yudintsev,S.V.stefanovsky,L.M.Wang, R.C.Ewing,J.Alloys Comp.444-445,429(2007).

[36]S.X.Wang,B.D.Begg,L.M.Wang,R.C.Ewing,W. J.Weber,and K.V.Govidan Kutty,J.Mater.Res.14, 4470(1999).

∗Authors to whom correspondence should be addressed.E-mail: kshih@hku.hk,mcm901570@126.com