One-Dimensional Scanning of Electronic Wavefunction in Carbon Nanotubes by Molecular Encapsulation

Gui Ye,Jun Li,Ming-sen Deng,Jun Jing∗

a.Hefei National Laboratory for Physical Sciences at the Microscale,Collaborative Innovation Center of Chemistry for Energy Materials,School of Chemistry and Materials Science,University of Science and Technology of China,Hefei 230026,China

b.Guizhou Provincial Key Laboratory of Computational Nano-Material Science,Guizhou Normal College,Guiyang 550018,China

(Dated:Received on June 1,2015;Accepted on September 24,2015)

One-Dimensional Scanning of Electronic Wavefunction in Carbon Nanotubes by Molecular Encapsulation

Gui Yea,Jun Lia,Ming-sen Dengb,Jun Jianga∗

a.Hefei National Laboratory for Physical Sciences at the Microscale,Collaborative Innovation Center of Chemistry for Energy Materials,School of Chemistry and Materials Science,University of Science and Technology of China,Hefei 230026,China

b.Guizhou Provincial Key Laboratory of Computational Nano-Material Science,Guizhou Normal College,Guiyang 550018,China

(Dated:Received on June 1,2015;Accepted on September 24,2015)

On the basis of first-principles calculations,we have designed a novel type of molecular systems in which a single-walled carbon nanotube(SWNT)is encapsulated by acyclic CB[n]-type molecular container.The electronic structures and coherent electron transportation properties of the molecules were simulated at the density functional theory level.Due to the weak interactions between the inner SWNT and outer molecular container,the acyclic part can slide along the nanotube direction,which in turn effectively changes the electron tunneling ability through the SWNT.The dependences of tunneling conductance on the position of the acyclic container attached to the SWNT were examined,which reflect clearly a Bloch form distribution of molecular wavefunction along the nanotube direction.We thus proposes a convenient way to scan the one-dimensional electron wavefunction in carbon nanotubes.

Single-walled carbon nanotube,Molecular container,One-dimensionalelectron wavefunction distribution,Density functional theory

I.INTRODUCTION

Owing to the unique physical and chemical properties,carbon nanotube(CNT)based nanostructures have been widely studied and utilized in the past decades.In particular,the one-dimensional(1D)distribution of atomic and electronic structures,quantum interference of electronic states,and quantum confinement effect originated from the finite size have brought about many intriguing properties for CNTs[1−5].Until now,CNTs have been demonstrated as good components for conducting molecular wires,transistors, nanoscale sensors,and nanoelectromechanical devices [6−18].CNTs,especially single-walled carbon nanotubes(SWNTs),hold great promise for gas sensors [6,9−12,14−16].Making use of the modulation of electrical properties by interacting with attached gas molecules,CNT-based sensors can detect various gas molecules,such as NH3,NO2[12],O2[6],SO2[9], NO[11],and H2S[15].Meanwhile,telescoped doublewalled nanotubes(TDWNTs)[16]and multiwalled carbon nanotubes(MWNTs)[10]play a great role in nanoelectromechanical systems,which utilizes the sensitivity of electronic and transport properties to the interactions between the outer and inner shells.Taking advantage of the relationship between the interlayer conductance and the interlayer motion,TDWNTs were used as nanoresonantors[10],nanomechanical switches[18], nanodisplacement sensors[13],nanorheostats[7],and nanomotors[8].

In general,the utilization of CNTs as sensors and nanoelectromechanicalsystems relies on the manipulation of the inter-molecular interactions of other molecules with CNTs,which are decided by the distribution of electronic properties in the tubes.As a 1D nanostructure,the information of electronic wavefunction distributions along the tube direction is very important for finite sized CNT molecular devices.For example,the control of electronic couplings between the outer and inner SWNT shells of a telescoping CNT would benefit from the understanding of the 1D wavefunction distributions in its separated SWNT components.Until now,many efforts have been conducted to reveal the wavefunction distribution in finite sized SWNTs.It was found from tight-binding calculations[1]that SWNTs in finite size often exhibit a Bloch form superimposing on the local wavefunctions,which was soon confirmed by our advanced first-principles study[19].Meanwhile, Liu et al.[13]and Tamura et al.[16]have computed the electronic couplings between the shells of TDWNTs. They both observed the trigonometric function dependence on inter-shell displacement,suggesting the superimposing of the Bloch wavefunction.In experiments, people have applied scanning tunneling microscope (STM)measurements to capture the precise distribution map of wavefunctions in SWNTs[2−5].Unfortunately,the measurement of STM is normally expensive and time-consuming,and its tip can achieve contact with only one position at one time so that it omits the information of the whole carbon cycle.Also,the tunneling current might induce strong local electric field which in turn changes SWNT wavefunction.Another alternative method is to measure the conductance of TDWNTs by sliding the outer shell,which is however questionable as the constant change of overlap area between its two SWNT shells often complicates the measurement and actually deviates the wavefunction from pure Bloch form[7].Therefore,the applications of CNT based molecular devices are in urgent need for a convenient and accurate way to scan the 1D wavefunction distribution in SWNTs.

In this work,we have designed a novel type of molecular systems denoted as AC@SWNT,in which a singlewalled carbon nanotube(SWNT)is encapsulated by an acyclic CB[n]-type(AC)molecular container.The AC container is widely used in nanoscale drug delivery[20].A recent work by Ma et al.has demonstrated the perfect encapsulation of SWNT by an AC container [21],which exhibits good solubility in water and flexible contacting structures.Using the same molecule in that work while removing the edge parts,we encapsulated a(5,5)armchair SWNT with the AC container attaching to a certain position.First-principles simulations were performed to investigate the change of electric currents through SWNT when the AC container was sliding along the tube direction.The density functional theory(DFT)calculations demonstrate the weak couplings between the AC and SWNT,as well as the effective modulation of electron tunneling ability and conductance by sliding AC.We have examined the dependence of tunneling conductance on the position of the AC container,which is found to be originated from the distribution of 1D wavefunction in SWNT.We thus propose a convenient way to scan the 1D electron wavefunction in carbon nanotubes.The information of 1D wavefunction distribution will be of great importance for the future CNT based nanoelectromechanical applications.

II.COMPUTATIONAL METHOD

FIG.1(a)The atomic model(upper)and chemical structure(lower)of the AC molecular container.(b)The atomic model for a(5,5)armchair SWNT.(c)The schematic illustration of the electronic conductance measurement setup for the designed AC@SWNT(5,5)structure(SWNT encapsulated by AC).Here the yellow,blue,purple,and red beads stand for C,H,N,and O atoms,respectively.

The atomic model for the acyclic CB[n]-type molecular container was built in regard to the chemical composition and shown in Fig.1(a).Normally,SWNTs are defined with two chiral vectors of(n,m),based on which the tubes can be categorized into three groups called armchair(n=m),zigzag(m=0),and otherwise chiral.Here we take one of the mostly investigated (5,5)armchair SWNT as a demo system,which is normally metallic with high electric conductivity.From the atomic modelfor the(5,5)SWNT in Fig.1(b),the tube is composed of a series of carbon cycles along the tube direction,in which each cycle is a 10-carbon ring.The distance between two adjacent rings is about 1.23˚A. The AC@SWNT(5,5)structure in Fig.1(c)was built by encapsulating the SWNT with the AC container. We have chosen a(5,5)SWNT with 33 carbon rings as a model system for this study.To avoid the uncertain edge effects in property analysis,we deliberately omitted three carbon rings at both ends ofthe SWNT in the AC sliding simulations.The starting and ending points of AC sliding are at the 4th and 30th carbon rings,and we labeled the scanning positions as L1,L2,···,L27.

FIG.2(a)The computed electron transmission spectra in log scale and(b)conductance-voltage curves for the AC@SWNT(5, 5)system with AC attached to the L3,L9,L15,L21,L27 positions(named as AC@Li).

Geometry optimizations and electronic structure calculations based on molecular models have been performed at the hybrid DFT B3LYP levelwith the 6-31G basis set using Gaussian09 software package[22].By sliding the AC part in the AC@SWNT(5,5),we optimized the molecular geometry.The fact that we could achieve stabilized structures with AC attaching to SWNT from L1 to L27,implies relatively weak interactions between the outer and inner shells of the AC@SWNT(5,5).The optimized distances between the(5,5)SWNT and AC container during AC sliding are close to 4˚A.

Assuming bias voltage at the ends of SWNT and electrons are injected into and flow out through the terminated Hydrogen atoms,we have examined the change of electronic conductance during AC sliding.The electron transportation properties are calculated using the QCME(quantum chemistry molecular electronics)[23] program.The QCME program allows us to collect the electronic structural information from DFT calculations,based on which the charge transmission rate through the SWNT in the AC@SWNT(5,5)is simulated with the Green’s function theory.

III.SIMULATIONS RESULTS

The computed electron transmission spectra for several AC scanning potions at L3,L9,L15,L21,L27 (named as AC@Li)are shown in Fig.2(a).Although armchair SWNTs with infinite size are metallic tubes with high conductivity,our AC@SWNT(5,5)system exhibits quantized tunneling channels,meaning that the (5,5)SWNT with the finite size of 33 carbon rings still holds quantized molecular orbitals.As in Fig.2(a), the primary electron transmission feature are very similar for all of the scanning points,with almost identical transportation peak/channel positions.It is known that the charge transportation channels in a molecular system are originated from its molecular orbitals. This suggests that the slide of AC positions would not change the energy diagrams for molecular orbitals in the AC@SWNT(5,5).Correspondingly,the computed curves of conductance as the function of sourcedrain voltage(VSD)shows the similar features for the AC@L3,AC@L9,AC@L15,AC@L21,AC@L27 systems.In contrast,the intensities of transmission and conductance are sensitive to the change of scanning positions.For most of the conducting peaks,the orders of intensities are AC@L15＞AC@L9＞AC@L3 and AC@L15＞AC@L21＞AC@L27,implying a volcano dependence ofthe conductance on scanning positions from L1 to L27.

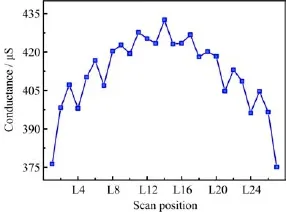
FIG.3 The variation of the first conductance peak intensity with the AC container sliding from L1 to L27 in our AC@SWNT(5,5)system.

Focusing on the first conducting peak in the AC@Li systems,we illustrated the variation of peak intensity with AC sliding from L1 to L27 in Fig.3.The variation region is from 375µS to 435µS,spanning about 15%of the mean absolute values.This demonstrates the sensitivity of electronic conductances to the sliding of the AC part.It is found that the peak intensity value oscillates with a period of 3 carbon rings,which is an intrinsic feature of(5,5)SWNT[19,24].Meanwhile, there is a big wavepacket form superimposing on the conductance-position dependence,which is the typical Bloch feature revealed by previous theoretical studiesfor telescoped DWNT[13,16].Because of the symmetry of Bloch wave,the intrinsic 3-carbon-ring oscillation property was destroyed in the region of L10 to L18,resulting in the highest conductance peak at L14.This means,the Bloch wave form dominants the distribution of wavefunction in the SWNT and thereby decides the couplings with the AC container.

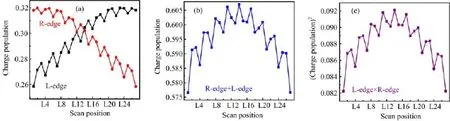
FIG.4 The computed edge charge populations of(a)left edge(L-edge)and right edge(R-edge),(b)charge summation of L-edge+R-edge,and(c)charge product of L-edge×R-edge in the first conducting channel(corresponding to the first peak in the conductance curve)of AC@SWNT(5,5).

IV.DISCUSSION

It is necessary to identify the origin of the conductance variations in different AC@Li systems,which should be ascribed to the change of intermolecular interactions during AC sliding.It is noted that the energy variations induced by AC sliding are actually very small,and Fig.2 also shows an unchanged molecular orbital energy diagrams in different AC@Li systems. These suggest that the encapsulation by AC container does not change the dominant pattern of electron density distribution in the carbon nanotube,which otherwise would cause big differences to the molecular orbital energies.Therefore,by reflecting the coupling of the AC molecule with the electron density of the SWNT at a certain position,the variation of conductance could serve as an accurate reflection of the wavefunction distribution of the nanotube.

Here we can apply the site representation to discuss the factors that decide the tunneling ability and conductance of the molecular system.In general,the tunneling electrons are injected from one of the two edge of the SWNT and flow out through the other one.Based on the Green’s function theory,the tunneling ability depends on the couplings between the edges and electrodes,as well as the edge charge populations in a conducting channel.The edge-electrode couplings are unlikely affected by the weak interactions between the AC and SWNT.The edge populations,on the other hand, could be effectively altered by intermolecular interactions.Defining the edge region as 3-carbon rings in the SWNT,we can compute charge population for the edge parts.Here we still focus on the first conducting channel,which is actually the lowest unoccupied molecular orbital(LUMO)in the AC@SWNT(5,5).The computed left and right edge charge population are plotted in Fig.4(a).It is found that the encapsulation of AC could subtly lower the local charge population of the nanotube at around the attach position,and thereby increase the populations a little at other parts.The summation and product of the left and right charge population are shown in Fig.4(b)and(c),which exhibit the similar global Bloch form and local 3-carbonring oscillation features as the conductance-scanning position curve in Fig.3.Compared to the conductance variations observed in sliding telescoped DWNTs,the conductance and charge population variation curves in our designed AC@SWNT system manifest rigid Bloch wavepacket and strict localoscillation,which agree very well with the experimentally measured 1D wavefunction distribution map by STM[2−5].Therefore,our designed system has provided an accurate scan of the 1D wavefunction along the carbon nanotube.

V.CONCLUSION

In summary,we have employed the acyclic CB[n]-type molecular container to construct a convenient and flexible AC@SWNT encapsulation system.DFT simulations were performed to reveal the electronic properties of the AC@SWNT system.The sensitivity of the electron tunneling ability and conductance to the AC attaching position on SWNT enables us to probe the 1D electronic wavefunction distribution in carbon nanotubes.It is demonstrated that the variation of conductance is ascribed to the change of charge population in a certain conducting channel,as induced by the coupling between the outer and inner shell.These would lead to a convenient way to scan the 1D electron wavefunction in carbon nanotubes,help to understand the fundamental physics in low-dimensional and nanoscale carbon materials,and guide the future design of nano-electromechanical devices.

VI.ACKNOWLEDGMENTS

This work was supported by the National Natural Science Foundation of China(No.91221104),the Fundamental Research Funds for the Central Universities (No.WK2090050027 and No.WK2310000035),the Open Project of Beijing National Laboratory for Molecular Sciences(No.2013002),and the Program for Innovative Research Team of Guizhou Province of China (No.QKTD-[2012]4009),the University Development Fund of Guizhou Province(No.2007063),and the Talent Special Fund of Guizhou Province(No.TZJF-2006328).

[1]M.Furuhashi and T.Komeda,Phys.Rev.Lett.101, 185503(2008).

[2]J.Lee,S.Eggert,H.Kim,S.J.Kahng,H.Shinohara, and Y.Kuk,Phys.Rev.Lett.93,166403(2004).

[3]S.G.Lemay,J.W.Janssen,M.van den Hout,M. Mooij,M.J.Bronikowski,P.A.Willis,R.E.Smalley,L.P.Kouwenhoven,and C.Dekker,Nature 412, 617(2001).

[4]M.Ouyang,J.L.Huang,and C.M.Lieber,Phys.Rev. Lett.88,066804(2002).

[5]L.C.Venema,J.W.G.Wildoer,J.W.Janssen,S.J. Tans,H.L.J.T.Tuinstra,L.P.Kouwenhoven,and C. Dekker,Science 283,52(1999).

[6]P.G.Collins,K.Bradley,M.Ishigami,and A.Zettl, Science 287,1801(2000).

[7]J.Cumings and A.Zettl,Phys.Rev.Lett.93,086801 (2004).

[8]A.M.Fennimore,T.D.Yuzvinsky,W.Q.Han,M. S.Fuhrer,J.Cumings,and A.Zettl,Nature 424,408 (2003).

[9]A.Goldoni,R.Larciprete,L.Petaccia,and S.Lizzit,J. Am.Chem.Soc.125,11329(2003).

[10]K.Jensen,C.Girit,W.Mickelson,and A.Zettl,Phys. Rev.Lett.96,215503(2006).

[11]D.R.Kauffman and A.Star,Nano.Lett.7,1863 (2007).

[12]J.Kong,N.R.Franklin,C.W.Zhou,M.G.Chapline, S.Peng,K.J.Cho,and H.J.Dai,Science 287,622 (2000).

[13]Q.H.Liu,L.L.Yu,H.Li,R.Qin,Z.Jing,J.X.Zheng, Z.X.Gao,and J.Lu,J.Phys.Chem.C 115,6933 (2011).

[14]E.S.Snow,F.K.Perkins,E.J.Houser,S.C.Badescu, and T.L.Reinecke,Science 307,1942(2005).

[15]A.Star,V.Joshi,S.Skarupo,D.Thomas,and J.C.P. Gabriel,J.Phys.Chem.B 110,21014(2006).

[16]R.Tamura,Phys.Rev.B 82,035415(2010).

[17]S.J.Tans,A.R.M.Verschueren,and C.Dekker,Nature 393,49(1998).

[18]Q.M.Yan,G.Zhou,S.G.Hao,J.Wu,and W.H. Duan,Appl.Phys.Lett.88,173107(2006).

[19]B.Gao,J.Jiang,K.Liu,Z.Y.Wu,W.Lu,and Y.Luo, J.Chem.Phys.128,084707(2008).

[20]D.Ma,G.Hettiarachchi,D.Nguyen,B.Zhang,J.B. Wittenberg,P.Y.Zavalij,V.Briken,and L.Isaacs, Nat.Chem.4,503(2012).

[21]C.Shen,D.Ma,B.Meany,L.Isaacs,and Y.H.Wang, J.Am.Chem.Soc.134,7254(2012).

[22]M.J.Frisch,G.W.Trucks,H.B.Schlegel,G.E. Scuseria,M.A.Robb,J.R.Cheeseman,G.Scalmani, V.Barone,B.Mennucci,and G.A.Petersson,Gaussian 09,Revision A.1,Pittsburgh,PA:Gaussian Inc., (2009).

[23](a)J.Jiang,M.Kula,and Y.Luo,J.Chem.Phys.124, 34708(2006). (b)J.Jiang,W.Lu,and Y.Luo,Nano Lett.5,1551 (2005).

[24]J.Jiang,K.Liu,W.Lu,and Y.Luo,J.Chem.Phys. 124,214711(2006).

∗Author to whom correspondence should be addressed.E-mail: jiangj1@ustc.edu.cn,Tel.:+86-551-63600029