Chemical Empiricism 2.0 at Age of Big Data:Large-scale Prediction of Reaction Pathways Based on Bond Dissociation Energies

Shi-lu Chen

Key Laboratory of Cluster Science of Ministry of Education,School of Chemistry,Beijing Institute of Technology,Beijing 100081,China

(Dated:Received on May 20,2015;Accepted on July 26,2015)

Chemical Empiricism 2.0 at Age of Big Data:Large-scale Prediction of Reaction Pathways Based on Bond Dissociation Energies

Shi-lu Chen∗

Key Laboratory of Cluster Science of Ministry of Education,School of Chemistry,Beijing Institute of Technology,Beijing 100081,China

(Dated:Received on May 20,2015;Accepted on July 26,2015)

A programmable algorithm using bond dissociation energies has been proposed for the prediction of reaction pathways.It has been successfully applied to a gas-phase reaction of F2+CH3Cl,with the accurate revelation of the most favorable product CF4and its corresponding reaction pathway.This acts as an inspiring example of chemical empiricism 2.0, and may open the door for the large-scale prediction of reaction pathways at the age of big data.

Big data,Bond dissociation energy,Reaction pathway,Prediction

I.INTRODUCTION

In the past centuries,a large number of chemical empirical methods have been created and worked in various aspects of chemistry[1].They have been and are fruitful for the development of science,even if advancements in modern physics,in particular the development of quantum mechanics(QM),have made it possible to ab initio explore diverse chemical issues.In this age of chemical empiricism 1.0,it was often found that some non-well-theorized empirical formulas,which might be simply derived from limited evidences,work very well in the fields where QM could not perfectly account for yet.Nowadays,with an uncountable number of chemical data accumulated from experiments and theories, coupled with the nearly exponentialgrowth of computer power,we are welcoming chemical empiricism 2.0 at a new age ofbig data,a combination ofchemicalintuition and abundant QMdata(i.e.,QM simulations).Using a simple but well-defined algorithm that originates from chemical intuition,one can today routinely handle systems containing countless QM-derived data,which may open the door for the large-scale prediction in various chemical fields based on big data of QM simulations. On the other hand,the successful prediction based on big data may optimize chemists’intuition,facilitating the development of new chemical methods.

One of the fields that chemical empiricism 2.0 may have positive impact on is the prediction of reaction pathways,which is usually believed to be of high difficulty and only handleable by high-level QM methods. In this work,a simple and programmable algorithm is proposed for the large-scale prediction of reaction pathways,based on bond dissociation energies(BDEs),a type of simple QM-derived data.The BDEs used in the prediction procedure can be easily obtained by automatic calculations using high-level QM methods,such as the density functional theory(DFT).The specific reaction under consideration is a gas-phase reaction of F2+CH3Cl.The algorithm proposed here has been successfully applied to this reaction,in particular accurately revealing the most favorable product(CF4)and its reaction pathway.This demonstrates that the algorithm is capable of predicting pathways of the reactions where radicals are dominant intermediates,and thus acts as a successful example of chemical empiricism 2.0 at the age of big data.

II.PREDICTION ALGORITHM

An algorithm for the prediction of reaction pathways,which is programable,is schematically presented in Scheme 1.

All reactants are first split into fragments by exhaustively enumerative homolysis ofevery chemicalbond[2]. The resultant fragments are referred to as first-order fragments(FOFs).Every molecule/fragment emerging in the prediction algorithm is marked by a unique numerical label.The bond dissociation energy(BDE) corresponding to each homolysis is automatically calculated by high-level QM methods(described later)and recorded with a unique label.Secondly,enumerative coupling among FOFs are performed,leading to a series of products(referred to as first-order products,FOPs). The repeating couplings and the ones back to reactants are omitted.The bond formation energy(BFE)for each coupling is equal to the minus of corresponding BDE and is calculated by the same quantum chemical method.The reaction pathway for the formation ofeach FOP is defined as the corresponding FOF formation via the homolysis of reactants,followed by the coupling of the FOFs.The reaction energy(ΔE)is calculated by the sum of BDEs and BFEs along the reaction pathway.It should be noted that all reaction pathways as well as theirΔE should be regulated to have the same amount of reactants(at least with one reactant as the reference).Then,all reaction pathways are assessed by comparing theirΔE with several criteria.(i)The pathway with the smallestΔE is favorite.(ii)If several pathways are calculated to have significantly negative ΔE,all of them are favorable even though theirΔE are quite different.(iii)The one with smaller BDE of FOFs is preferential whenΔE are close or significantly negative.(iv)When allΔE of FOPs are positive,in principle the selected pathway should not have too big ΔE;otherwise,all reaction pathways should be ruled out.(v)In general only one pathway excels others;if several paths are undistinguishable by the former four rules,all of them are elected.

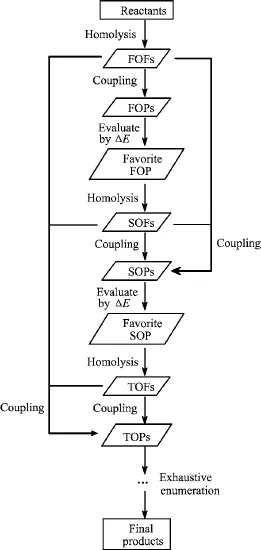
Scheme 1 Schematic algorithm for the prediction of reaction pathways.FOF:first-order fragment.FOP:first-order product.SOF:second-order fragment.SOP:second-order product.TOF:three-order fragment.TOP:three-order product.E:reaction energy.

The subsequent reactions of the favorite FOP follow the same pattern as the case of reactants,i.e.,the breaking of FOP to second-order fragments(SOFs)by exhaustively enumerative homolysis of every chemical bond,followed by the coupling of resultant SOFs with all FOFs as well as SOFs,resulting in second-order products(SOPs).The formation of SOPs is evaluated with their correspondingΔE via the same rules for FOPs(described earlier).The same treatments are then applied to the favorite SOP and the following products until all possible fragments and products derived via the five criteria described above are exhaustively enumerated.

It is worth noting that only thermodynamics is considered in this algorithm.Although it is impossible to estimate reaction rate,the energy barrier in each reaction pathway is to a certain extent dependent on the ΔE,since the raise/drop of product parabola may result in the same shift of the intersection with reactant parabola,thus leading to the increase/decrease of barrier height.This speculation may be quite close to the truth in a displacement reaction where reactant states are the same in many tested pathways,for example,in the specific case of F2+CH3Cl studied here.

All quantum chemical calculations presented in this work were performed using unrestricted DFT with the hybrid functional B3LYP[3−5]as implemented in Gaussian 09 package[6].With dispersion included, geometry optimizations were carried out using the 6-311++G(d,p)basis set.Dispersion corrections were considered using the empirical formula by Grimme et al.(i.e.,DFT-D3)[7−10].BDEs were calculated by:

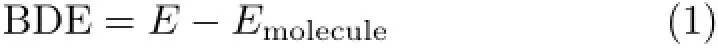
where E is energy sum of separated fragments,while Emoleculeis energy of molecule.In the future calculations of BDEs,more effects,such as temperature,pressure,solvent,and so on,may be introduced to more accurately adapt to complicated gas-phase,liquid-phase, and even heterogeneous reactions.

Furthermore,it willbe valuable to construct a special database to store the BDEs which are collected from reliable experiments and previous QM calculations.The prediction program can directly read the data when the needed BDEs have already been stored in the database. If the BDEs are unavailable,necessary QM calculations will be preformed and the obtained BDEs will be saved in the database in time.This should greatly speed up the prediction of reaction pathways.

III.RESULTS AND DISCUSSION

Using the prediction algorithm described earlier,the reaction of F2+CH3Cl has been analyzed.The formation of first-order products(FOPs)is shown in Fig.1. The calculated BDEs are given in Table I.

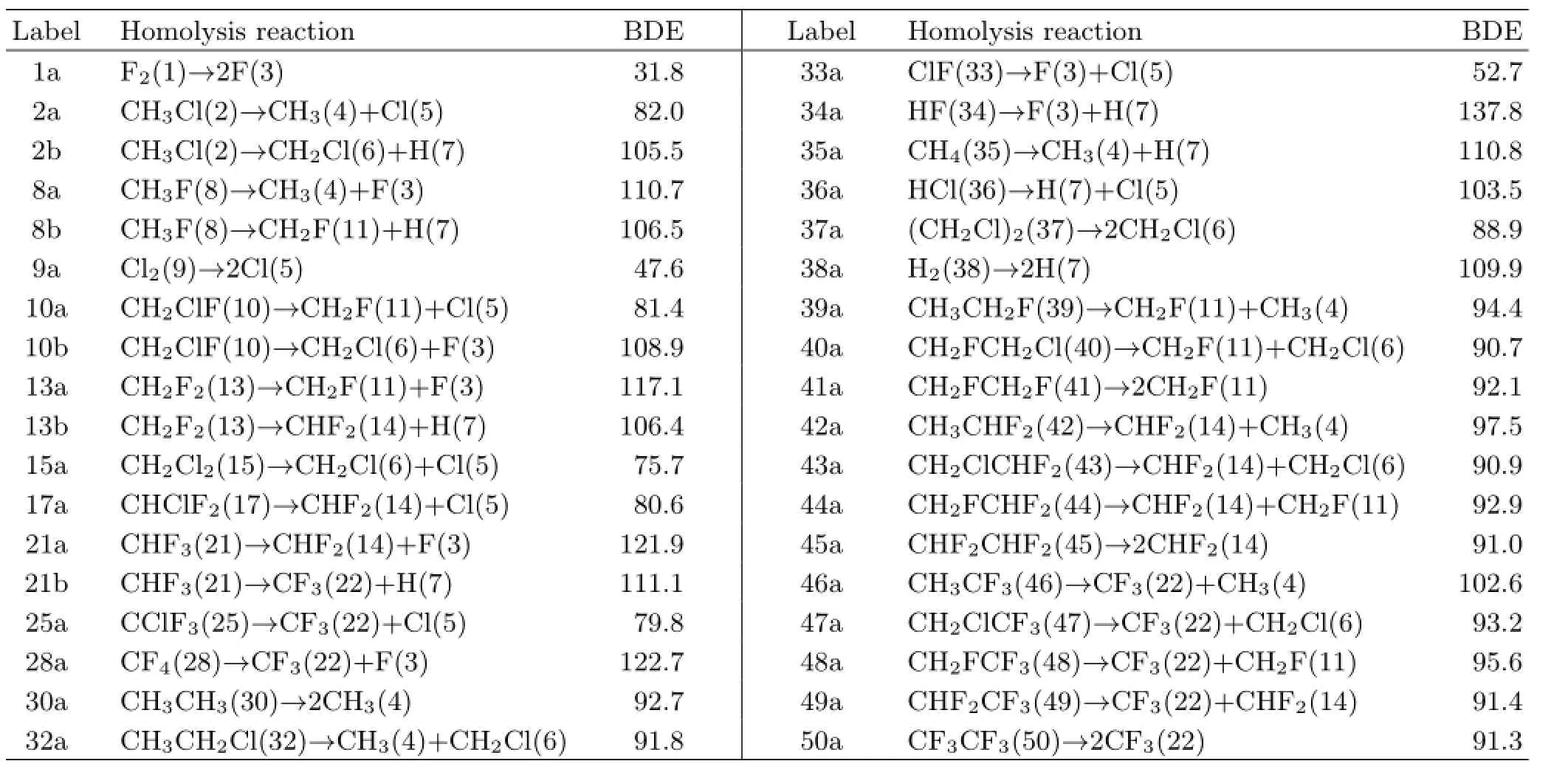
TABLE I Bond dissociation energies(BDEs,in kcal/mol)calculated by B3LYP-D3/6-311++G(d,p).

The F2reactant(labeled by 1)was broken to two F atoms(3)with a BDE of 31.8 kcal/mol(named by 1a), while CH3Cl(2)was separated by two ways,i.e.into CH3(4)+Cl(5)with a BDE of 2a=82.0 kcal/mol and into CH2Cl(6)+H(7)with a BDE of2b=105.5 kcal/mol. The coupling between first-order fragments(3,4,5,6, and 7)were then performed to produce various FOPs with the related reaction energies(ΔE)calculated. Three reactions were found to have significantly negativeΔE.They are

These three reactions were thus predicted to be favorable.In real system,the dissociation of F2to F atoms should be an initial step since its BDE(1a=31.8 kcal/mol)is considerably smaller than those in the CH3Cl homolysis(2a=82.0 kcal/mol and 2b=105.5 kcal/mol).The resultant F atom may attack CH3Cl through three ways.The attack of F on the carbon of CH3Cl should initiate a SN2-type displacement to produce CH3F+Cl or CH2ClF+H,while the attack on the hydrogen of CH3Cl leads to HF+CH2Cl. Subsequently,the homologous coupling of the resulting radicals(Cl,H,and CH2Cl)may take place to form another products in these three reactions(Cl2,H2,and CH2ClCH2Cl).With this,it can be concluded that the present algorithm gives a reasonable prediction for the formation of FOPs in this particular case of F2+CH3Cl.

A further analysis on the formation of FOFs indicates that reaction(R8)costs the smallest energy in the step of FOF formation,compared with reactions(R10)and(R34).The cost energies are 97.9 kcal/moland 121.4 kcal/molfor reactions(R8),(R10), and(R34),respectively.This implies that reaction(R8) may be the favorite one although itsΔE is the highest among these three reactions.This predicted result is consistent with chemical common sense.The corresponding reaction pathway for reaction(R8)is formulated as

FIG.1 Reaction pathways for the formation of first-order products.The labels below arrows indicate bond dissociation energies.

The FOPs of the favorite reaction(R8)(i.e.,CH3F and Cl2)were included in the following formation of second-order fragments and products.The breaking of Cl2can be further omitted since it is actually a reverse process of the Cl2formation.Therefore,only CH3F(8)was considered as the reacting FOP in the subsequent calculations of the formation of SOPs(see Fig.2).CH3F(8)was dissociated to CH2F(11)+H(7) with a BDE of 8b=106.5 kcal/mol or to CH3(4)+F(3) with a BDE of 8a=110.7 kcal/mol.The latter can be omitted because it is a reverse reaction back to the firstorder product of CH3F(8).In addition,considering that the fragment of H(7)is not a new species but a FOF, only the SOF of CH2F(11)was involved in the next coupling of fragments.The coupling of CH2F(11)were carried out with every FOF and then SOF.The reverse and repeating processes were excluded.It has been found that,with CH3F(8)as the reactant state,the favorite reaction for the SOP formation is

FIG.2 Reaction pathways for the formation of second-order products from the favorite first-order product(CH3F).

FIG.3 Reaction pathways for the formation of three-order products from the favorite second-order product(CH2F2).

ItsΔE is much lower than those of other reactions,at least by 40.2 kcal/mol.The corresponding pathway for reaction(R13)is written as

Since H2(38)or H(7)is again a first-order product or fragment,only the second-order product of CH2F2(13) was chosen as the reactant state for the formation of three-order products(TOPs)(see Fig.3).Following the same pattern as the dissociation of CH3F(8),the separation of CH2F2(13)to CH2F(11)+F(3),a reverse process,was skipped,while the one to CHF2(14)+H(7) was kept.Again,only the three-order fragment(TOF) of CHF2(14)was selected for the subsequent coupling as H(7)is a first-order fragment.The combination of CHF2(14)with every FOF,SOF,and then TOF reveals the preferred reaction for the formation of TOPs, The corresponding pathway from CH2F2(13)is formulated as

FIG.4 Reaction pathways for the formation of fourth-order products from the favorite three-order product(CHF3).

The resultant three-order product of CHF3(21)then worked as the reactant state for the formation offourthorder products(OOPs)(Fig.4).CHF3(21)was decomposed to CHF2(14)+F(3)or CF3(22)+H(7).Again, only the fourth-order fragment(OOF)of CF3(22)was used in the next step of coupling with FOFs,SOFs, TOFs,and OOFs.The favorite reaction for the formation of OOPs was found to be

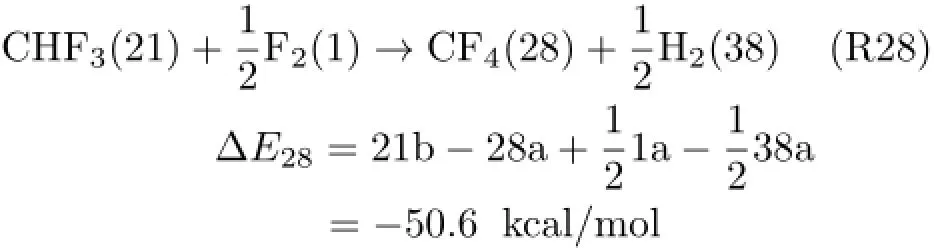
Its related pathway from CHF3(21)is:

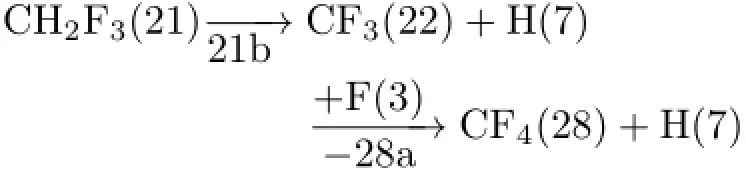
It can be seen that,after four-order treatments,the most favored product in overall reaction of F2+CH3Cl was predicted to be CF4(28),a very reasonable result that is consistent with the chemical fact.This indicates that the present algorithm is competent for the prediction of reaction pathways of the reactions where gas-phase radicals may be dominant intermediates.The complete pathway for the formation of the favorite CF4(28)is summarized in Fig.5.

The overall reaction for the CF4formation is devised as

FIG.5 The complete pathway for the formation of the favorite CF4(28).

If homologous coupling between the radicals of F,H, and Cl are performed,the favorite overall reaction can be written as

With three BDEs(2(1a),(−3/2)38a,and(−1/2)9a) added,the corresponding overall reaction energy(ΔE) for the CF4formation is further calculated to be−191.4 kcal/mol,indicating that it is an energetically reachable reaction.

IV.CONCLUSION

In this work,a programmable algorithm for the prediction of reaction pathways has been proposed,based on the big data of bond dissociation energy(BDE).Combined with the DFT calculations of BDEs,it succeeds in the prediction of the reaction of F2+CH3Cl, successfully revealing the most favorable product(CF4) and its corresponding reaction pathway.This demonstrates that the algorithm is competent for the treatment of gas-phase reactions where radicalintermediates dominate.The exploration here provides an inspiring example of chemical empiricism 2.0,and may open the door for the large-scale digital prediction of reaction pathways at the age of big data.With more techniques introduced,this algorithm may be available for more complicated reactions,such as the ones involving unsaturated bonds and chemical addition steps.If catalysts are regarded as a kind of reactant states,the algorithm may also be developed to be applicable to the catalysis, an exceedingly attractive future.

V.ACKNOWLEDGMENTS

The author thanks Prof.Yi Luo,Prof.Jun Jiang, Dr.Hao Ren,Dr.Wen-hua Zhang,Dr.Feng Zhang, and Dr.Yue-jie Ai for valuable discussions.This work was supported by the National Natural Science Foundation of China(No.21373027),the Beijing Nova Program(No.Z151100000315055),and the 111 Project (No.B07012).

[1]https://en.wikipedia.org/wiki/Empiricism

[2]R.G.A.Bone and H.O.Villar,J.Comput.Chem.18, 86(1997).

[3]A.D.Becke,J.Chem.Phys.98,1372(1993).

[4]A.D.Becke,J.Chem.Phys.98,5648(1993).

[5]C.T.Lee,W.T.Yang,and R.G.Parr,Phys.Rev.B 37,785(1988).

[6]M.J.Frisch,G.W.Trucks,H.B.Schlegel,G.E. Scuseria,M.A.Robb,J.R.Cheeseman,G.Scalmani, V.Barone,B.Mennucci,G.A.Petersson,H.Nakatsuji,M.Caricato,X.Li,H.P.Hratchian,A.F.Izmaylov,J.Bloino,G.Zheng,J.L.Sonnenberg,M. Hada,M.Ehara,K.Toyota,R.Fukuda,J.Hasegawa, M.Ishida,T.Nakajima,Y.Honda,O.Kitao,H.Nakai, T.Vreven,J.A.Jr.Montgomery,J.E.Peralta,F. Ogliaro,M.Bearpark,J.J.Heyd,E.Brothers,K.N. Kudin,V.N.Staroverov,R.Kobayashi,J.Normand, K.Raghavachari,A.Rendell,J.C.Burant,S.S.Iyengar,J.Tomasi,M.Cossi,N.Rega,J.M.Millam,M. Klene,J.E.Knox,J.B.Cross,V.Bakken,C.Adamo, J.Jaramillo,R.Gomperts,E.Stratmann,O.Yazyev, A.J.Austin,R.Cammi,C.Pomelli,J.W.Ochterski, R.L.Martin,K.Morokuma,V.G.Zakrzewski,G.A. Voth,P.Salvador,J.J.Dannenberg,S.Dapprich,A. D.Daniels,¨O.Farkas,J.B.Foresman,J.V.Ortiz,J. Cioslowski,and D.J.Fox,Gaussian 09,Revision D.01, Wallingford CT:Gaussian,Inc.,(2009).

[7]S.Grimme,J.Comput.Chem.25,1463(2004).

[8]S.Grimme,J.Comput.Chem.27,1787(2006).

[9]S.Grimme,J.Antony,S.Ehrlich,and H.Krieg,J. Chem.Phys.132,154104(2010).

[10]L.Goerigk and S.Grimme,Phys.Chem.Chem.Phys. 13,6670(2011).

∗Author to whom correspondence should be addressed.E-mail: shlchen@bit.edu.cn