Importance of Metal Cations and Water for Stability of MnO2Crystals

Zhi-gng Wei,Ji-hong Yn,Yng Wu,Yue Liu

a.Schoolof Chemical Engineering and Light Industry,Guangdong University of Technology,Guangzhou 510006,China

b.Institute of Theoretical Chemistry,Jilin University,Changchun 130023,China

c.College of Chemistry,Liaoning University,Shenyang 110036,China

(Dated:Received on April 13,2015;Accepted on May 18,2015)

Importance of Metal Cations and Water for Stability of MnO2Crystals

Zhi-gang Weia,b∗,Jia-hong Yana,Yang Wuc,Yue Liua

a.Schoolof Chemical Engineering and Light Industry,Guangdong University of Technology,Guangzhou 510006,China

b.Institute of Theoretical Chemistry,Jilin University,Changchun 130023,China

c.College of Chemistry,Liaoning University,Shenyang 110036,China

(Dated:Received on April 13,2015;Accepted on May 18,2015)

Metalcations as well as water are important factors to control the synthesis of MnO2crystal nanostructures.In this work,systemic Density functional theory calculations aboutα,β, δ-MnO2are presented to show the importance of metal cations and water for the structure stability and energy stability of MnO2.It is shown that theα-MnO2crystal and its(110) surface willcrash without the tunnel cations such as K+,and the distance between the layers of theδ-MnO2will be significantly lower than that of the experimental results without the interlayer metal cations and water.At the same time,α-MnO2andδ-MnO2can be more stable thanβ-MnO2with metal cations and water,and vice versa.

MnO2,Density functional theory,Metal cation,Formation energy,Structure simulation

I.INTRODUCTION

MnO2is a very useful material.It has more than 30 different crystal structures[1,2],and can act as electrode,supercapacitor,catalyst,ion sieve,adsorbent, etc.[3−7].In recent years,we tried to control the synthesis of nanostructured manganese oxide with different forms such asα,β,γ,δ,and improve their catalytic properties[8−12].Based on these researches,we found that metal cations as well as water are important factors to control the synthesis of MnO2crystal nanostructures.For example,by using MnSO4and KClO3as starting materials under hydrothermalconditions,when there are sufficient K+and H+,α-MnO2is the product; when there is no K+and H+,γ-MnO2is the product; when there is only H+,β-Mn O2is the product;when there is no H+but Ac−,Mn OOH is the product[8].It is obvious that metal cations and water are necessary to prevent collapse for large framework MnO2such as romanechite,todorokite,etc.[1].In fact,these phenomena have alrealy been reported.In 1998,Fritsch et al.reported that the cations in the crystal tunnels were very important for the stability of MnO2crystals and without the tunnel cations large framework MnO2can not possibly be prepared[13].In 2006,Johnson et al.demonstrated that the interlayer water is strongly bound to the interlayer cations,and plays an important role in the thermal stability of layered MnO2structures [14].

To my knowledge,there has not been a systemic theoretical study about the structure stability and energy stability of MnO2,which corresponds to the metal cations and water in it.In the present work,we just take the frameworkα-MnO2(2×2 tunnel with metal cation K+),β-MnO2(1×1 tunnel without metal cation),and layer structureδ-MnO2(1×∞with and without metal cations and water)as examples to show the importance ofthe metalcations and water by the density functional theory(DFT)calculations.

II.METHODS

The calculations have been performed with DFT with periodic boundary conditions[15].The exchangecorrelation interaction is treated within the generalized gradient approximation(GGA)with the functional parameterized by Perdew,Burke and Enzerhof(PBE) [16].Atomic basis sets are applied numerically in terms of a double numerical plus polarization function with a global orbital cutoff of 4.7˚A[17].The geometry optimization convergence tolerances of the energy,gradient, and displacement are 10−5Hartree,2×10−3Hartree/˚A, and 5×10−3˚A,respectively.All electron DFT calculations in the present work are performed using a DMol3package in the Materials Studio(version 5.5)[18−20]at the same leveloftheory except the different Monkhorst-Pack k points[21]used for the different supercellcalculations.

It is known that the hybrid and the PBE+U methods can give better electronic properties.However,we need to choose different U and different hybrid functionals for different MnO2crystals as well as their sur-faces.As a result,we can not compare the energies based on different calculation parameters as listed in Table I.Therefore,here we mainly list the results from PBE method as the calculations of Oxford et al.[15]. Some calculations are done with the PEB+U methods as listed in the supplementary material.It should be noted that the PBE+U methods gave the same conclusions about the MnO2structures,as presented in the later sections,such as the crash ofα-MnO2and the small layer spacing ofδ-MnO2.Further studies about the optical properties,the conductivities,and the electronic structures are still needed for the MnO2system by the DFT+U and/or the hybrid methods.

III.RESULTS AND DISCUSSION

A.Calculations ofα-MnO2

Theα-MnO2crystal structures can be found from XRD pattern JCPDS No.44-0141 with the lattice constants of a=b=9.8521˚A and c=2.8647˚A.When we calculatedα-MnO2with the supercell Mn8O16using the I4/m symmetry,the results were a=b=9.8688˚A and c=2.8816˚A,which agreed with the experimental results and the computational results of Cockayne et al. [22].Whereas,when we calculated the same supercell without symmetry limit,it crashed as shown in Fig.1(a) (the crash also happened with the PBE+U methods as listed in the supplementary material).It is interesting because K+were visible in the X-ray experiment (JCPDS No.44-0141)and noα-MnO2has been synthesized without tunnel cations[13].It means that K+should be in the supercell.So we added two K+cations to the supercell in the ideal tunnel cation positions such as(0,0,0)and(0.5,0.5,0),and calculated it again.There was no such crash in the supercell,the K+cations were still in their ideal position,their positive charges should be balanced by all the MnO6octahedrons in the tunnel and there was a small distortion in the MnO6octahedrons as shown in Fig.1(b).The symmetry of the optimized structure was close to I4/m and the lattice constants were a=9.8410˚A,b=9.8939˚A, and c=2.9294˚A,and the angles wereα=β=90.0◦and γ=90.3◦.Then,we simulated the supercell with one K+in the ideal tunnelcation position(0.5,0.5,0).The symmetry of the optimized structure was close to P4/m and the lattice constants were a=9.9361˚A,b=9.8660˚A and c=2.9113˚A,and the angles wereα=β=γ=90.0◦. It is clear that K+cations would make the cell large and suppport the 2×2 tunnel without crashing.The larger lattice constants agreed with the X-ray results of natural minerals such as hollandite,cryptomelane,and priderite[23].

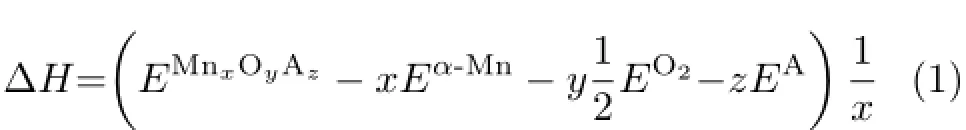
FIG.1 The optimized MnO2crystals,where the O2−ions are shown in red,the spin up and down Mn4+cations are in lavender and green,the K+,Zn2+,and H+cations are in brown,blue and white,respectively. (a)Theα-MnO2without metal cations,(b)theα-MnO2K0.25MnO2,(c,d)the(110)surface ofα-MnO2without and with metal cations,(e)theβ-MnO2,(f)the defect free δ-MnO2,(g)the defectδ-Mn0.96875O2H0.125,and(h)the defectδ-Zn0.25Mn0.75O1.75·0.75H2O.

After the structure simulations,we calculated the formationΔH[15,24,25]as the following in which EMnxOyAz,Eα-Mn,EO2,and EAwere the DFT total energies for MnxOyAz,theαphase of bulk Mn, the oxygen molecule O2and the possible compositions in MnO2crystals such as K+,Na+,Ba2+,respectively. x,y,z and the subscripts x,y,z denoted the number of Mn,O,and K,respectively.The DFT total energy of manganese metal was calculated for collinear anti-ferromagnetic(AFM)α-Mn using GGA optimized lattice constants as Hobbs et al.[26]and Oxford et al. [15]with the Monkhorst-Pack k points 4×4×4 in the Mn58supercell[21].For the DFT total energy of O2, we added 0.451 eV per molecule to correct the overestimation from the DFT calculations[15,24,25,27]. From Table I,the formationΔH of KO.25MnO2(calculated from K2Mn8O16supercell)was−5.965 eV,which was larger than that of−5.601 eV from KO.125MnO2(calculated from KMn8O16supercell).These results agreed with the experimental result of−5.745 eV for KO.3MnO2·0.15H2O(with−5.387 eV in Ref.[24]and−34.5 kJ/mol in Ref.[13])and the experimental trend that more metal cations could make theα-MnO2crystal more stable[13].Based on these simulations we can explain that sufficient K+is an essentialprerequisite for synthesis of theα-MnO2crystal[8].

TABLE I Comparison of the MnO2formationΔH.

The crash ofα-MnO2also happened on its surface such as the(110)surface.When we simulated the surface without K+cations,the structure would crash as shown in Fig.1(c).When the K+cations were added, the surface would be stable as shown in Fig.1(d).It should be noted that we fixed the bottom layer and relaxed the top 3 layers with the supercell of K4Mn16O32. When we added an oxygen molecule to this surface,the adsorption energy was 1.218 eV,the distance between the surface Mn4+cation and O2was 2.2601˚A,the O−O bond of O2extended from 1.2423˚A to 1.2501˚A.

B.Calculations ofβ-MnO2

When we used the Monkhorst-Pack k points 4×4×7 in theβ-MnO2supercell Mn O2O4,the AFM state was found to be the ground state as shown in Fig.1(e),which was 108.7 and 543.0 meV per formula unit lower in energy than that of the ferromagnetic(FM)and nonmagnetic(NM)states,respectively.These magnetic results agreed with the experimental magnetic results[28]and the previous calculations from Oxford et al.[15],that the AFM state was 97 and 648 meV per formula unit lower in energy than that of the FM and NM states.At the same time,the optimized lattice constants of AFM β-MnO2such as a=4.4494˚A,b=4.4345˚A,c=2.8773˚A, α=β=γ=90.0◦were very close to the experimental results[29]a=b=4.4041˚A and c=2.8765˚A and the previous theoretical results[15]a=b=4.4569˚A and c=2.8823˚A.

Calculations about theβ-MnO2crystal were done by different groups with the PBE,PBE0,B3LYP,HSE and PBE+U methods[15,24,30].Detail comparisons between these methods were made by Franchini et al.[24] and Tompsett et al.[30].Based on their calculations and our results,the standard PBE method used in the present work could give good optimized structures but a systematic correction was needed to evaluate the formation.The systematic error came from the calculations of MnO2,α-Mn,and O2,and this correction was applied in all the previous calculations[15,24,25].Comparison of the formation from our PBE calculation with the experimentalformationΔH(−5.387 eV)in Ref.[24]indicated a correction of 0.451 eV per oxygen molecule. The 0.451 eV correction was smaller than that of 0.6, 0.90,and 1.15 eV in Refs.[24,15,25]respectively.In the present work,we tookβ-MnO2crystalas the benchmark for all the MnO2calculations,i.e.,0.451 eV was applied to all the formationΔH quoted,as listed in Table I.

C.Calculations ofδ-MnO2

The simulation results of the layer structureδ-MnO2are shown in Fig.1(f)and(g).In 2008,Kwon et al. published the computational results about vacancy-free and Mn4+defectδ-MnO2[31].Their calculations provided the first direct evidence that such Mn4+defects could indeed facilitate photoconductivity by reducing the band-gap energy and separating electron and hole states.Based on our calculations,we could also see that the Mn4+defect could separate the electron and hole states,and reduce the band gap from 0.9 eV to 0.5 eV;these results were smaller than 1.3 eV to 0.9 eV from Kwon et al.[31].However,there were still two differences.The first issue was about the lattice constant c(Kwon et al.fixed the c/2 to be 7.0005˚A[31]), even if the other lattice constants a and b were similar and the MnO2layer structures were almost the same.From Fig.1(f)and(g),the interlayer spacings(c/2)of the vacancy-free and defect MnO2with the supercells Mn32O64and Mn31O64H4were 5.1505 and 5.1351˚A, respectively.It is known that the interlayer spacing could be tuned by incorporation of large molecules between the layers.

Post reported that the fresh Na-birnessite could change the interlayer spacing from 10˚A to 7˚A by drying and this process is irreversible[1].They also proved that the large metal cations such as Ce cation could extend the interlayer spacing to 7.5135˚A[32].Ching et al.reported that reactions between NaMn O4and glucose yielded two related Na-δ-MnO2products with 5.5 and 7˚A interlayer distances[33].The 5.5˚A Na-δ-MnO2was identified as a dehydrated layered material which could be converted to 7˚A Na-δ-MnO2upon hydration.Based on these reports,the models in Fig.1(f) and(g),which had no cations and water between the layers,should give a lower interlayer spacing than that of 5.5˚A from Ching et al.[33].Therefore,the small interlayer spacings 5.1505 and 5.1351˚A should more closely agree with the experimental results.More tests about the interlayer spacing were made and listed in the supplementary material.It should be noted that the smallinterlayer spacings were confirmed for theδ-MnO2with different calculation methods.The second divergence was about the formationΔH as listed in Table I. From Eq.(1)the formationΔH of defect-free and defectδ-MnO2were−4.932 and−5.019 eV respectively, which were about 0.4 eV higher than that of−5.387 eV fromβ-MnO2.However,Fritsch et al.reported that the formationΔH ofδ-MnO2were 0.713 eV lower than that of theβ-MnO2at 298 K[13].

To achieve a deeper understanding of the structure and formationΔH ofδ-MnO2,the hexagonal chalcophanite(ZnMn3O7·3H2O)was simulated with 6 units in one supercell as shown in Fig.1(h).The optimized lattice constants a and b were both 7.6042˚A,which were a little larger than that of the experimentalresults a=b=7.533˚A[29].Whereas the interlayer spacing (c/3)7.9192˚A was larger than that of the experimental result c/3=6.931˚A[34].On the contrary,when there was less water in the model such as ZnMn3O7·H2O,the interlayer spacing was 7.0780˚A,and the lattice constants a and b were 7.6617 and 7.6626˚A,respectively. The formationΔH were−5.954 and−5.461 eV for ZnMn3O7·3H2O and ZnMn3O7·H2O,respectively as listed in Table I(the result ofβ-MnO2was−5.387 eV). These results agree with the experimental results that δ-MnO2are more stable than theβ-MnO2at 298 K [13],and also support that the interlayer water is strongly bound to the interlayer cations,and plays an important role in the thermal stability of layered MnO2structures[14].

IV.CONCLUSION

In summary,based on the same kind of DFT method, different MnO2crystals such asα,β,δ-MnO2have been simulated.It was shown that metal cations as well as water were very important for the structural stability and energy stability of large tunnel structureα-MnO2(2×2 tunnel)and layer structureδ-MnO2(1×∞),therefore these factors can controlthe synthesis ofmanganese oxides.The importance of metal cations and water should be taken good care of during both the experiments and theoretical simulations.

Supplementary materials:The calculation results of MnO2by different computational methods such as PBE,PBE+U,etc.are given.

V.ACKNOWLEDGMENTS

We thank Ed Goldstraw from the Guangdong University of Technology for helpful discussion.This work was supported by the National Natural Science Foundation of China(No.20703021,No.20803014, and No.21373104)and the 211 Pro ject of Guangdong Province.

[1]J.E.Post,Proc.Natl.Acad.Sci.USA 96,3447(1999).

[2]J.E.Post and D.A.Mckeown,Am.Mineral.86,701 (2001).

[3]Y.L.Lu,L.Yang,M.Wei,Y.Xie,and T.Liu,J.Solid State Electrochem 11,1157(2007).

[4]O.Ghodbane,J.L.Pascal,and F.Favier,ACS Appl. Mater.Inter.1,1130(2009).

[5]C.Wang,L.Sun,Q.Q.Cao,B.Q.Hu,Z.W.Huang, and X.F.Tang,Appl.Catal.B 101,598(2011).

[6]Q.Feng,H.Kanoh,and K.Ooi,J.Mater.Chem.9,319 (1999).

[7]D.L.Zhao,X.Yang,H.Zhang,C.L.Chen,and X.K. Wang,Chem.Eng.J.164,49(2010).

[8]M.Sun,B.Lan,T.Lin,G.Cheng,F.Ye,L.Yu,X. L.Cheng,and X.Y.Zheng,CrystEngComm 15,7010 (2013).

[9]M.Sun,B.Lan,L.Yu,F.Ye,W.Song,J.He,G.Q. Diao,and Y.Y.Zheng,Mater.Lett.86,18(2012).

[10]B.Lan,M.Sun,T.Lin,G.Cheng,L.Yu,S.M.Peng, and J.Xu,Mater.Lett.121,234(2014).

[11]B.Lan,L.Yu,T.Lin,G.Cheng,M.Sun,F.Ye,Q.F. Sun,and J.He,ACS App.Mater.Inter.5,7458(2013).

[12]J.L.Zhou,L.Yu,M.Sun,F.Ye,B.Lan,G.Q.Diao, and J.He,J.Solid State Chem.198,371(2013).

[13]S.Fritsch,J.E.Post,S.L.Suib,and A.Navrotsky, Chem.Mater.10,474(1998).

[14]E.A.Johnson and J.E.Post,Am.Mineral.91,609 (2006).

[15]G.A.E.Oxford and A.Chaka,J.Phys.Chem.115, 16992(2011).

[16]J.P.Perdew and Y.Wang,Phys.Rev.B.45,13244 (1992).

[17]N.A.Benedek,I.K.Snook,K.Latham,and I. Yarovsky,J.Chem.Phys.122,144102(2005).

[18]B.Delley,J.Chem.Phys.92,508(1990).

[19]B.Delley,J.Chem.Phys.100,6107(1996).

[20]B.Delley,J.Chem.Phys.113,7756(2000).

[21]H.J.Monkhorst and J.D.Pack,Phys.Rev.B 13,5188 (1976).

[22]E.Cockayne and L.Li,Chem.Phys.Lett.544,53 (2012).

[23]J.E.Post,R.B.V.Dreele,and P.R.Buseck,Acta Cryst.B 38,1056(1982).

[24]C.Franchini,R.Podloucky,J.Paier,M.Marsman,and G.Kresse,Phys.Rev.B 75,195128(2007).

[25]D.A.Tompsett,S.C.Parker,and M.S.Islam,J.Am. Chem.Soc.136,1418(2014).

[26]D.Hobbs,J.Hafner,and D.Spiˇs´ak,Phys.Rev.B 68, 014407(2003).

[27]S.Fritsch and A.Navrotsky,J.Am.Ceram.Soc.79, 1761(1996).

[28]H.Sato,T.Enoki,M.Isobe,and Y.Ueda,Phys.Rev. B 61,3563(2000).

[29]A.A.Bolzan,C.Fong,B.J.Kennedy,and C.J. Howard,Aust.J.Chem.46,939(1993).

[30]D.A.Tompsett,D.S.Middlemiss,and M.S.Islam, Phys.Rev.B 86,205126(2012).

[31]K.D.Kwon,K.Refson,and G.Sposito,Phys.Rev. Lett.100,146601(2008).

[32]C.L.Lopano,P.J.Heaney,and J.E.Post,Am.Mineral.94,816(2009).

[33]S.Ching,D.J.Petrovay,M.L.Jorgensen,and S.L. Suib,Inorg.Chem.36,883(1997).

[34]J.E.Post and D.E.Appleman,Am.Mineral.73,1401 (1988).

∗Author to whom correspondence should be addressed.E-mail: weizg2003@126.com