关于曲面积分求解的探讨

左岚

(咸宁职业技术学院，湖北 咸宁 437100)

0 引言

高等数学涉及的范围特别广，其中微积分是常见的高等数学知识中最为关键的一个分支，我们常见的是一维方程的微积分。然而，对于想接受更高级别教育体系学习的学生来说，必须要掌握二维方程的微积分，这对于以后的学习以及考研来说是非常重要的。在二维方程的微积分的学习中，其中关于曲面方程的积分的求解是教学和学习的重点难点，对于曲面方程积分求解方法的探讨，尤其是对第二类曲面积分求解方法的探讨，不仅能够深入学习曲面方程积分的特性，对曲面积分有更深入的了解，而且能够提高学生们对曲面积分的求解技巧，从而有助于更加深入地学习其他更加复杂的方程微积分的求解。所以对于曲面方程的积分求解方法的探讨，对于学生学习和考研来说具有非常重要的现实意义。

1 曲面积分的定义和解题技巧

关于曲面积分的定义，具体说明如下:

假定一个函数R(x，y，z)为一个光滑而且有方向的曲面Σ 的某个有固定边界的区域，将Σ 划分成任意的小块，如果每个小块用ΔSi表示(其中i = 1，2，3……，n)，则ΔSi所有的曲面相加等于整个Σ。假设ΔSi在底面x-0-y 轴上的垂直投影为(ΔSi)xy，∀(ξi，ηi，ζi)∈(ΔSi)xy，并且各个小曲面ΔSi的直径λ 趋于0 时，则有如下存在，那么此时，处在光滑的有向曲面Σ 的函数R(x，y，z)在对底面x-0-y 坐标轴的积分称之为第二类曲面积分，一般表示为。同样的，该函数对其他面的第二类曲面积分也可以同样的形式表示，如对于x-0-z 面的第二类曲面积分表示为;对于y-0-z 面的第二类曲面积分表示为。

对第二类曲面积分类型的题目的计算，是在教学工作中以及考研题目中常见的题目类型。对于该类型题目的计算，一般要通过利用第二类曲面积分的基本性质来简化原有题目中的计算表达式，将计算表达式化繁为简、化难为易，从而最终实现第二类曲面积分题目的计算。

常见的，我们在计算第二类曲面积分题目的时候有三个解题技巧:第一个解题技巧是利用第二类曲面积分的可以将曲面积分直接代入到被积分函数中的性质，将曲面方程直接带入到计算表达式中进行积分操作，从而简化计算工作量。例如，假设有球面方程x2+ y2+ z2= R2，其中Σ 为该球面方程的下半球面的上侧部分，则对如下球面积分方程I =进行求解时即可使用该方法，首先将表达式中的x2+ y2+ z2变换成R2之后再找其他适合的方法进行求解。第二个解题技巧则是利用第二类曲面积分的轮换对称性来简化计算表达式，从而简化计算工作量。例如有一曲面x+y+z = 1，Σ 为被x-y-z 坐标轴截取该曲面的下部分的上侧曲面，对于曲面积分xzdxdz 的计算，就可以利用曲面积分的轮换对称性，如果将平面x + y + z = 1 的三个坐标轴的位置任意调换，曲面Σ 的表达式以及被积分的表达式均不发生变化，那么即可利用第二类曲面积分的轮换对称性，即有，则原有的曲面积分计算表达式则可以变换为I =等价于等价于，然后对进行曲面积分即可。第三个解题技巧则是利用了奇函数或者偶函数在第二类曲面积分对称积分面上的基本性质来进行对计算表达式的处理。利用该性质来对第二类曲面积分进行求解时，要求曲面Σ 必须是对称的，并且被积分的函数是奇函数或偶函数。所以在对第二类曲面积分的题目进行解题时，必须注意利用上述解题技巧来简化计算表达式，优化解题过程。

2 曲面积分的求解方法

对第二类曲面积分类型的题目的求解，有很多解题技巧，一般都是通过曲面积分的基本性质来对计算表达式进行简化处理，然后根据简化后的被积分函数进行简体，从而优化解题思路，简化解题过程。当然，解题技巧是死的，必须由解题者对计算表达式能够深刻认识和理解，根据表达式的表现形式进行处理，最终对解题技巧进行灵活运用。在此，对几种常见的第二类曲面积分的解题方法进行阐述说明。

2．1 公式法

利用公式来求解第二类曲面积分的求解方式是最直接有效的方法，即依据第二类曲面积分的定义，通过曲面的投影将计算表达式化解成二重积分来进行计算。

例如，对于Σ 曲面方程为z = z(x，y)，该曲面在x-0-y 面上的投影为Sxy，并且曲面Σ 在Sxy上为一阶连续的偏导数，则对于求解的第二类曲面积分方程D(x，y，z)而言，如果该被积分方程能够满足第二类曲面积分的要求，则有如下表达式。

原计算表达式是对x，y 变量的积分，则通过公式法将原计算表达式中的z 变量，通过Σ 曲面方程表达式z = z(x，y)来替代，最终形成了对变量x，y 的二重积分，而变换后的整体结果的正负取值，则是由Σ 曲面的法向量与被替代变量的轴的夹角取值范围来确定，如果是锐角则取“+”，如果为钝角则取“－”。

上述表达式描述的是由于原始表达式只对x，y 变量求积分，那么通过对Σ 曲面方程的转换，将其变换成x，y 为z 的函数，并将被积分函数中的z 变量全部由x，y 变量替代，最终形成了只有对x，y 变量进行积分的二重积分，而转换后的整体结果，则要看Σ 曲面的法向量的方向与z 轴形成的夹角，通过看其夹角是锐角还是钝角来决定“+”或者“－”的取值。

例如，对于平面x +y +z = 2，Σ 曲面为该平面与x，y，z 坐标轴三个坐标平面截取的下部分的下侧，然后对方程I =进行求解。

首先要对Σ 曲面和被积分方程进行观察分析。很明显，无论x，y，z 轴如何变换，Σ 曲面以及被积分方程都不会变化，所以可以利用第二类曲面积分的第二个解题技巧，即利用曲面积分的轮换对称性，将被积分方程进行简化，在原计算表达式中，则原计算表达式可以转换成如下表达式:

然后，通过公式法，将被积分表达式中的z 变量通过x，y变量替代，Σ 曲面方程为x +y +z = 2，则有z = 2 －x －y，带入被积分方程中，则有y)2dxdy。然后对变换后的方程进行转换得到，I =，最终求得结果为－4 。

2．2 高斯定理算法

高斯定理又称为散度定理或高斯散度定理，是物理理论中用来表示在某个闭合曲面内的电荷分布与其产生电场的之间关系的表达式。

高斯定理定义为，假如空间内含有闭合区域Ω，且该区域的边界Ω 为分片光滑闭曲面，同时函数P(x，y，z)，Q(x，y，z)，R(x，y，z)，及其一阶偏导数在Ω 上为连续的，那么则有高斯公式为:

对于该题目的求解就可以利用高斯定理的方法来实现。首先要满足高斯定理的基本要求，对于一个闭合的曲面进行处理。那么假定有一平面Σ1为z = 0，与Σ 曲面构成一个完整封闭的区域Ω。在利用高斯定理求解前，可对被积分的函数进行公式法处理。由于，则有a2= x2+y2+ z2，由于a 为大于0 的任意常数，代入被积分函数可得，πa4= － πa3/2。

利用高斯定理来求解第二类曲面积分非常方便快捷，但是使用起来有几个关键点必须满足。首先要满足高斯定理的基本要求，即首先构成一个完整的封闭的区域空间，然后P，Q，R 函数在该空间上具有连续的一阶偏导数，而且求解的Σ 曲面为该封闭区域的外侧，所以对于不是封闭的区域首先要为其构建一个封闭的区域才能开始使用高斯定理求解，然后就可以利用高斯定理将被积分的函数通过高斯公式转变成x，y，z 变量的三重积分。如果Ω 空间区域内有某些奇点使得函数P，Q，R 在该空间上不能连续偏导，那就要先去除这些奇点，然后用高斯公式进行处理，最后再对这些奇点进行分析，最终实现对第二类曲面积分的计算。

2．3 利用第一类曲面积分求解法

利用第一类曲面积分来求解第二类曲面积分的方法就是考虑到二者之间的转换关系，只要能求出曲面的法向量，然后利用两类曲面积分之间存在的换算关系将被积分函数转换成第一类曲面积分表达式来求解。两类曲面积分表达式关系如下:

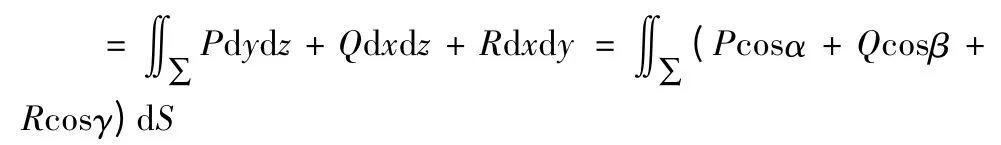
其中，cosα，cosβ，cosγ 是Σ 曲面在某个点出的法向量的方向余弦值。通过上述转换关系，即可对被积分的函数进行转换，最终将原计算表达式转换成对第一类由面积分的计算表达式，然后对其进行求解。

例如，一平面为x － y + z = 1，Σ 曲面为该平面在第四象限的上侧。则对于连续函数f(x，y，z)，计算如下曲面积分值I［2f(x，y，z)+3z］dxdy。由于该题目中并未给出f(x，y，z)函数的具体表达式，所以无法利用公式法和高斯定理将其进行转换，这时就可以考虑利用第一类和第二类曲面积分之间的关系进行求解。

对第二类曲面积分的求解，主要是利用解题技巧，将被积分的计算表达式进行简化处理，然后利用公式法、高斯定理或者利用两类曲面积分之间的换算关系来求解出曲面积分的最终值。

［1］杜美华，孙卫卫．第二类曲面积分的基本解题方法［J］．科技信息，2011，(5)．

［2］张文国，贾云涛．第二类曲面积分的讲授方法探讨与实践［J］．科技信息，2013，(7)．

［3］赵艳辉．第二型曲面积分的计算［J］．湖南科技学院学报，2013，(8)．

［4］孙庆虎．第二类曲面积分教学难点之突破［J］．合肥学院学报:自然科学版，2011，(1)．

［5］景慧丽，张辉．第二类曲面积分的计算方法［J］．高等数学研究，2011，(4)．