双线法与横摆角速度法联合的车辆稳定性判据

余卓平，冷 搏，2，熊 璐，2，冯 源

（1.同济大学汽车学院，上海201804；2.同济大学新能源汽车工程中心，上海201804；3.泛亚汽车技术中心有限公司，上海201201）

双线法与横摆角速度法联合的车辆稳定性判据

余卓平1，冷 搏1，2，熊 璐1，2，冯 源3

（1.同济大学汽车学院，上海201804；2.同济大学新能源汽车工程中心，上海201804；3.泛亚汽车技术中心有限公司，上海201201）

车辆稳定性判据决定了车辆稳定性控制系统的介入与退出时机，是车辆稳定性控制的基础.设计了一种基于相平面法的车辆稳定性判据，在传统双线法确定的稳定区域中引入横摆角速度法确定的稳定区域，设计联合车辆稳定性判据，协调对质心侧偏角和横摆角速度的控制，并获取稳定性判据的相应阈值变化的数据库，用于在控制过程中查表获得车辆的稳定区域边界.利用质心侧偏角和横摆角速度偏离函数表征控制变量偏离参考值的程度和车辆状态相对稳定区域边界的位置.极限工况下，当车辆状态超出稳定区域边界时，车辆稳定性控制应迅速介入，控制车辆状态回到稳定区域.

稳定性判据；质心侧偏角；横摆角速度；相平面法；稳定性控制

长期以来，汽车的安全性就是伴随汽车发展的主题之一.统计数据显示，车速在80～100km·h-1时，40%的交通事故与车辆侧滑失稳有关；当车速超过160km·h-1时，90%以上的事故是车辆侧滑失稳造成的［1］.因此，各大汽车公司相继研发了一系列车辆稳定性控制系统，其中最具代表性的是博世公司的电子稳定程序（electric stability program，ESP）［2］.美国联邦政府已于2011年将电子稳定性控制（electric stability control，ESC）系统纳入新的汽车安全标准［3］.

车辆稳定性判据为稳定性控制提供了控制目标和控制边界［4］，决定了其介入与退出时机，是车辆稳定性控制的基础.Shibahata等［5］提出βmethod，利用稳定横摆转矩及横摆转矩随前轮转角增加变化趋势表征车辆的稳定性，但其考虑的只是比较简单的稳态工况，也未提出明确的稳定界限.前轴侧偏角后轴侧偏角相图［6］以及质心侧偏角 横摆角速度相图［7］确定的稳定区域边界随车速变化的规律较复杂，不利于分析车速对车辆稳定区域的影响.考虑到车辆的极限转弯工况本质上是与侧偏运动相关的，Inagaki等［8］和Koibuchi等［9］提出并发展了利用质心侧偏角 质心侧偏角速度（ββ·）相平面图评价车辆的侧偏运动并分析车辆极限转弯工况下的稳定性的方法，并提出了“双线法”稳定性判据：利用相平面上2条平行通过鞍点的直线作为车辆稳定区域边界设计了稳定性控制策略.但其所确定的稳定区域是开放型的，这种区域中距离焦点较远的地方包含了较多的不稳定轨线.菱形法［10-11］对稳定区域的判定比双线法更准确，但其参数过多，并且难以确定.

双线法判据参数少，能够简单有效地判定不同工况下车辆的稳定性状态；但其只针对质心侧偏角的控制，不能对横摆角速度控制提供参考的阈值.本文在双线法的基础上引入横摆角速度阈值对双线法进行补充，协调对质心侧偏角和横摆角速度的控制，设计双线法与横摆角速度法联合的车辆稳定性判据并给出极限工况下车辆稳定性控制算法介入和退出的条件；在多种工况下的仿真和实车试验中验证判据的有效性.

1 非线性二自由度车辆模型

本文判据设计基于二自由度车辆单轨模型，如图1所示，图中点C表示车辆质心位置，点O表示车辆转向运动瞬心位置，αf与αr分别为前后轮侧偏角，β为车辆质心侧偏角，δf为前轮转向角，lf和lr分别为前后车轴到质心处的距离，γ为车辆横摆角速度，VCOG为车辆质心处速度，Fy，f和Fy，r分别表示前轴和后轴侧向力.

图1 二自由度单轨车辆模型Fig.1 Two degrees of freedom single track vehicle model

二自由度车辆模型的动力学方程如下：

式中：m为整车质量；V为车辆质心处速度VCOG的纵向分量；β·为车辆质心侧偏角速度；Jz为车辆横摆转动惯量.极限工况下，车辆进入非线性区，前后轴侧向力Fy，f，Fy，r可通过简化的“魔术公式”轮胎模型［12］计算，如下：

式中：μ为路面峰值附着系数；Fz，f和Fz，r分别为前轴和后轴垂向载荷；Bi，j（i＝1，2；j＝f，r）为轮胎特性拟合系数.αf，αr分别与β，γ，δf存在如下运动学关系：

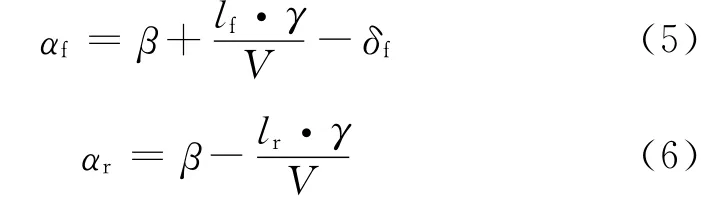
2 车辆稳定性判据

2.1 双线法确定的稳定性区域

根据文献［8］：双线法边界在横轴上的截距表征了双线法对稳态质心侧偏角的限值，是整个稳定区域边界的基点；它们分别为相图两侧的鞍点.双线法的边界斜率kβ可由式（7）计算，表征了对瞬态条件下质心侧偏角的限值，即不同质心侧偏角速度下的质心侧偏角限值；斜率绝对值越小，边界对瞬态条件下质心侧偏角的限制越强.

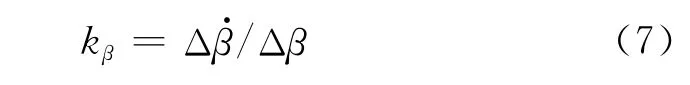
左侧（下）边界

右侧（上）边界

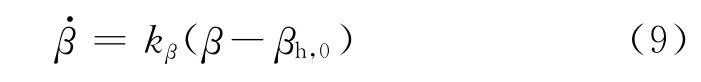
式中：βl，0和βh，0分别为双线法边界在横轴的左右截距.图2表示附着系数1.0、车速30m·s-1时不同转向角下的ββ·相图.

与图2a相比，图2b小转向角下收敛轨线的数量没有明显变化，稳定焦点向负方向（转向外侧，与侧向加速度方向相反）移动，轨线位置整体向右上方平移；两鞍点同时向转向内侧平移，转向侧的稳定区域变窄，另一侧的稳定区域变宽.继续增大前轮转角到5°时（图2c），两侧鞍点继续向非转向侧移动.正半轴鞍点内侧的轨线进一步增加，但受到负半轴鞍点移动的影响，一部分轨线运行偏离出稳定区域，最终未能收敛到焦点，车辆的右侧的收敛轨线数量反而减少，两鞍点之间出现了大片的不稳定区域，因此已不能再利用两鞍点来表示稳定边界.在图2c中以右侧为例，令最外侧收敛轨线与横轴交点为bc，最内侧发散轨线与横轴交点为bn，此时稳定边界在横轴的截距为

图2 附着系数1.0、纵向车速30m·s-1时的相图Fig.2 Phase plane whileμ＝1.0，V＝30m·s-1

取ib＝0.1以保证截距靠近稳定轨线一侧.当转向角增大时，收敛轨线全部消失，稳定区域也随之消失.

由对双线法稳定性判据分析可知：

（1）双线法判据参数少，能够简单有效地判定不同工况下车辆的稳定性状态；但其只针对质心侧偏角控制，不能对横摆角速度控制提供参考的阈值.

（2）双线法判据存在不足，只能判定质心侧偏角是否发散，车辆是否稳定；但对前轴侧滑导致车辆失去转向能力的工况无法判别，此时车辆的横摆角速度响应明显低于驾驶员的期望值，需要引入横摆角速度阈值对双线法进行补充.

2.2 横摆角速度法确定的稳定区域

参考横摆角速度γd可以设置为二自由度单轨车辆模型横摆角速度响应稳态值.

式中：l为轴距；K为车辆稳定性因数.

由式（1）～（4）计算质心侧偏角速度.

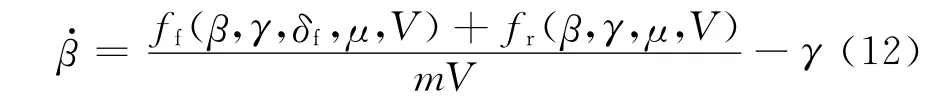
式（12）可以分解为减号前的非线性部分和减号后的线性部分.令γ＝γd，代入式（12）得

即，在保证车辆跟踪线性模型横摆角响应条件下，质心侧偏角速度变成了关于路面峰值附着系数、车速、前轮转角以及质心侧偏角的非线性函数，其中隐含了轮胎的非线性特性.在相图上，当确定了前3个变量后，质心侧偏角速度可以表示为仅关于质心侧偏角的函数

因此，根据式可以直接将满足线性横摆角速度约束的状态轨线直接画在相图上（图3）.

（1）在转向角为零时，轨线位于第2、第4象限，经过原点并与原点呈中心对称曲线呈现与侧偏角 轮胎力曲线类似的非线性特性.

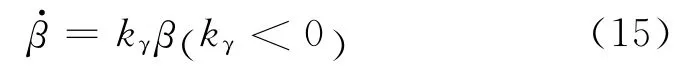
在线性范围内跟踪线性横摆角速度能对质心侧偏角有一定的抑制作用.在β 超出一定范围后，轨线的变化趋于平缓，甚至产生反向的变化.虽然轨线保持在稳定区域内，但此时继续跟踪线性横摆角速度，会导致迅速增加.

如图3所示，当线性横摆角速度约束的轨线（以下简称为γd轨线）移动到双线法边界与横轴交点时，γd轨线偏移量为最大.设Δγh和Δγl分别为边界轨线对应的横摆角速度相对于γd的上下偏移量，横摆角速度法确定的边界轨线应通过双线法与横轴的2个交点.边界对应的横摆角速度限值分别如下.

上限值

下限值

上限值γh对应的边界轨线在γd轨线下方，下限值γl对应的边界轨线在γd轨线上方.

图3 基于双线法与横摆角速度法联合的稳定性判据示意图Fig.3 Diagram of the joint criterion

2.3 双线法 横摆角速度法联合稳定性判据

横摆角速度法定义的稳定区域在β-β·上可以表示为一条与轮胎侧向力特性曲线形状相似的带状区域，该区域是一个沿着横轴方向无限延伸的开放区域；而根据2.1节中分析，双线法确定的稳定区域更接近一个沿着纵轴方向无限延伸的开放区域.如图3所示，2种判据联合起来互补构成一个封闭的稳定区域，双线法用于限制车辆的质心侧偏角，横摆角速度法用于控制车辆的横摆角速度跟踪参考值，形成基于双线法与横摆角速度法联合的稳定性判据.该判据可以同时提供横摆角速度和质心侧偏角的控制目标，协调车辆在极限工况下操纵性和稳定性.

高附路面上，当转向角为0°时（图4a），γd轨线位于2条边界之间，到2条边界的距离相等，此时上下限阈值绝对值大小相等，符号相反.施加2°的转向角后（图4b），γd轨线向下移动，上限阈值的绝对值减少，下限阈值的绝对值增加，表现为判据对过多转向的限制更加严格.进一步增加转向角到5°时（图4c），上限阈值对应的边界曲线已经与γd轨线重合，此时转向侧阈值为零.当转向角到7°时（图4d），γd轨线已经偏离出了2条横摆角速度轨线中间，处于不稳定轨线的范围内；此时上下限阈值均小于零，车辆的横摆角速度不再跟踪γd，而是被限制在一个更小的范围内以保持车辆的稳定性.

图4 附着系数1.0、纵向车速30m·s-1时的稳定区域Fig.4 Stable region whileμ＝1.0，V＝30m·s-1

与高附路面相比，低附路面上的横摆角速度法 稳定区域收缩.如图5所示，路面附着系数为0.3时，2°输入工况下，γd轨线已经偏离出稳定区域，与高附路面上的7°相比下降明显，说明车辆在低附路面上的机动性能明显降低.

图5 附着系数0.3、转向角2°、纵向车速30m·s-1时的稳定区域Fig.5 Stable regionμ＝0.3，δf＝2°，V＝30m·s-1

基于双线法与横摆角速度法联合的车辆稳定性判据的原理如图6所示.判据包括如下查表参数：kβ，βl，0，βh，0，γl，γh.

由式（8）和式（9）整理可得，已知kβ，βl，0和βh，0后，根据当前的质心侧偏角速度β·，可以得到动态条件下质心侧偏角的上下限值βh和βl.

图6 基于双线法与横摆角速度法联合的稳定性判据原理Fig.6 Principle of the joint stability criterion

横摆角速度上下限值γh与γl可由式（16）和式（17）计算得到.

双线法边界斜率可以由路面附着系数和车速2个变量查二维Map图确定（图7）.

图7 双线法边界斜率Map图Fig.7 Map of the boundary slope in sideslip angle method

稳态质心侧偏角限值、横摆角速度限值需要根据路面附着系数、车速以及转向角3个变量查三维Map图确定.研究发现，路面附着系数对稳定区域影响接近于比例缩放.因此可以先确定几个典型的路面附着系数，在一定的路面附着系数下研究车速和转向角变化对判据参数的影响，再对比不同路面附着系数时参数的Map图获得参数随路面附着系数的变化趋势.当路面附着系数为1.0时，4个参数的变化规律如图8所示.

3 车辆稳定性控制介入和退出条件

根据驾驶员对转向盘转角的输入选择线性二自由度模型稳态横摆角速度作为横摆角速度参考值γd，同时利用侧向加速度ay对参考值进行限制.

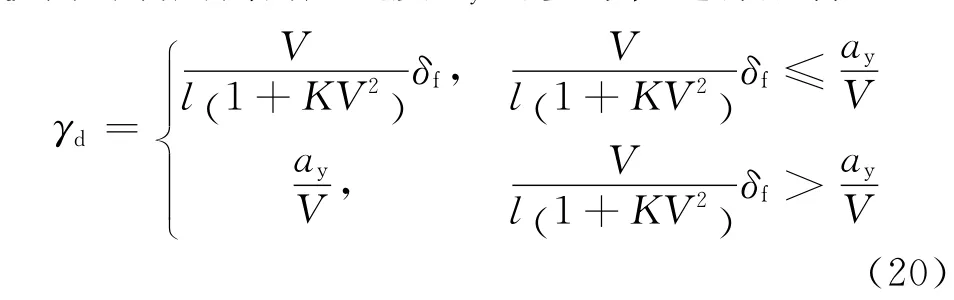
根据2.3节的分析，若选取稳态的质心侧偏角（相图焦点处的质心侧偏角）为质心侧偏角参考值βd会存在以下问题：一方面可能导致参考值与稳定区域边界的距离较小，进而降低稳定性裕度；另一方面也没有考虑动态条件下质心侧偏角速度对参考值的影响.因此，根据稳定性判据，设定参考的质心侧偏角为动态条件下质心侧偏角的上下限值的中位数.

质心侧偏角控制误差和横摆角速度误差分别为

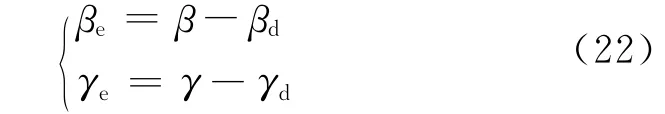
图8 路面附着系数为1.0时判据参数Map图Fig.8 Map of criterion parameters whileμ＝1.0

定义质心侧偏角偏离函数dβ和横摆角速度偏离函数dγ.

当满足max［dβ，dγ］＝1时，车辆状态已经达到或超出当前的稳定区域边界，此时车辆稳定性控制（vehicle stability control，VSC）算法的介入标志dVSC＝1，稳定性控制算法及时介入.

为了防止稳定性控制算法频繁地退出和介入，设置其退出条件与介入条件不等价：需要满足max［dβ，dγ］＜0.33，并且持续时间超过2s，才判定车辆状态恢复稳定，dVSC＝0，稳定性控制算法退出.

4 仿真分析

4.1 分布式驱动电动汽车

仿真车辆参数按照同济大学开发的分布式驱动电动汽车平台参数设置.平台车采用锂电池为动力源，4个车轮均装有可独立控制的轮毂电机以实现分布式驱动.车辆及轮毂电机参数如表1所示.

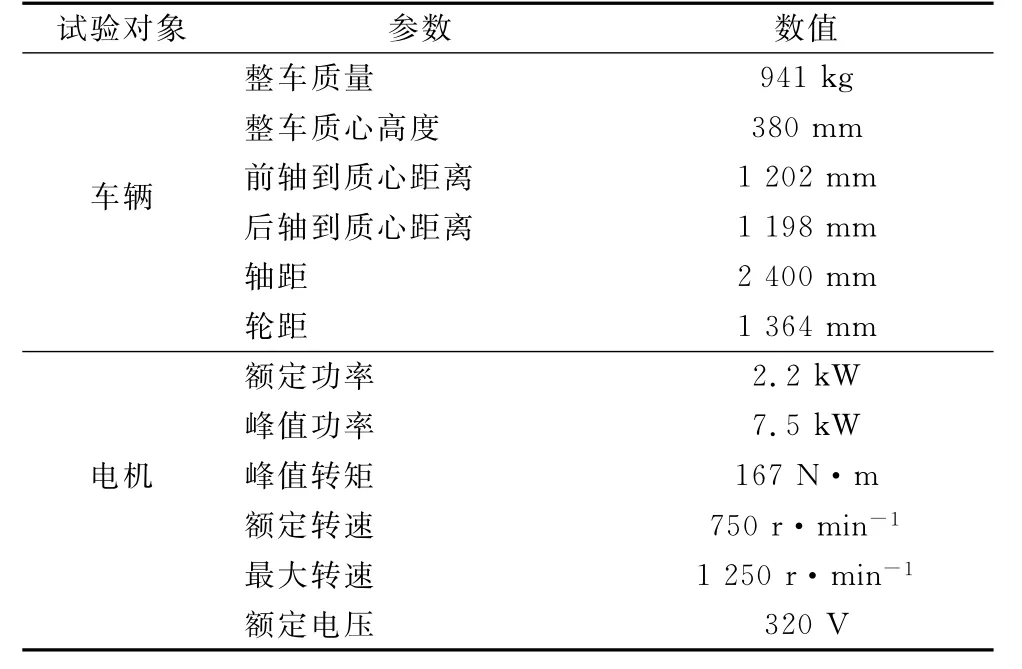
表1 试验车及电机参数Tab.1 Electric motor and test vehicle parameters

4.2 双移线工况仿真

利用CarSim软件和MATLAB／Simulink软件在国际标准ISO 3888 1：1999双移线工况［13］下进行联合仿真.根据表1中车辆参数设置通道宽度，选取路面附着系数为0.8，初始车速为30m·s-1.

车辆的动力学状态以及稳定性判据结果如图9所示.在驾驶员增加转向盘转角进行第1次变线的过程中，横摆角速度迅速增加并超过上限值，横摆角速度偏离函数迅速增加到1，dVSC＝1并一直保持到工况结束.

图9 车辆状态及稳定性判据结果Fig.9 Results of vehicle states and criterion

4.3 低附路面避障工况仿真

［14］中冰雪道路试验方法设置仿真工况.初始车速15m·s-1，路面附着系数0.3.车辆状态及判据结果如图10所示.

图10 车辆状态及稳定性判据结果Fig.10 Results of vehicle states and criterion

仿真过程中质心侧偏角和横摆角速度偏离函数迅速增加到1，判据准确判断车辆进入极限工况并将VSC介入标志置1.与2.3节分析相一致，低附路面上车辆稳定性裕度较低，稳定性判据给出的车辆稳定区域收缩.

5 实车试验分析

将本文的稳定性判据与车辆稳定性控制算法［15］结合，参考国际标准ISO 3888 2：2002［13］避障工况

进行实车试验，入口车速为65km·h-1，路面附着系数为0.8.图11为施加控制车辆和未施加控制车辆的控制效果对比.施加控制车辆的控制过程如图12所示.试验场地如图13所示.

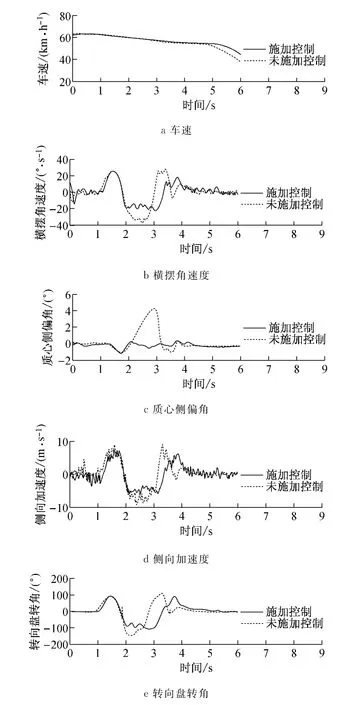
图11 避障工况试验控制效果对比Fig.11 Results of tests with and without control

图12 避障工况试验控制过程Fig.12 Control process of the tests

图13 避障工况试验场地布置Fig.13 Obstacle avoidance test field

未施加控制车辆的后轴在第1次变线后出现了明显侧滑，导致车辆质心侧偏角增大到接近5°，横摆角速度也产生了明显的超调；驾驶员发现车辆的甩尾倾向后提前将转向盘回正，质心侧偏角迅速减小，才没有发生车辆失稳.施加控制车辆能够以较小的质心侧偏角顺利地完成工况.在车辆稳定性控制介入后，车辆的横摆角速度能够较好地跟随参考值，横摆角速度偏离函数保持在0.5以下.质心侧偏角参考值一直保持与实际值异号，控制对质心侧偏角的抑制效果明显.避障工况驾驶员未进行任何加速踏板输入，控制过程中的车轮转矩基本保持左右对称，2～3s内的车轮转矩出现了较长时间的饱和，表明此时的控制需求最强；但随着变线机动完成后，驾驶员将转向盘回正到中间位置附近，控制需求逐渐降低；由于稳定性控制退出条件比介入条件更严格，到5.3s左右，过渡工况算法判定车辆已经足够稳定，车辆稳定控制退出.

6 结论

（1）基于传统双线法在ββ·相图上确定的稳定区域引入横摆角速度法确定的稳定区域，两者互补构成一个封闭的稳定区域，形成双线法与横摆角速度法联合的稳定性判据，协调对质心侧偏角和横摆角速度的控制；在考虑路面附着系数、车速以及转向角变化的条件下获取稳定性判据的相应阈值变化的数据库，用于在控制过程中查表获得车辆的稳定区域边界.

（2）设计了质心侧偏角和横摆角速度偏离函数以表征控制变量偏离参考值的程度和车辆状态相对稳定区域边界的位置.极限工况下，当车辆状态超出稳定区域边界时，车辆稳定性控制迅速介入，控制车辆状态回到稳定区域.

（3）通过CarSim软件和MATLAB／Simulink软件联合仿真以及实车试验验证了设计的车辆稳定性判据的有效性和实用性.

参考文献：

［1］ Frampton R，Thomas P.Electronic stability control：Review of research and regulations［M］.Britain：Vehicle Safety Research Center Longhborough University，2007.

［2］ Van Zanten A T.Bosch ESP systems：5 years of experience［C］／／SAE Automotive Dynamics ＆Stability Conference.Troy：［s.n.］，2000：2000-01-1633.

［3］ US Department of Transportation，National Highway Traffic Safety Administration.RIN：2127 AJ77 Electronic stability control systems［S］.Washington D C：Federal Motor Vehicle Safety Standard，2006.

［4］ Van Zanten A T.Evolution of electronic control systems for improving the vehicle dynamic behavior［C］／／Proceedings of the 6th International Symposium on Advanced Vehicle Control.Hiroshima：［s.l.］，2002：1-9.

［5］ Shibahata T，Shimada K，Tomari T.Improvement of vehicle maneuverability by direct yaw moment control［J］.Vehicle System Dynamics，1993，22：465.

［6］ Pacejka H B.Non-linearities in road vehicle dynamics［J］.Vehicle System Dynamics，1986，15（5）：237.

［7］ Ko Y，Lee J.Estimation of the stability region of a vehicle in plane motion using a topological approach［J］.International Journal of Vehicle Design，2002，30（3）：181.

［8］ Inagaki S，Kushiro I，Yamamoto M.Analysis on vehicle stability in critical cornering using phase-plane method［J］.JSAE Review，1995，16（2）：187.

［9］ Koibuchi K，Yamamoto M，Fukada Y，et al.Vehicle stability control in limit cornering by active brake［C］／／SAE Internaitonal Congress ＆Exposition.Detroit：［s.n.］，1996：960487.

［10］ Von Vietinghoff A，Lu H，Kiencke U.Detection of critical driving situations using phase plane method for vehicle lateral dynamics control by rear wheel steering［C］／／Proceedings of the 17th World Congress，The International Federation of Automatic Control.Seoul：［s.l.］，2008：5694-5699.

［11］ Chung T，Yi K.Design and evaluation of side slip angle-based vehicle stability control scheme on a virtual test track［J］.Control Systems Technology，2006，14（2）：224.

［12］ Pacejka H B.Tire and vehicle dynamics［M］.3rd ed.Oxford：Butterworth-Heinemann，2012.

［13］ British Standard Institution.ISO 3888，Passenger cars-test track for a severe lane-change manoeuvre［S］.London：British Standard Institution，2002.

［14］ 中国国家标准化管理委员会.ICS42.040.40轻型汽车电子稳定性控制系统性能要求及试验方法（征求意见稿）［S］.北京：中国标准出版社，2012.Standardization Administration of the People’s Republic of China.ICS 42.040.40 Performance requirements and testing methods for electronic stability control system（ESC）for light vehicles（exposure draft）［S］.Beijing：Standards Press of China，2012.

［15］ XIONG Lu，YU Zhuoping，WANG Yang，et al.Vehicle dynamics control of four in-wheel motor drive electric vehicle using gain scheduling based on tyre cornering stiffness estimation［J］.Vehicle System Dynamics，50（6）：831.

Vehicle Sideslip Angle and Yaw Rate Joint Criterion for Vehicle Stability Control

YU Zhuoping1，LENG Bo1，2，XIONG Lu1，2，FENG Yuan3
（1.School of Automotive Studies，Tongji University，Shanghai 201804，China；2.Clean Energy Automotive Engineering Center，Tongji University，Shanghai 201804，China；3.Pan Asia Technical Automotive Center Co.，Ltd.，Shanghai 201201，China）

Vehicle stability criterion is the basis of vehicle stability controls and decides the control intervention time and exit time.A phase-plane method based criterion combing the sideslip angle method and the yaw rate method is proposed，which can coordinate the control of both vehicle sideslip angle and yaw rate.By means of phase-plane method the data bases of the stable region thresholds are obtained，which contributes to establishing look-up tables of the thresholds for real-time control.Deviation functions of the sideslip angle and the yaw rate are designed to indicate the deviation between vehicle actual states and the reference states.Meanwhile，relative positions of the vehicle states and the stable region boundaries are also described by the deviation functions.When the vehicle states are beyond the stable region，the vehicle stability control should intervene timely to make the vehicle back to stable state.

stability criterion；vehicle sideslip angle；yaw rate；phase-plane method；stabilitycontrol

U46

A

0253-374X（2015）12-1841-09

10.11908／j.issn.0253-374x.2015.12.012

2014 11 17

国家“九七三”重点基础研究发展计划（2011CB711200）；国家自然科学基金（51475333）

余卓平（1960—），男，教授，博士生导师，工学博士，主要研究方向为汽车系统动力学及控制.E-mail：yuzhuoping@tongji.edu.cn

熊 璐（1978—），男，副教授，博士生导师，工学博士，主要研究方向为汽车系统动力学与控制.E-mail：xiong_lu@tongji.edu.cn