基于时域卷积的瞬态响应计算方法及精度分析

曹建华

（中国人民解放军92853部队，辽宁 兴城125106）

数字信号处理虽然发展得比较充分，但是瞬态冲击响应计算依然是备受关注的课题。而工程问题中都会有以下时域响应计算问题:对于一个H系统，在时域作用力f（t）下的时域响应，计算的收敛性依然是难题。例如:瞬态冲击声辐射计算，这类问题就存在计算收敛的问题。因此常常通过频域计算，以及转换到时域的求解方法。文献［1］讨论了频域 DFT 以及IDFT［2－3］的计算步骤:即对输入信号作DFT变换，与系统传递函数在频域作乘法，然后对结果IDFT变换得到瞬态响应。本文将讨论另外一种频域计算方法，即对传递函数的IDFT变换结果，与输入信号进行时域卷积获得瞬态响应，讨论在保证计算精度条件下节省计算时间的方法。

1 卷积计算和DFT→IDFT分析的对等性原理推导

假设传递函数的迪拉克冲击响应为h（t）（即对传递函数IDFT的结果），瞬态响应采用DFT和IDFT技术有:

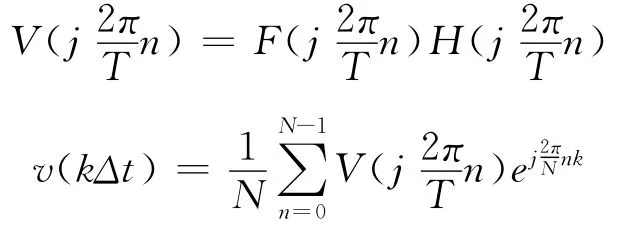
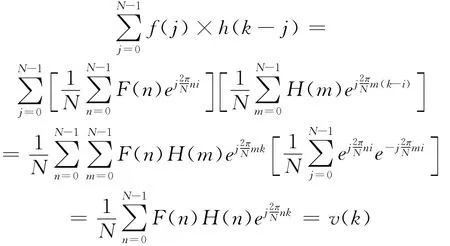
所以最终有

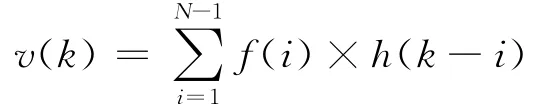
2 频域计算误差原因和卷积计算提高精度的可能方法

对于频域计算存在两个误差:频域截断，时域混叠。

2.1 时域混叠

数字DFT、IDFT是基于周期信号的理论，认为每一个小片段是一个周期，某个周期的响应可以看成信号前一系列周期输入的输出叠加和（图1）。

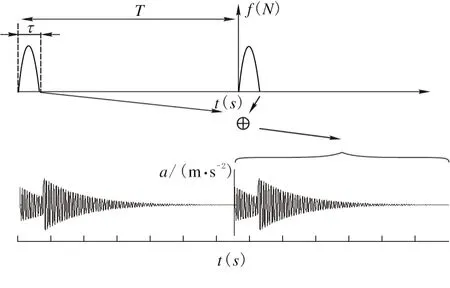
图1 响应为一系列冲击叠加

为了减小计算误差，尽管冲击时间很短，为了减小叠加效应，单个周期的计算时间T应该足够长，以使时域叠加效果尽量减弱。由于频率分辨率Δf＝1

T，因此要求在频域计算时频率分辨率足够大。

2.2 频域截断

另外一个问题是频域截断，即要求计算频率足够高。考虑矩形信号

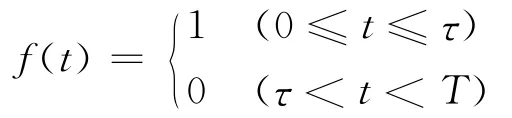
采样见图2，假设采样频率为fs。

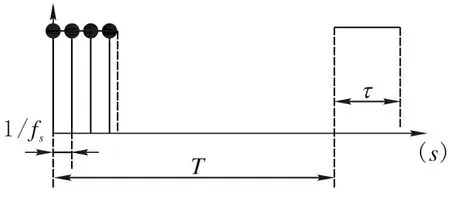
图2 以fs采样频率对矩形采样

对DFT变换只取该频率级数的有限项，当展开采用更高的采样率时，细线为更高采样频率展开信号。尽管在采样点复合较好，在更高采样点与原信号不复合，这就是采样混叠造成的误差（图3）。

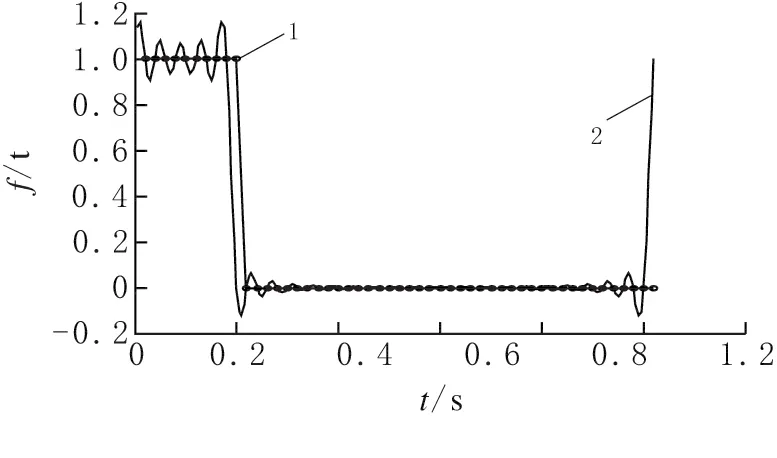
图3 采样混叠的影响

2.3 卷积计算误差

DFT→IDFT瞬态响应计算步骤是对输入信号作DFT变换，与系统传递函数在频域作乘法，然后对结果IDFT变换得到瞬态响应，流程见图4。

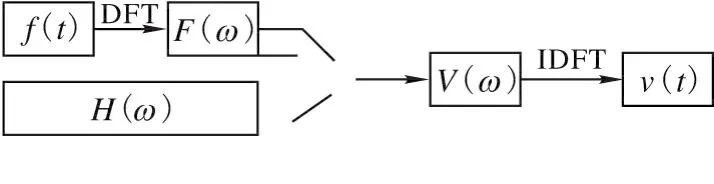
图4 DFT→IDFT计算方法流程

采用卷积的计算为对传递函数的IDFT变换结果与输入信号进行时域卷积获得瞬态响应，框图见图5。

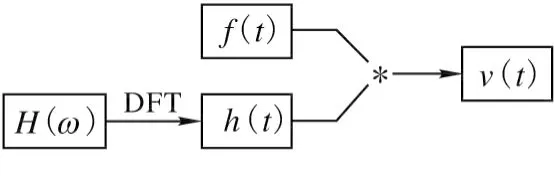
图5 卷积方法计算流程

卷积计算存在同样的计算误差问题，从H（"）获得h（t）计算量比较大的工作，在通过有限个频率点的H（"）获得h（t）时，提高精度的可能方法在H（"）插值获得更高的采样频率，从而期望减小时域混叠；而h（t）后在时域插值就是为了在f（t）采样率比较高时，充分利用f（t）的信息以减小误差，计算步骤见图6。

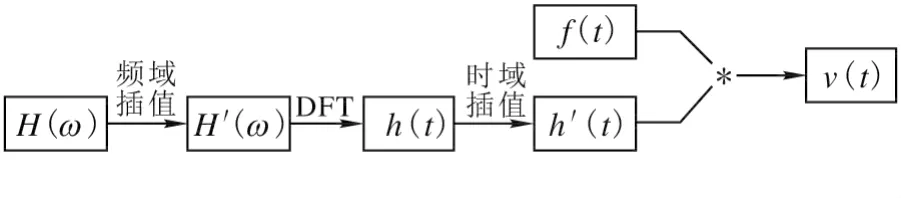
图6 采用插值法的瞬态计算方法

3 算例和验证

图7所示单自由度系统振动方程为

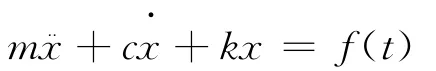
其中m为质量，c为粘性阻尼系数，k为弹簧刚度，f为冲击力。有振动传递函数［4］

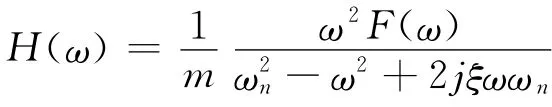
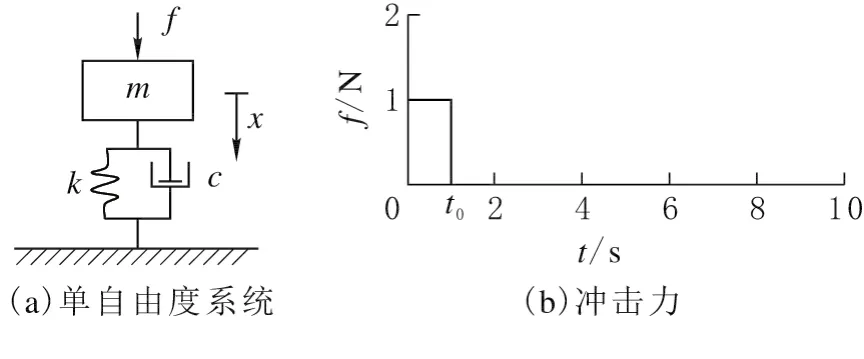
图7 单自由度系统冲击计算

3.1 时域标准解

矩形冲击信号解析响应为:

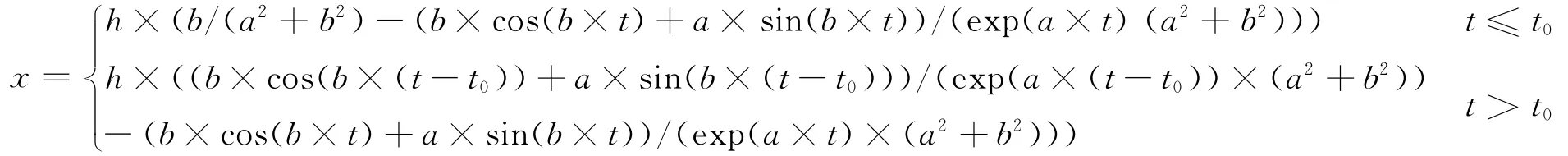
取m＝1，c＝1，k＝100，冲击时长t0＝0.5，采用DFT-IDFT计算时，数字计算频率取一阶系统共振频率的10倍，时间长度取

输入信号频谱见图8a，传递函数频谱见图8b。

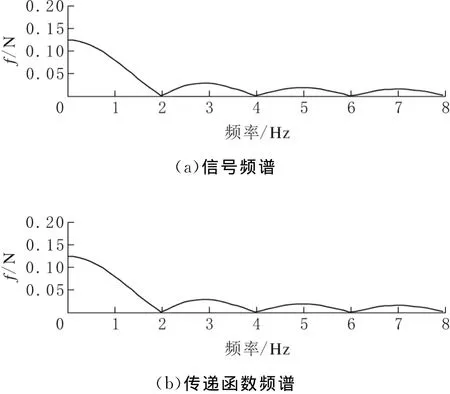
图8 信号和传递函数频谱

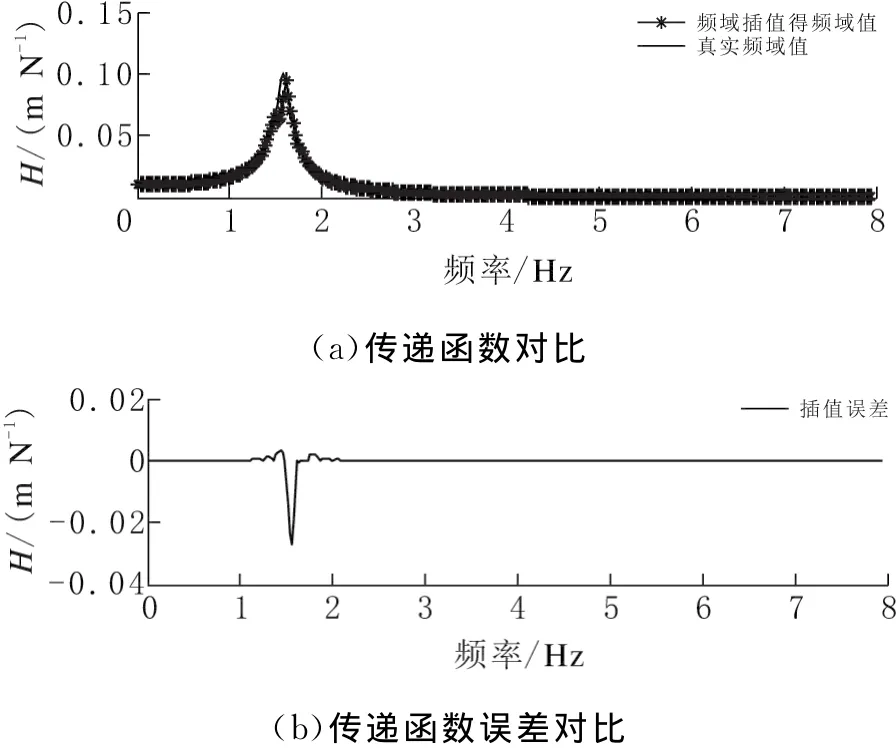
图10 传递函数进行频域插值误差分析

时域插值可以获得较好的结果，误差对比见图11。

3.2 传递函数频域和时域插值对h（t）计算精度的影响

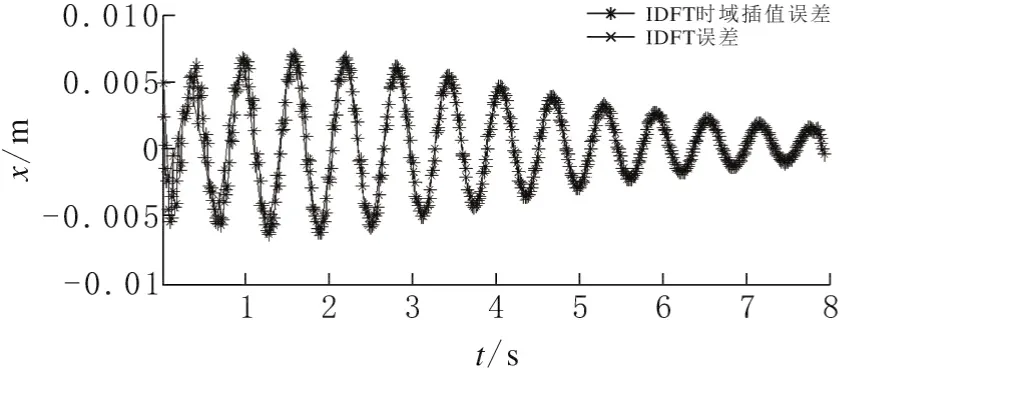
图11 IDFT时域插值与解析解误差对比

对传递函数进行频域插值然后IDFT计算与真实解析解对比见图9。频域插值计算精度不高，主要原因是频域插值时传递函数存在较大误差，见图10。

3.3 整体计算精度对比

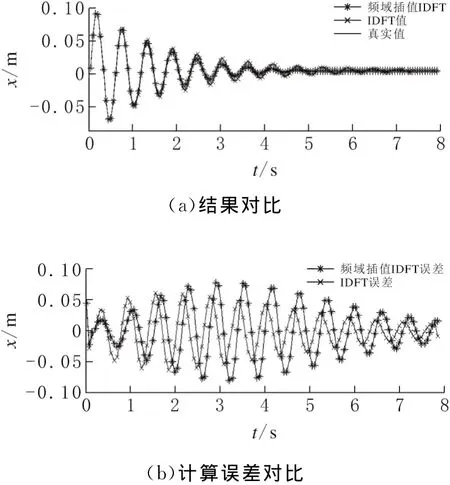
图9 传递函数频域插值后IDFT计算与h（t）解析解对比

图12 采用DFT→IDFT方法和卷积结果及真实值对比，采样频率同样，卷积与DFT→IDFT计算精度完全相同。

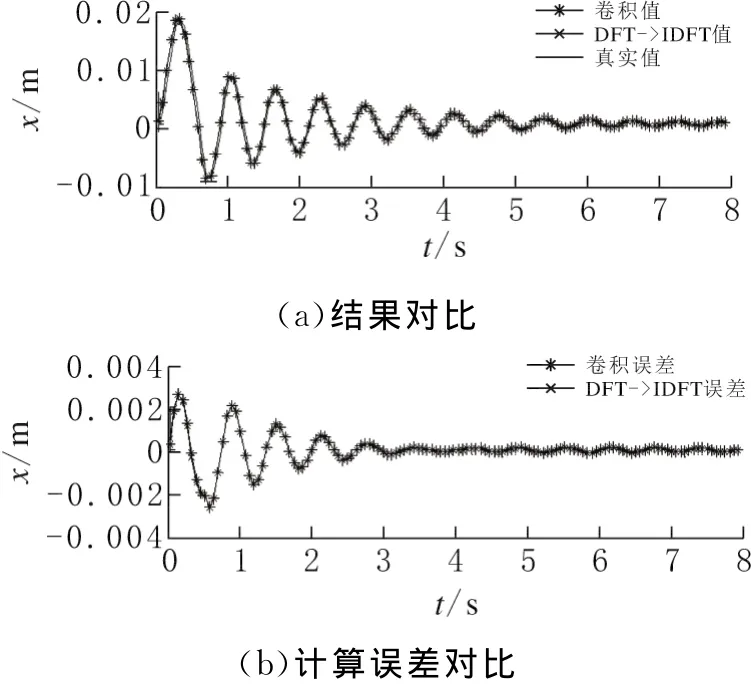
图12 采用DFT→IDFT方法和卷积和真实值对比

图13 是频域时域插值卷积和DFT→IDFT误差对比，频域时域都插值卷积结果在后半部分逊于DFT→IDFT计算结果。

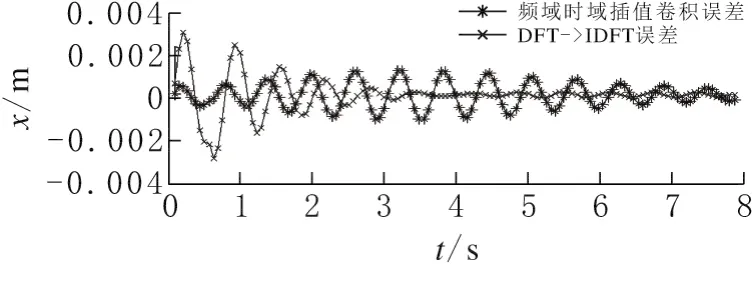
图13 频域时域插值卷积和DFT→IDFT计算误差对比

图14 是时域都插值卷积和DFT→IDFT计算误差对比，可发现时域插值光时域插值除了可以改善初始段计算精度外，相对于都插值，尾段计算精度有所提高，其根本原因是通过H（"）获得H′（"）时插值精度无法得到保证，因此损坏了计算精度；由h（t）获得h′（t）时，输入信号可以获得更高采样精度输入，因此总的计算精度得到了提高。

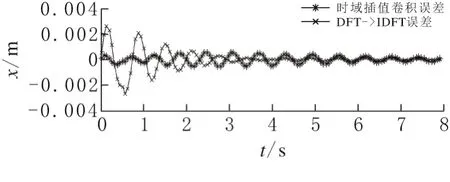
图14 时域插值卷积和DFT→IDFT计算误差对比

4 结论

本文研究了采用卷积计算瞬态响应的方法，讨论了频域插值和时域插值在有限计算量时提高计算精度的可能性，表明输入信号采样频率高于传递函数计算截止频率时，对传递函数进行时域插值可以有效提高计算精度。本文研究结果可以用于一些纯时域计算不收敛的问题，如:瞬态边界元分析等。

［1］ Cao Jianhua，Wang Yingjian，Wu Xianjun.Discussion on transient response analysis based on DSP［C］.IEEE:Proceeding of the 2nd International Conference on Mechanic Automation and Control Engineering.Inner Mongolia，China:IEEE，2011:4 905-4 908，

［2］ 文顿P R.数据处理和误差分析［M］.北京:知识出版社，1986:190-200.

［3］ 丁玉美，高西全，彭学愚.数字信号处理［M］.西安:西安电子科大出版社，1997:50-80.

［4］ 闻邦椿.机械振动理论及应用［M］.北京:高等教育出版社，2009:1-30.