圆形地下连续墙围护结构体型特征响应分析

2015-01-18胡威旺

湖北工业大学学报 2015年5期

胡伟，胡威旺

（湖北工业大学土木工程与建筑学院，湖北武汉430068）

对于圆形地下连续墙围护结构的研究，文献［1］分别用平面弹性地基梁法、三维弹性地基板法及三维连续介质有限元法对工程实例进行计算和模拟，得出了圆形地下连续墙应该采用三维弹性地基板法的结论。文献［2］以平面弹性地基梁法为基础，将拱效应等效成密集的水平支撑，效仿三维空间对墙体的影响。文献［3］在三维空间内构建了一个既满足双调和方程又满足边界条件的新应力函数，对厚壁圆筒在柱面上受双曲余弦分布压力、端面受正压力总和为常力的情况给出了解析解。可见，大多关于地下圆形连续墙的研究都趋向于分析方法的研究，而关于墙体随其体型特征变化的研究较少。本文从文献［2］和文献［3］关于应力和位移的解析解出发，计算分析了影响圆形地下连续墙的外在因素及其对应的内力和位移变化情况，分析结果显示，墙体厚度、基坑开挖深度及墙体半径的变化对于墙体径向应力影响极小，墙体厚度及基坑深度对墙体环向应力及径向位移具有较大影响，墙体半径对于墙体环向应力及径向位移的影响呈线性趋势。

1 墙体内力及位移解析解

平面弹性地基梁法将围护结构等效成竖向抗弯构件进行分析，从而忽略了圆形地下连续墙的空间拱效应。为考虑地下连续墙空间拱效应的影响，本文根据空间轴对称应力问题的双调和方程［3］求得墙体应力的解析解，设圆形地下连续墙半径为r，内径为2a，外径为2b（图1），墙顶土体受荷载q作用。由弹性力学［4］和双调和方程［3］可推导出墙体内力和位移的解析解。

图1 圆形地下连续墙示意图

式中pz是关于截面计算高度z的线性函数:pz＝p1），t＝b－a，为墙体厚度，E为圆形墙体弹性模量，ν为泊松比。当z＝l－d时，即计算点位于墙顶时，σr、σθ及μr均达到极小值；当z＝0，即计算点位于基坑底部时，σr、σθ及μr均达到极大值。

从计算结果可以看出，墙体环向应力σθ在数值上较径向应力σr大，二者差值为。这说明，圆形地下连续墙的拱效应特性使得墙体的环向抗压性能得到充分发挥，墙体混凝土强度等级由σθ控制。

2 体型变量计算分析

由公式（1）及计算结果可以看到，控制圆形地下连续墙体型特征主要有3个参量:墙厚t，圆形墙体半径r及基坑开挖深度s，为方便作对应分析，本文设置3个工况。工况1:墙体厚度t为变量，其余参量不变；工况2:基坑开挖深度s为变量，其余参量不变；工况3:墙体厚度r为变量，其余参量不变。以此3个工况，分别分析墙体内力和位移变化。

2.1 工况1

假定墙体厚度t为变量，基坑开挖深度l－d、圆形墙体内半径a、计算点半径r（为计算方便，假定r为定值）及嵌入土体深度d均为衡量，由公式（1）有

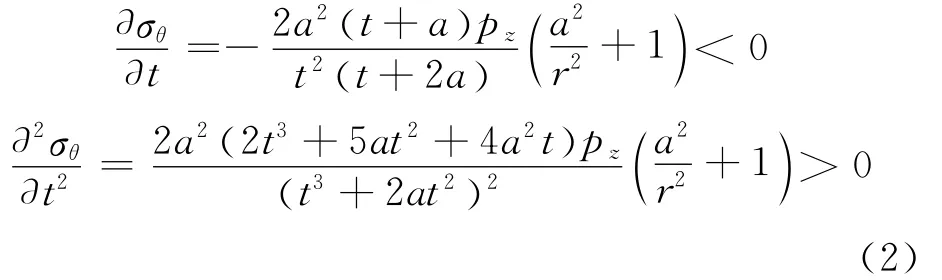
同样μr也可以得到类似（2）中σθ的表达式，这里不再累述。由于r＝a＋，在工程实际中，相对于a来说，t很小，r→a，故→0，这说明墙厚t的变化对于径向应力σr几乎无影响。而σθ及μr随着t增大而逐渐加速减小。

2.2 工况2

假定基坑开挖深度s为变量，a、b、t及计算点高度z均为定值。令l－d＝s，则l－z－d＝s－z，随基坑s增大，s－z处土压力则不变。而

因式（2）中应力及位移与pz为线性关系，故而pz的变化规律能代表应力及位移的变化。据式（4）分析，在基坑开挖取土的过程中，随着基坑深度增大，应力及位移与 s 为反正切关系，即（σr，σθ，μr）＝C1arctan（f（s））＋C2，C1及C2为常数。可见，深度s增大，σr、σθ及μr均呈放缓方式增大。

2.3 工况3

假定墙体半径r为变量，厚度t不变，a＝rt/2，b＝r＋t/2，r＞＞t，其他条件不变。由式（2）有

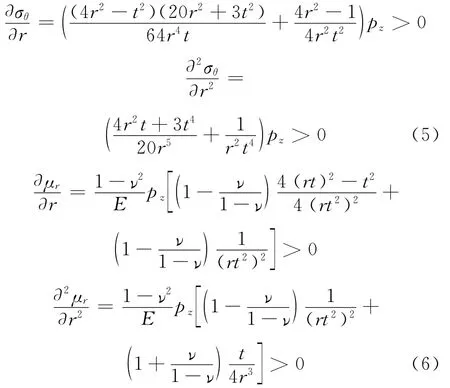
以上3个工况的分析结果显示，t、r及s对于σr的影响均较小，而对于σθ及μr有较大影响；工况1显示，t的增大，能有效减小μr和σθ，说明增大墙体厚度能有效提高墙体环向承载力，控制墙体位移；工况2和3显示，随着s和r增大，σθ及μr快速增大，其中s对σθ及μr呈反正切函数变化，r对σθ及μr呈线性函数变化。

3 算例

某悬索桥两侧锚定基坑采取地下连续墙作为基坑围护形式，设计内径为39.6m，外径为40.4m，厚度为0.8m，混凝土等级C30，墙体嵌入土层深度为8.5m，基坑深度40m，为方便研究，本文设基坑土开挖分10个阶段进行，假定每个阶段下挖深度为4m。土层分布情况见表1。

表1 土层分布

对应上小节计算分析步骤，本算例建立2组对比性计算模型，每组5个模型，共10个模型。模型分组如下:第一组:内径39.6m保持不变，基坑深度及嵌入深度均不变，墙体厚度分别选取t＝0.4 m、0.6m、0.8m、1.0m 及1.2m，建立5个对比模型。第二组:墙体厚度保持不变，基坑深度及嵌入深度不变，墙体中心线直径分别选取r＝36m、38m、40m、42m，及44m建立5个对比模型。

因每组模型中设有10个基坑开挖阶段，每个模型模拟过程中已自动完成基坑开挖深度变化的模拟。因而无需再建立基坑深度变化模型，可任选一个模型，本文取第一个模型。上小节提到，计算点位于基底时，σθ及μr均达到极大值，为减小计算量，完成对比分析过程，本算例选择基底（即s＝40m）为计算点进行计算和分析对比。计算数据整理后，结果见图2～图7。

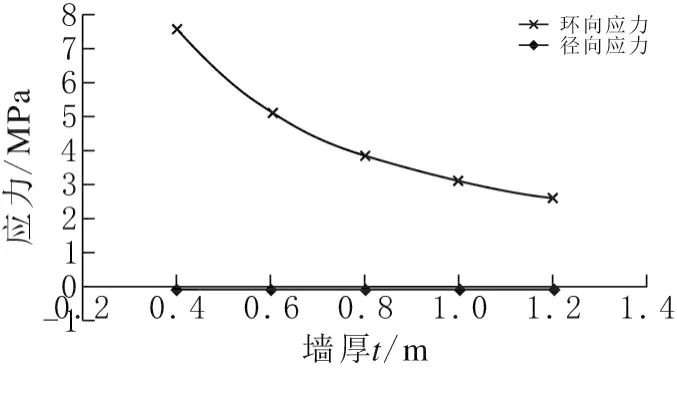
图2 墙体应力随墙厚（t）变化曲线

图3 墙体位移随墙厚（t）变化曲线

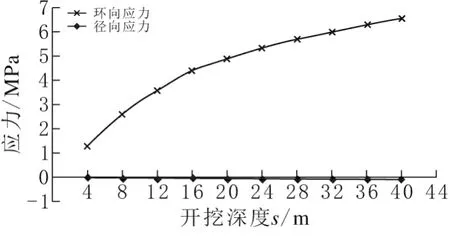
图4 墙体应力随开挖深度（s）变化曲线

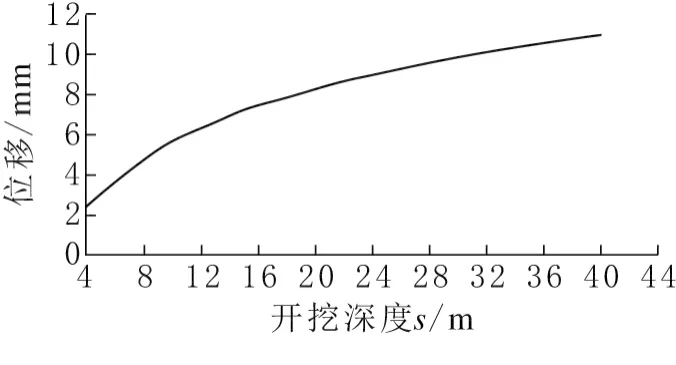
图5 墙体位移随开挖深度（s）变化曲线

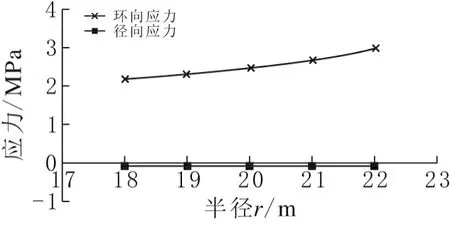
图6 墙体应力随半径（r）变化曲线

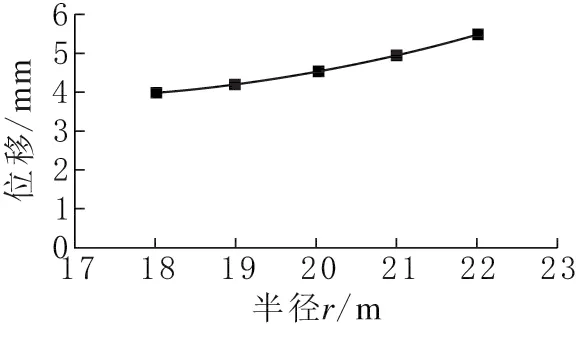
图7 墙体位移随半径（r）变化曲线

图2 及图3显示，t、r及s对于σr的影响可以忽略不计。t＝1.2m与t＝0.4m基底环向应力比约为0.35，位移比约为0.3。图4及图5显示，σθ及μr随s的增大而大幅增大，只是增大趋势逐渐趋于平缓。图6及图7显示，σθ及μr的大小与r基本趋近于线性变化，从数值上看，r＝22m与r＝18m基底应力比约为1.3，位移比约为1.4，可见r对σθ及μr的影响程度有限。