自由抛落式救生艇落水冲击响应及可靠性分析

苏石川，戴成龙，史 俊，张 文，张 力，高 强，张顺东

(1.江苏科技大学能源与动力工程学院，江苏镇江212003)

(2.镇江四洋柴油机制造有限公司，江苏镇江212003)

自由抛落式救生艇落水冲击响应及可靠性分析

苏石川1，戴成龙1，史 俊2，张 文1，张 力1，高 强1，张顺东1

(1.江苏科技大学能源与动力工程学院，江苏镇江212003)

(2.镇江四洋柴油机制造有限公司，江苏镇江212003)

自由抛落式救生艇入水过程开始时，艇体与水面接触瞬间将产生巨大的冲击力脉冲，这一脉冲力有可能造成救生艇内部结构失效.在救生艇入水过程中，存在固、液、气三相的耦合，其过程较为复杂.文中以某救生艇为研究对象，主机配置为380 J，应用有限元分析方法对其入水冲击过程进行数值仿真，分析自由抛落后冲击载荷对艇体的冲击响应.最终得出:最大变形发生在入水时间t=0.35 s，即救生艇开始向水面浮升的时，最大变形量为34.3 mm;最大应力发生在t=0.035 s，为95 MPa，应力变化在材料承受范围内，艇身不会被破坏.

艇体变形;冲击载荷;自由抛落式救生艇

自由抛落式救生艇以入水速度快、快速动作、避免近体危险等特点，至今已广泛应用在船舶、海洋平台等海上设备.针对救生艇结构安全性和可靠性方面的研究，目前国内外已取得了可观的进步和收获，主要是通过实验测量或有限元分析软件对艇身结构和强度进行分析［1-2］.

在救生艇入水过程开始时，艇体与水面接触瞬间将产生巨大的冲击力脉冲，很有可能造成救生艇内部结构失效.因此，文中通过对救生艇入水冲击过程进行数值仿真模拟，分析其冲击过程中艇体变形及应力变化，为救生艇的可靠性设计提供参考.

1 满载救生艇基本参数

文中以某380J船用自由抛落式救生艇为研究对象，该自抛艇的主要技术参数如表1.

表1 救生艇基本参数Table 1 Basic parameters of the lifeboat

取救生艇抛落角度为30°，入水角度为53°，下落高度为20 m，为便于计算，假定自抛艇是规则物体，底面积近似为S=6.7 m×2.55 m=17.1 m2，满载总质量m=6 475 kg.

根据文献［3］中的计算方法，经计算得救生艇入水时竖直方向分速度V2H=18.4 m/s.

当救生艇完全浸入水面，即入水深度为3.2 m时，垂向速度VH=11.6 m/s.

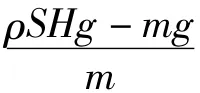
当速度减为零时，所用入水时间t=0.15 s，此时间段也是作用在救生艇上的最大受力时间.该过程入水深度h=0.91 m，则救生艇总入水深度H= 4.11 m［3-4］，该过程入水位移为0.91 m，则救生艇总入水深度H=4.11 m，ρ为水密度，取ρ=103kg/m3.

2 模型建立与处理

2.1 模型建立与网格划分

根据已有相关图纸和数据，进行艇体三维建模.再用HyperMesh有限元划分软件对模型进行网格划分.艇体网格划分模型如图1.随后将画好网格的救生艇模型导入有限元计算分析软件Patran中.

在救生艇入水冲击仿真过程中需对流体(空气、水)部分建立欧拉区域，采用8节点六面体网格单元进行划分.由于艇体十分复杂，在不影响反映艇体变形整体情况的条件下，为节省计算量，采用节点数量较少，救生艇及流体的节点数和单元数见表2.

补水泵站主厂房抗浮稳定及基底应力均满足规范要求，井筒及其内部板梁的配筋满足强度要求。连通洞结构设计符合规范和已有工程经验，结构的稳定满足规范要求，配筋满足强度要求。

图1 网格划分Fig.1 Meshing map

表2 节点及单元数Table 2 Number of nodes and elements

最后调整救生艇的入水角度，完成最终的有限元网格分析模型，将其导入有限元分析前处理软件中.

文中所研究的救生艇用聚酯纤维玻璃钢的一般性能常数如表3.

表3 聚酯纤维玻璃钢一般性能Table 3 General performance of polyester fiber glass steel

救生艇玻璃钢材料采用Von Mises屈服模型，屈服应力取290 MPa［5］.

流体域主要包括空气域和水域，流体域欧拉单元初始条件的定义内容主要为比内能和密度.流体域中，空气和水的状态方程参数值如表4.表中:ρ为密度;γ为空气比热比;E为单位质量的内能;a1为水的体积弹性模量.

表4 流体域状态方程参数Table 4 State parameters of fluid field equation

救生艇入水冲击仿真计算的初始条件主要包括救生艇结构与流体间的流-固耦合边界、救生艇初速度、欧拉单元初始状态等条件.在仿真过程主要模拟救生艇抛落过程的第4阶段，即救生艇在接触水面到法向加速度达到最大时刻的冲击过程.由上文计算可知，救生艇抛落的水平倾斜角为35°，接触水面时刻的倾斜角度为53°，抛落高度为20 m.

随后对艇体模型进行速度加载，并定义流-固耦合边界.

为提高计算效率，文中只分析救生艇开始接触水面到加速度达到最大时的冲击过程.初始，救生艇最低端距水面距离为0.05 m，分析计算时间定义为0.36 s，初始时间步长为1×e-7s.定义初始条件的完整有限元计算分析模型如图2所示［6-8］.艇身并且应力分布逐渐趋于均匀;由图d)可以看出:冲击过程结束后，由于能量不能及时传递到艇体外界，应力变化存在一定的残余响应.当艇体将要浮出水面时，即当t=0.35 s时，冲击残余应力已均匀分布于整个艇体，只在救生艇的拐角结构等处出现局部应力集中的情况.

图2 救生艇入水初始边界条件Fig.2 Initial diving boundary conditions of lifeboat

3 艇体形变及应力分析

3.1 等效应力分析

救生艇以53°入水角度跌入水中，救生艇与水面接触的瞬间，艇首的等效应力迅速增大，并将冲击能量以应变、应力形式传递到艇体及动力装置.冲击过程不同时刻t的艇体应力变化如图3.

由图a)可以看出:当冲击开始时，艇首与水面正面冲击，冲击部位的应力值迅速增大.随着救生艇着水区域的增大，艇首的最大应力值也随之迅速增大，并且冲击能量以应力、应变的形式，传递到整个艇身;由图b)可以看出:当冲击时间t=0.058 s时，艇首出现比较明显的应力集中情况并达到最大值;由图c)可以看出:当t=0.1 s时，救生艇大部分艇身已浸入水中，冲击载荷已由艇首传递到整个

图3 艇体不同时刻应力分布云图Fig.3 Hull stress distribution nephogram of different time

图4 救生艇最大应力变化曲线Fig.4 Maximum stress change curve of lifeboat

冲击过程中，最大应力的大小及位置随着冲击时刻的变化而不断变化.其冲击过程中，救生艇最大应力随时间的变化情况如图4.从图3，4可以看到，最大应力σ分布范围主要集中在艇首与水面接触的初始区域内，在t=0.035 s时应力分布出现的最大值为95 MPa，发生在救生艇首部与水面初始接触位置.由救生艇玻璃钢材料特性可知，此时的应力小于玻璃钢的最大安全应力120 MPa，所以认为救生艇受冲击后不会发生破坏状况.

3.2 艇体变形分析

图5为救生艇在不同冲击时刻艇体的变形云图，从救生艇的变形图中分析可知，最大变形发生在t=0.35 s时，即救生艇开始向水面浮升的时刻，最大位移为33.3 mm，发生在救生艇尾部.不同冲击时刻救生艇出现不同的变形响应.由图a)可以看出:冲击过程开始瞬间，艇首最先与水面接触，冲击能量瞬间集中于救生艇首部，造成了如图a)所示的变形响应.随后冲击响应沿艇首迅速向艇体传递，所以艇首的冲击变形首先迅速增大，然后稍有减小并趋于稳定.救生艇入水初始过程中，首部相当于受到水的约束作用，致使救生艇尾部受到巨大惯性力及扭转力矩作用，扭转力矩使救生艇尾部产生弯曲变形，救生艇的弯曲变形要远大于冲击载荷所造成的冲击变形.当救生艇接近入水深度最低点时，救生艇已完全浸入水中，此时扭转力矩作用消失，尾部变形达到最大值，如图b).

图5 艇体应变响应云图Fig.5 Nephogram of hull strain response

分别取救生艇艇首、艇侧、艇尾及顶部观的测点，对救生艇入水冲击过程中的应力变化情况进行分析，其观测点节点编号分别为node 81、node 5 310、node 3 876和node 6 181.图6为各个观测点冲击过程中的位移时程曲线.从图中可以看出:艇首观测点(node 81)最先与水面接触，所以位移D迅速增大并首先达到最大值，之后随着时间t的变化先减小而后略有增加并趋于稳定值.这种现象发生的主要原因是因为玻璃钢具有较高的韧性.距离冲击位置较远的艇侧观测点(node 5 310)与顶部观测点(node 6 181)由于没有与水面直接撞击，所以冲击变形响应相对较为缓慢.救生艇艇尾观测点(node 3 876)的冲击位移响应随时间变化较为平缓.不同观测点的位移响应各不相同，这主要是因为救生艇在入水过程中，与救生艇结构、入水姿态以及冲击能量在救生艇内部的传递和转化过程有关.

图6 不同观测点位移变化曲线Fig.6 Observation points maximum displacement change curve

4 结论

1)艇体在冲击过程开始时，最大应力迅速增大，并在t=0.035 s时应力分布出现最大值为95 MPa，艇首观测点变形量于t=0.35 s时达到最大值为33.3 mm，之后随着时间的变化先减小而后略有增加并趋于稳定值.

2)艇侧观测点与顶部观测点冲击变形响应相对较为缓慢.救生艇艇尾观测点的冲击位置响应随时间变化较为平缓.

References)

［1］Re A S，Veitch B.A comparison of three types of evacuation system［J］.Transactions-society of Naval Architects and Marine Engineers，2007(115):119-139.

［2］Bradley Elliott.Computer simulation of a freefall evacuation system in a range of initial conditions［R］.Canada:NRC Research Press，2003.

［3］ 黄春平，陆军，秦嘉岷.自由降落救生艇试验过程探讨［J］.造船技术，2012(3):37-40.Huang Chunping，Lu Jun，Qin Jiamin.Research on free-fall lifeboats test process［J］.Marine Technology，2012(3):37-40.(in Chinese)

［4］ 贺玉英，杨金芳.船舶自抛救生艇［J］.船舶，1996 (5):30-33.

［5］黄燕玲，郭强波，廖文，等.小型玻璃钢开敞艇结构强度分析［J］.船海工程，2013，42(1):21-22.Huang Yanling，Guo Qiangbo，Liao Wen，et al.Direct calculation of structural strength of a small FRP yacht［J］.Ship＆Ocean Engineering，2013，42(1): 21-22.(in Chinese)

［6］Von K T.The impact of seaplane floats during landing［R］.Washington USA:National Advisory Committee for Aeronautics，NACA TN 321，1929:1-8.

［7］Wagner V H.Phenomena associated with impacts and sliding on liquid surfaces［J］.Z Angew Math Mech，1932(12):193-215.

［8］Shiffman M，Spencer D C.The force of impact on a cone striking a water surface［J］.Commun Pure Appl Mech，1951(4):379-417.

［9］苏石川，王宪淼，孙江，等.自由抛落式救生艇推进系统落水冲击响应计算分析［J］.中国造船，2013，54(3):114-122. Su Shichuan，Wang Xianmiao，Sun Jiang，et al.Simulation and analysis of response of propulsion system of free-fall lifeboat to water entry impact［J］.Shipbuilding of China，2013，54(3):114-122.(in Chinese)

［10］ 苏石川，张未军，王永，等.外载荷作用下船舶推进系统非线性动力学分析［J］.中国造船，2012，53 (1):79-87.Su Shichuan，Zhang Weijun，Wang Yong，et al.Calculation and analysis of non-linear dynamics of propulsion system with external load［J］.Shipbuilding of China，2012，53(1):79-87.(in Chinese)

［11］Det Norske Veritas.Design of free fall lifeboats［S］.Oslo Norway:Det Norske Veritas，2010.

［12］Karim M M，Iqbal K S，Khondoker M R H，et al.Influence of falling height on the behavior of skid launching free-fall lifeboat in regular waves［J］.Journal of Applied Fluid Mechanics，2011，4(1):77-88.

［13］ 宋长福.民机机身机构入水冲击问题数值仿真研究［D］.上海:上海交通大学，2011.

［14］ 王军.鱼雷入水冲击动力学仿真研究［D］.云南昆明:昆明理工大学，2010.

(责任编辑:贡洪殿)

Analysis of water entry impact response of free fall lifeboats and its reliability

Su Shichuan1，Dai Chenglong1，Shi Jun2，Zhang Wen1，Zhang Li1，Gao Qiang1，Zhang Shundong1

(1.School of Energy and Power Engineering，Jiangsu University of Science and Technology，Zhenjiang Jiansu 212003，China) (2.Zhenjiang Siyang Diesel Engine Manufacturing Co.Ltd.，Zhenjiang Jiangsu 212003，China)

When the lifeboat falls into water，the impact pulse created is so great that the structure of the boat may be destroyed.In the process，there exists the coupling of gas，liquid and solid phases，so the process may be very complex to be analyzed.A lifeboat whose main engine is 380 J is used in this study as the research object.The finite element analysis method is used to simulate the lifeboat water impact process.Finally，the conclusion is made that when t=0.35 s，the biggest displacement is 34.3 mm.When t=0.035 s，the biggest stress is 95 MPa.The biggest stress is within the material stress range and the body of the boat will not be destroyed.

ship deformation;impact load;free fall lifeboat

U662.3

A

1673-4807(2015)06-0511-05

10.3969/j.issn.1673-4807.2015.06.001

2015-06-08

资金项目:镇江市科技支撑基金资助项目(GY2014047)

苏石川(1963—)，男，教授，研究方向为动力装置性能优化及可靠性.E-mail:15606103818@163.com

苏石川，戴成龙，史俊，等.自由抛落式救生艇落水冲击响应及可靠性分析［J］.江苏科技大学学报(自然科学版)，2015，29(6):511-515.