弱相容映射几个新的公共不动点定理

张树义， 赵美娜， 刘冬红

(渤海大学 数理学院，辽宁 锦州121013)

1 引言与预备知识

1982 年Sessa S［1］定义了弱交换映射，1986 年Jungck G［2-3］引入了比弱交换更广泛的相容映射的概念并在完备度量空间中研究这类映射的不动点存在性。李高明［4］给出一个新型不动点定理推广了一些文献中的结果;谷峰等［5］将文献［4］推广为4 个映射的弱交换的情形;陈仕洲［6-7］在完备度量空间中研究相容和弱相容映射对的公共不动点存在性。张石生［8］、ZHANG Y S 等［9］、郑晓迪［10］和张树义等［11-12］先后给出几类Φ 型不动点定理。文中利用非单调不减的压缩尺度函数Φ(t)，进一步研究与文献［9-12］完全不同的另一类Φ 型弱相容映射对的公共不动点存在和唯一性，所得结果改进和推广了现有文献［1-8］中的结果。

全文设(X，d)是完备度量空间，S，T，A，B 为X上自映射。

定义1［1］称A 和S 是弱交换的，若∀x ∈X，有d(ASx，SAx)≤d(Ax，Sx)。

定义2［2］称A 和S 是相容的，若对任意{xn}⊆X，使，有

定义3［3］称A 和S 是弱相容的，若对u ∈X，有Au =Su，则ASu = SAu。

易知，A 和S 可交换⇒A 和S 弱可交换⇒A 和S相容⇒A 和S 弱相容，反之不然［3］。

定义4［9］设Φ(t)是定义在R+= ［0，∞)上的非负实值函数，且，当t ＞0 时，称Φ(t)为压缩尺度函数。

注1 若非负实值函数Φ(t)在R+上单调不减且Φ(t)＜t，∀t ＞0，则Φ(t)是压缩尺度函数。引理1［9］设Φ(t)是压缩尺度函数，则

1)对任意t ＞0，Φ(t)＜t;

2)设{an}n≥0，{bn}n≥0是两个非负实数列，∀n ≥0，an＞0，并且使an+1≤Φ(an)+ bn对所有n ≥0 成立，如果，则

引理2［8］设{yn}是X 中满足d(yn，yn+1)=0 的序列，若{yn}不是X 中的Cauchy 列，则必有∃ε0＞0 和正整数列{mi}和{ni}，使得①mi＞ni+1，ni→∞(i →∞)。②d(ymi，yni)≥ε0;d(ymi－1，yni)＜ε0，i =1，2，…。

2 主要结果

定理1 设A 和S 弱相容，B 和T 弱相容且AX ⊆TX，BX ⊆SX 或AX ⊆TX，BX ⊆SX，ψ:X × X →［0，∞)是对称有界函数，ψ(x，x)= 0，∀x ∈X 且对每一变量的任一固定值，ψ(·，·)对另一变量是连续的，如果∀x，y ∈X 以下条件成立:

1)ψ(Ax，By)≤β·ψ(Sx，Ty)，β ∈［0，1);

2)d(Ax，By)≤Φ{max(d(Sx，Ty)，d(Sx，Ax)，d(Ty，By)［d(Sx，By)+ d(Ty，Ax)］)}+ ψ(Ax，By)，其中，Φ 为右连续的压缩尺度函数。则S，T，A，B 在X 中存在唯一公共不动点。

证 由Φ 右连续性和引理1 可知，Φ(0)= 0。任取x0∈X，不妨设AX ⊆TX，BX ⊆SX，则∃x1∈X，使Sx1= Bx0。同理，∃x2∈X，使Tx2= Ax1。一般地，∃x2n－1∈X，使Sx2n－1= Bx2n－2= y2n－2，∃x2n∈X，使Tx2n= Ax2n－1= y2n－1n = 1，2，3，…。ψ(y2n－1，y2n)=ψ(Ax2n－1，Bx2n) ≤ βψ(Sx2n－1，Tx2n) =βψ(y2n－2，y2n－1)。 同 理 可 证，ψ(y2n，y2n+1) ≤βψ(y2n－1，y2n)，从而∀n ≥1，有

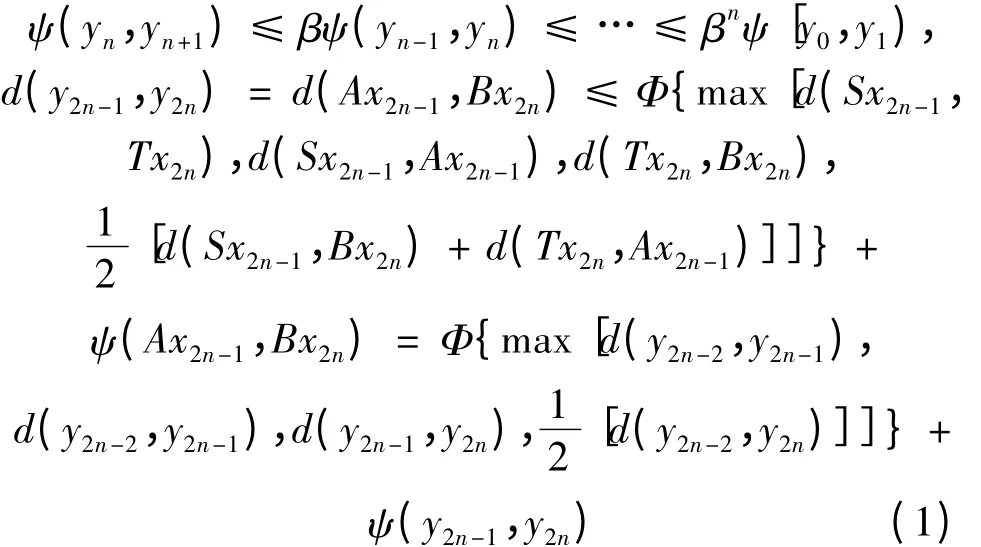
若d(y2n－1，y2n)＞d(y2n－2，y2n－1)，则由式(1)得

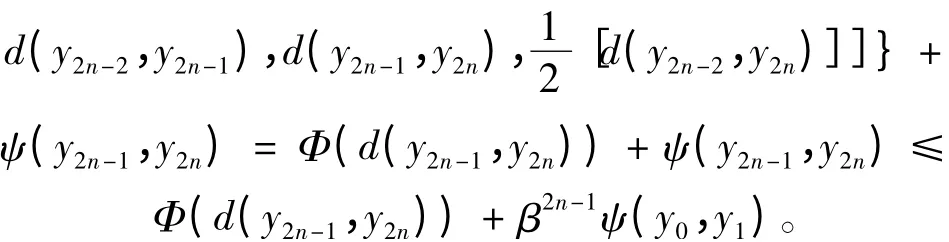
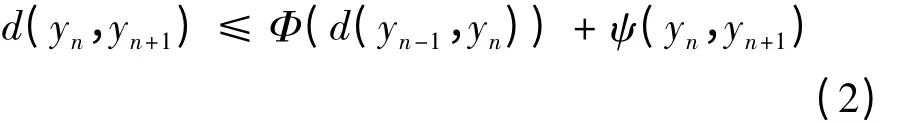
若存在正整数k，使yk= yk+1，则∀i ≥0，d(yk+i，yk+1+i)= 0。事实上，当i = 0 时显然成立。当i = 1时，由ψ(yk+1，yk+2)≤βψ(yk，yk+1)= 0，得d(yk+1，yk+2)≤Φ(d(yk，yk+1))+ ψ(yk+1，yk+2)= Φ(d(yk，yk+1))= Φ(0)= 0，假设i = m 成立，则i = m +1，有 ψ(yk+m+1，yk+m，+2) ≤ βψ(yk+m，yk+m+1) ≤βm+1ψ(yk，yk+1)= 0，由式(2)得d(yk+m+1，yk+m+2)≤Φ(d(yk+m，yk+m+1))+ f(yk+m+1，yk+m+2)= Φ(d(yk+m，yk+m+1))= Φ(0)= 0。

故由归纳法∀i ≥0，有d(yk+i，yk+1+i)= 0。于是∀n ≥k，有d(yn，yn+1)= 0，从而(yn，yn+1)=0。因此，以下可设yn≠yn+1，∀n ≥1，从而d(yn，yn+1)＞0。由于，故ψ(yn，yn+1)＜∞，于是由式(2)及引理1 知

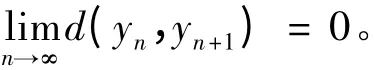
下证{yn}是X 中的一个Cauchy 列。若不然，由引理2，必∃ε0＞0 和正整数列{mi}，{ni}，使得:

①mi＞ni+1，ni→∞，i →∞;②d(ymi，yni)≥ε0，d(ymi－1，yni)＜ε0i = 1，2，…

令di= d(ymi，yni)，则有

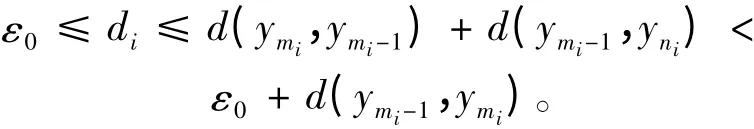
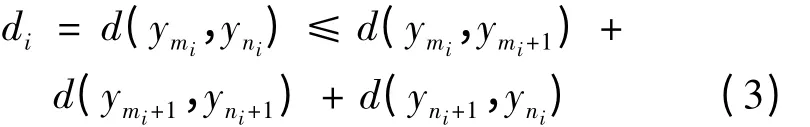
对式(3)右端第2 项分4 种情进行讨论:

情形1 当mi为偶数、ni为奇数时，由条件①有ψ(ymi+1，yni+1)≤βni+1ψ(ymi－ni，y0)→0(i →∞)，由条件②有d(ymi+1，yni+1)= d(Axmi+1，Bxni+1)≤Φ(max{d(Sxmi+1，Txni+1)，d(Sxmi+1，Axmi+1)，

因为

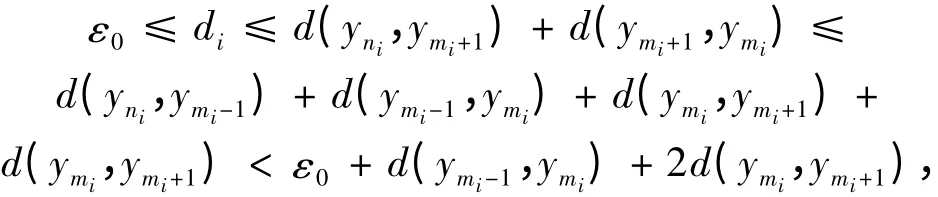
所以

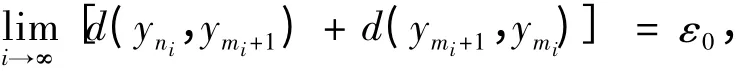
从而

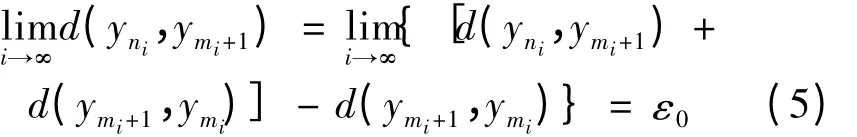
又

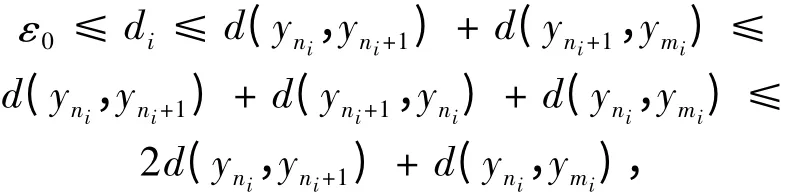
因此

于是有

将式(4)代入式(3)式，并令i →∞，使用式(5)和式(6)式，得，矛盾。

情形2 当mi为偶数、ni为偶数时，由条件①有

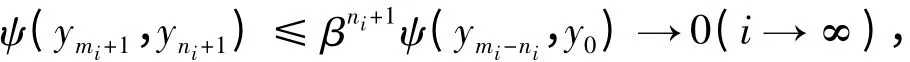
由条件②有

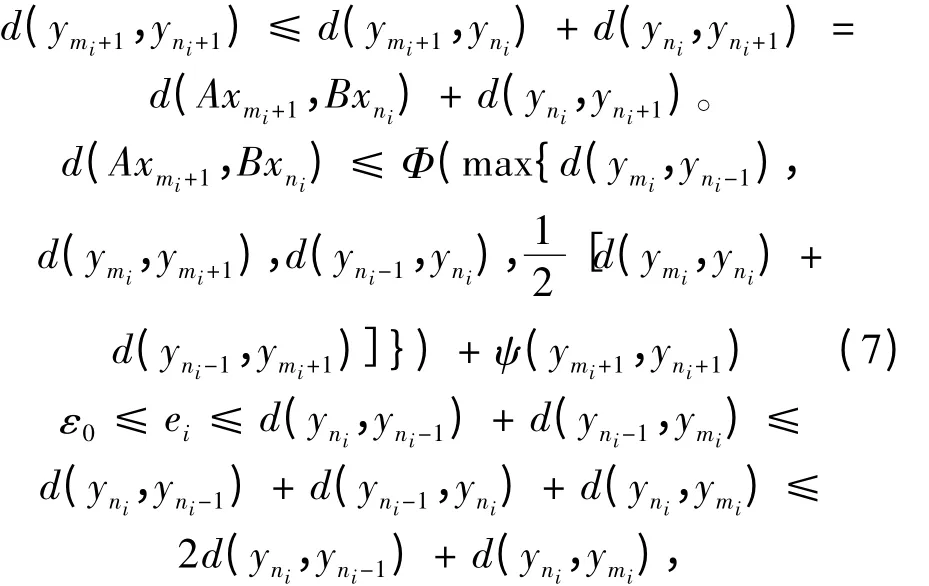
因此

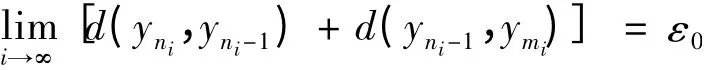
于是有

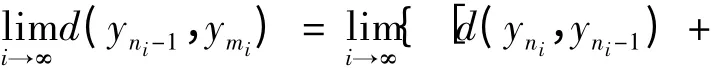
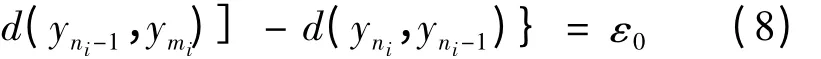
又

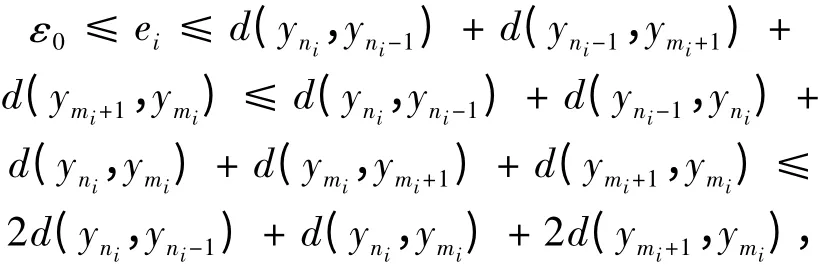
因此

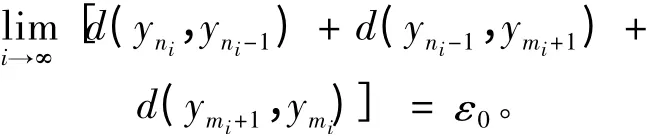
于是有

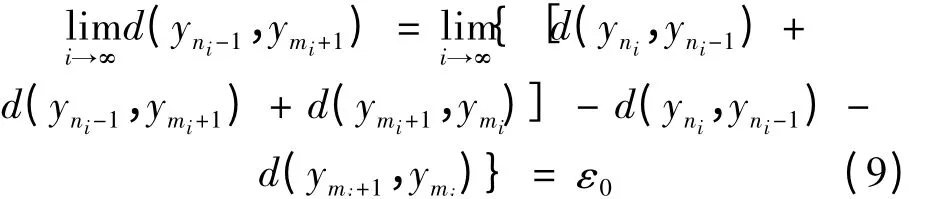
将式(7)代入式(3)式并令i →∞，使用式(8)和式(9)式，得矛盾结果

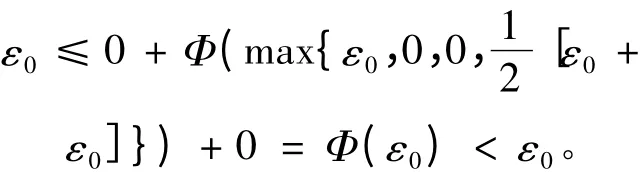
同理可证，mi，ni同为奇数;mi为奇数，ni为偶数的情形也产生同样的矛盾。因此{yn}是X 中的一个Cauchy 列。由于X 完备，故∃z ∈X，使得yn=z。显 然，{yn}的 子 列{Tx2n} = {Ax2n－1}和{Sx2n+1}={Bx2n}都收敛于z。由于⊆SX，因此z ∈BX，从而∃u ∈X，使得Su = z。由ψ(Au，Bx2n)≤βψ(Su，Tx2n)，

令n →∞，得ψ(Au，z)= 0，

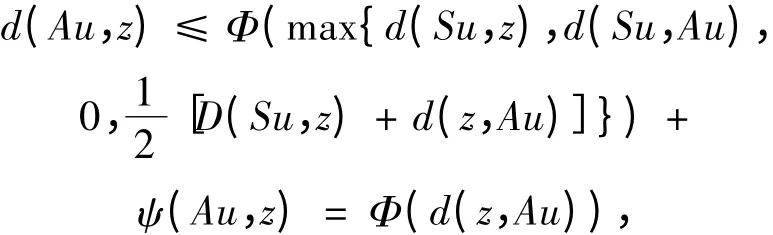
从而推出Au = z = Su。注意A 和S 弱相容，得SAu =ASu。即Az = Sz。

由

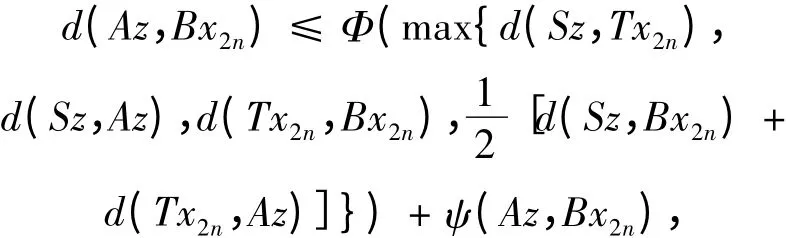
令n →∞，得ψ(Az，z = 0)，

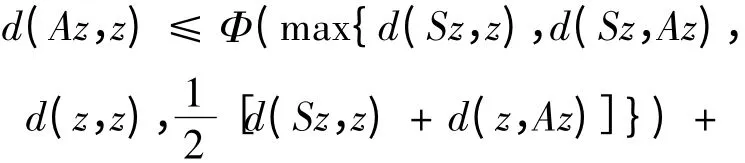
故Az = z，从而Sz = z。由AX ⊆TX，知∃v ∈X，使得Tv = Az = z，由ψ(Az，Bv)≤βψ(Sz，Tv)= 0，得

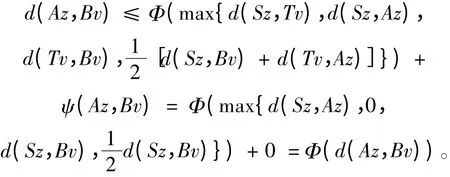
故Bv = Az = Tv。因B 和T 弱相容，得BTv = TBv，即BAz = TAz，故Bz = Tz。再由

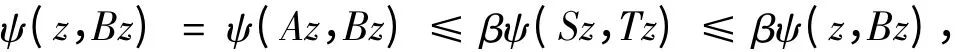
注意到β ∈［0，1)，得ψ(z，Bz)= 0，

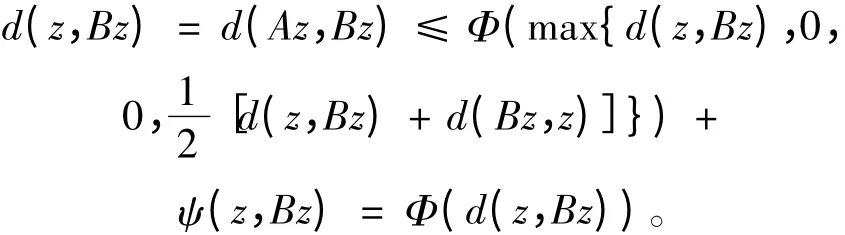
故Bz = z。综上，Az = Bz = Sz = Tz = z。最后，设z*∈X 也是A，B，T，S 的公共不动点，则由

因为0 ≤β ＜1，所以ψ(z*，z)= 0，

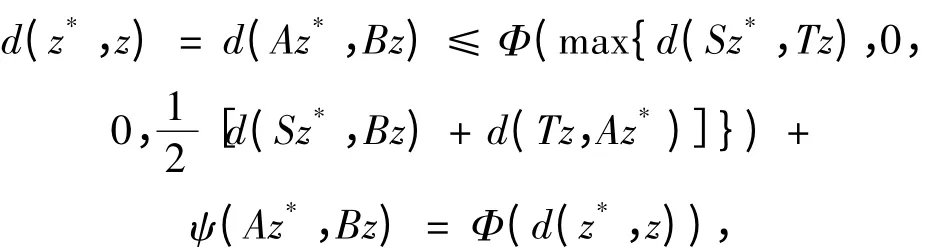
得d(z*，z)= 0，即z*= z。因此，A，B，T，S 在X 中存在唯一公共不动点。证毕。

注2 关于Φ-映象的不动点问题的研究，以往都是在Φ 满足单调不减的条件下进行讨论的［5-7］，而对Φ 不满足单调不减条件的Φ-映象的不动点问题的讨论并不多见。文中利用非单调不减的压缩尺度函数Φ(t)，研究了更广泛的Φ-ψ 型弱相容映射对的公共不动点存在性和唯一性，因此文中结果适用范围更加广泛。

注3 在定理1 中取Φ(t)在R+上单调不减，ψ(x，y)≡0 时即得文献［7］中的定理1;取Φ(t)在R+上单调不减，ψ(x，y)≡0，B = I(恒等映象)且A 和S，T 分别可交换时，便得文献［8］中的定理3.5.1。注4 在定理1 中取Φ(t)= αt(0 ≤α ＜1)，S =T =I(恒等映象)即得文献［4］中的定理1;取Φ(t)=αt(0 ≤α ＜1)且A 和S 弱交换，B 和T 弱交换，便得文献［5］中的定理2.10.1 ;取Φ(t)=αt(0 ≤α ＜1)且A 和S，B 和T 是两对相容映象，即得文献［6］中的定理1 (不过文中研究Φ-ψ 型映射(定理1 条件2))的不动点时，增加了ψ(x，y)的有界性)。

定理2 设A，B，Ti(i ∈∧，指标集∧的势≥2)都是X 上的自映射，⊆TiX，BX ⊆TiX 或(AX ⊆TiX，BX ⊆TiX)，i ∈∧，A，B 分别与每个Ti弱相容。ψ:X×X →［0，∞)是对称有界连续函数，ψ(x，x)=0，∀x ∈X，若∀x，y ∈X，∀i，j ∈∧，i ≠j，有ψ(Ax，By)，其中，Φ 为右连续的压缩尺度函数，则A，B，Ti，i ∈∧在X 中存在唯一公共不动点。

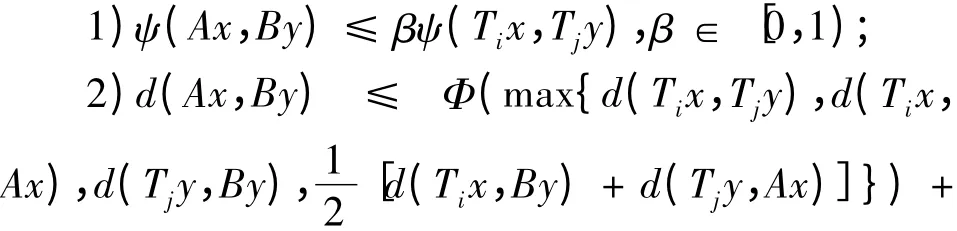
证 对i，j，m ∈I，i ≠j，i ≠m。由定理1 知A，B，Ti，Tj存在唯一的公共不动点xij，A，B，Ti，Tm存在唯一的公共不动点xim，由条件2)得

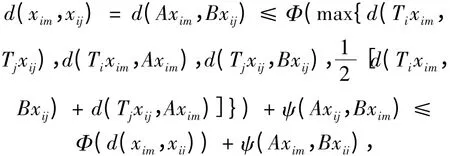
又由条件1)有

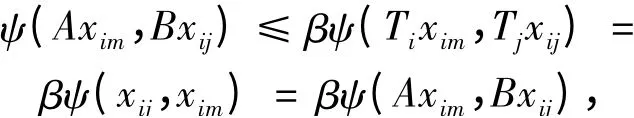
所以ψ(Axim，Bxij)= 0，从而

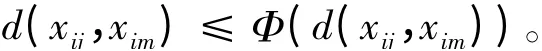
由引理1 知d(xij，xim)= 0，故xij= xim。由i，m 的任意性即得A，B，{Ti}i∈I在X 中有唯一公共不动点。定理3 设A，B，Ti(i ∈∧，指标集∧的势≥2)都是X 上的自映射，AX ⊆TiX，BX ⊆TiX 或(Ax ⊆TiX，BX ⊆TiX)，i ∈∧，A，B 分别与每个Ti可交换。ψ:X ×X →［0，∞)是对称有界连续函数，若存在正整数n，使∀x，y ∈X，∀i，j ∈∧，i ≠j，有ψ(Ax，By)，其中，Φ 为右连续的压缩尺度函数，则A，B，Ti，i ∈∧在X 中存在唯一公共不动点。

证 令A1= An，B1= Bn，则A1，B1分别与Ti可交换，从而也分别与Ti弱相容，故由定理2 即得。证毕。

注5 在定理2，定理3 中取Φ(t)在R+上单调不减，ψ(x，y)≡0 时即得文献［7］中的定理2 和定理3。

［1］Sessa S.On a weak commutativity condition in a fixed point considerations［J］. Publ Inst Math(Beograd)，1982，32(46):149-153.

［2］Jungck G.Compatible mappings and common fixed points［J］.Internat J Math and Math Sci，1986，9(4):771-779.

［3］Jungck G，Rhoades B. Fixed point for set valued functions without continuity［J］. Indian J Pure Appl Math，1998，29(3):227-238.

［4］李高明.一个新型不动点定理［J］.河北师范大学学报:自然科学版，1995，19(4):24-26.

LI Gaoming.A new fixed point theorem［J］.Journal of Hebei Normal University:Natural Science Edition，1995，19(4):24-26.(in Chinese)

［5］谷峰，高伟，田巍.不动点定理及非线性算子的迭代收敛性［M］.哈尔滨:黑龙江科技出版社，2002.

［6］陈仕洲.两对相容映射的公共不动点定理［J］. 宝鸡文理学院学报:自然科学版，2004(1):10-11.

CHEN Shizhou.Common fixed point theorems for two pairs of compatible mappings［J］. Journal of Baoji College of Arts and Sciences:Natural Science Edition，2004(1):10-11.(in Chinese)

［7］陈仕洲.度量空间弱相容映射的几个新的公共不动点定理［J］. 长春师范学院学报:自然科学版，2006，25(1):25-27.

CHEN Shizhou. Some new common fixed point theorems for weakly compatible mappings in metric spaces［J］. Journal of Changchun Teachers College:Natural Science，2006，25(1):25-27.(in Chinese)

［8］张石生.不动点理论及其应用［M］.重庆:重庆出版社，1984.

［9］ZHANG Y S，WANG L，Shin S H，et al.Common fixed point theorems for a pair of orbitally contraction mapping［J］.Fixed Point Theory and Applictions，2003，5:191-195.

［10］郑晓迪，万美玲，张树义.轨道压缩映射的几个新的不动点定理［J］.北华大学学报:自然科学版，2014，15(4):438-442.

ZHENG Xiaodi，WAN Meiling，ZHANG Shuyi. Some new fixed point theorems of orbitally contraction mappings［J］. Journal of Beihua University:Natural Science，2014，15(4):438-442.(in Chinese)

［11］张树义，赵美娜，李丹. 关于平方型Altman 映象的公共不动点定理［J］. 江南大学学报:自然科学版，2015，14(4):472-477.

ZHANG Shuyi，ZHAO Meina，LI Dan. On common fixed point theorems for twice power type Altman mapping［J］. Journal of Jiangnan University:Natural Science Edition，2015，14(4):472-477.(in Chinese)

［12］张树义，宋晓光，栾丹.Φ-压缩映象的公共不动点定理［J］.北华大学学报:自然科学版，2014，15(2):167-173.

ZHANG Shuyi，SONG Xiaoguang，LUAN Dan. Common fixed point for contraction mapping［J］. Journal of Beihua University:Natural Science，2014，15(2):167-173.(in Chinese)