基坑支护插入深度及刚度对变形影响的有限元分析

王峻科， 陈志坚 ， 荀志国

(河海大学 地球科学与工程学院，江苏 南京210098)

近年来，随着我国城市化进程的推进，城市的土地资源变得更加宝贵，因而为了增加土地利用率，大量的高层及超高层建筑开始兴起，同时对地下空间的开发利用也成为热点。伴随而来的第一个问题就是基坑的设计和施工。基坑开挖不仅要保证基坑本身的安全与稳定，而且要较好地控制基坑周围土体的变形来保护周围建筑及公用设施的安全和正常使用。

在城市基坑工程设计中，对基坑变形的控制要求越发严格，之前的设计方案大多以强度控制为主，如今逐渐被以变形控制设计为主的方式所取代，所以对基坑变形进行分析已成为基坑设计中的一个非常重要的部分［1］。而有限单元法作为模拟变形的重要手段，在基坑研究中得到了广泛的应用。为此，文中试图通过有限元软件模拟基坑变形，得到影响其变形的相关因素及变化规律，以期对今后基坑设计具有一定参考作用。

1 有限元模型建立

1.1 本构模型

采用的有限元计算软件为ABAQUS 软件;本构模型选用Mohr-Coulomb Model(摩尔库伦模型)，摩尔库伦模型屈服面函数:

式中，φ 是q-p 应力面上Mohr-Coulomb 屈服面的倾斜角大小，0° ≤φ ≤90°;c 是材料的黏聚力。其中Rmc(Θ，φ)限制屈服面的形式，按照下面式子进行计算:

图1 Mohr-Coulomb 模型中的屈服面Fig.1 Yield surface of the Mohr-Coulomb model

由图1 可见，Mohr-Coulomb 屈服面存在尖角，在相关联的流动法则(塑性势能面与屈服面相同)之下则会在尖角处出现塑性流动方向不唯一的情况，导致数值计算出现很差的收敛性。为了防止数值结果在这些奇点上出现收敛缓慢等问题，ABAQUS 软件选择用连续光滑的椭圆函数作为塑性势面，如图2 所示［2］。

图2 Mohr-Coulomb 模型中的塑性势Fig.2 Plastic potential surface of the Mohr-Coulomb model

塑性势函数为

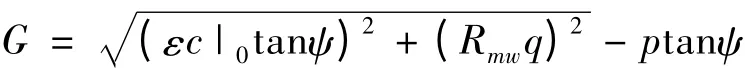
式中ψ 为剪胀角，c |0为初始黏聚力即为没有塑性变形的黏聚力。ε 是子午面上的偏心率，它控制G 在子午面的形状与函数渐近线之间的相似度。如果ε =0，塑性势能面在子午面上是一条倾斜向上的直线，ABAQUS 中默认为0.1。Rmw(Θ，e，φ)则控制了在π 平面的形状，其计算公式如下:

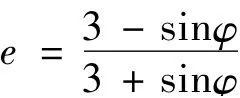
计算。e 可保证塑性势能面在π平面受拉和受压的角点处实现光滑化。当然文中也可以指定e 的大小，其范围为0 ＜e ≤1。硬化规律由ABAQUS 中通过控制黏聚力c 的大小来实现Mohr-Coulomb 模型屈服面大小的变化，即硬化或软化，用户必须指定等效塑性应变与黏聚力c 之间的变化关系，通常通过表格输入［2］。

1.2 模型参数

为了更贴近实际的施工条件，本模型选取3 种性质的土层，表1 为土层参数。

表1 选用土层的建模参数Tab.1 Model parameters of the selected soil

拟定基坑的开挖深度为10 m，采用悬臂式支护结构，分4 次开挖，第1 次开挖1 m，之后每次开挖3 m。因为支撑越多，支护插入深度对变形的影响就越小，所以采用单道支撑既能很好地模拟实际工况，又能明显反映出变形特点［3］。

1.3 模拟计算

一般模拟连续墙时，采用二维梁单元，文中则是用实体单元，更符合实际工况，能更好地模拟土体与墙体的接触关系［4］。下文将以连续墙长度为20 m，宽度为0.7 m 的设计方案为例进行建模。

在进行数值模拟时，初始应力场是最重要的，是正确模拟施工过程的先决条件。初始应力的加载必须满足地应力平衡，因此需要进行地应力平衡分析。图3 为地应力平衡时的土层竖向应变云图。

图3 地应力平衡时土层竖向应变Fig.3 Vertical strain contours of the soil when the in-situ stress is balance

由图3 可以看出，当土体的竖向位移基本在10－5～10－3数量级之内，表明土体的竖向位移基本很小，已经达到平衡且符合实际情况［5］。

下面通过控制生死单元来进行基坑开挖模拟。第1 层开挖深度为1 m，开挖后墙土体的水平位移变化如图4 所示。

第2 层开挖深度为3 m，开挖后墙土体的水平位移变化如图5 所示。

施加单道支撑，然后进行第3 层开挖，开挖深度为3 m，开挖后墙土体的水平位移变化如图6 所示。

第4 层开挖深度为3 m，开挖后墙土体的水平位移变化如图7 所示。

图4 第1 级开挖后墙土体的水平位移Fig.4 Horizontal displacement contours of the soil wall after first excavation

图5 第2 级开挖后墙土体的水平位移Fig.5 Horizontal displacement contours of the soil wall after second excavation

图6 第3 级开挖后墙土体的水平位移Fig.6 Horizontal displacement contours of the soil wall after third excavation

图7 第4 级开挖后墙土体的水平位移Fig.7 Horizontal displacement contours of the soil wall after fourth excavation

通过观察各个阶段的水平位移云图可以看出，连续墙的水平位移最大值出现在第2 次开挖后，之后通过施加单道支撑，有效地减小了其水平位移，使墙体更为稳定［6］。

2 插入深度及刚度影响分析

下面通过改变连续墙的插入深度及刚度来探讨这些条件对变形的影响。连续墙的插入深度分别取7，10，13，16 m，建立有限元模型，计算出开挖后墙体的水平位移值。图8 为连续墙不同插入深度下的水平位移变化。

图8 连续墙不同插入深度下的水平位移曲线Fig.8 Horizontal displacement curve of the continuous wall under different insertion depth

从模拟结果来看，通过增加连续墙的插入深度，能有效地减小其水平位移，使结构更加稳定。当深度大于10 m，其稳定效果变得不太明显，所以并不是连续墙插入深度越大越好，而是应该找到最合理的插入深度，既能保证结构体的安全稳定，又能节约施工成本增加效率。从图8 可以看出，10 m 至13 m 的插入深度是比较合理的。在每步开挖结束后，及时施加支撑也能减小水平位移，同时减小插入深度对水平位移的影响，也是符合实际施工情况的考量方案［7］。

在研究刚度对变形的影响时，先确定连续墙长度为20 m，然后改变刚度，连续墙刚度EI 分别取9 ×104，3 ×105，9 ×105，1.5 ×106kN·m2，建立有限元模型进行计算。图9 为不同刚度连续墙的水平位移变化。

由图9 可以看出，随着连续墙刚度的增加，其水平位移不断减小，尤其是未插入土体部分，位移减小尤为明显。当连续墙刚度较小时，增加其刚度对减小水平位移有比较明显的效果，特别是对于未插入土体的部分尤为显著。不过，当刚度达到一定值后，这种减小位移的效果就开始不明显了。由此可见，在应用到实际工程中，不能为了减小连续墙的水平位移，提高结构稳定性而一味增大墙体刚度［8］。

图9 连续墙不同刚度下的水平位移曲线Fig.9 Horizontal displacement curve of the continuous wall under different stiffness

3 结 语

从模拟结果来看，增加插入深度和墙体刚度都对减小变形、提高稳定性有显著作用，然而在达到一定程度后，这样的作用就开始减弱，同时在开挖过程中及时施加支撑也是有效地提高结构稳定性的方法。在基坑支护设计时，一定要根据实际条件选择最合适的插入深度和刚度，以及施加支撑的道数和位置，既能保证结构体稳定，又能节约施工成本。

有限元模拟计算在基坑设计和研究中的应用将会越来越普遍，得到的计算结果也具有重要的参考意义。文中运用ABAQUS 软件进行模拟计算，为了更接近实际工况，不是用简单的梁单元来模拟连续墙，而且采用实体单元，更准确地模拟墙土体的接触关系［9］。对于土体单元也采用了3 种不同性质的土层，并且进行分层不均匀开挖，这些都符合施工实际，得到的结论更具参考价值。

［1］赵花丽，傅少君.深基坑工程的现状与发展［J］.孝感学院学报，2005，25(3):94-96.

ZHAO Huali，FU Shaojun.Status quo and prospect of deep fuondation pit engineering［J］.Journal of Xiaogan University，2005，25(3):94-96.(in Chinese)

［2］费康，张建伟.ABAQUS 在岩土工程中的应用［M］.北京:中国水利水电出版社，2010:67-70.

［3］朱向荣，王金昌.ABAQUS 软件中部分土模型简介及其工程应用［J］.岩土力学，2004，25(22):144-148.

ZHU Xiangrong，WANG Jinchang.Introduction to partly soil models in ABAQUS Software and their application to the geotechnical engineering［J］.Rock and Soil Mechanics，2004，25(22):144-148.(in Chinese)

［4］陈晶.基于ABAQUS 的桩土共同作用的数值模拟［J］.河南科学，2009(8):974-976.

CHEN Jing.The simulation of pile-soil interaction using ABAQUS［J］.Henan Science，2009(8):974-976.(in Chinese)

［5］秦会来，张甲峰，郭院成，等.ABAQUS 在计算基坑开挖变形中的应用研究［J］.岩土工程学报，2012(S1):82-86.

QIN Huilai，ZHANG Jiafeng，GUO Yuancheng，et al. Application of ABAQUS in calculating deformation of excavations［J］.Chinese Journal of Geotechnical Engineering，2012(S1):82-86.(in Chinese)

［6］张运良，聂子云，李凤翔，等.数值分析在基坑变形预测中的应用［J］.岩土工程学报，2012(S1):113-119.

ZHANG Yunliang，NIE Ziyun，LI Fengxiang，et al.Deformation prediction of excavations based on numerical analysis［J］.Chinese Journal of Geotechnical Engineering，2012(S1):113-119.(in Chinese)

［7］马平，申平，秦四清，等.深基坑桩锚与土钉墙联合支护的数值模拟［J］.工程地质学报，2008(3):114-120.

MA Ping，SHEN Ping，QIN Siqing，et al.Numerical simulation of pile-anchor and soil nailing wall composite support structure in deep foundation pit［J］.Journal of Engineering Geology，2008(3):114-120.(in Chinese)

［8］张浩龙，李柏生，任永忠，等.深基坑土钉和桩锚支护数值模拟分析［J］.兰州理工大学学报，2012，38(6):123-128.

ZHANG Haolong，LI Bosheng，REN Yongzhong，et al. Numerical simulation and analysis of soil nailed wall and pile-anchor supporting structure for deep foundation excavation［J］.Journal of Lanzhou University of Technology，2012，38(6):123-128.(in Chinese)

［9］平扬，白世伟，徐燕萍.深基坑工程渗流-应力耦合分析数值模拟研究［J］.岩土力学，2001，22(1):37-41.

PING Yang，BAI Shiwei，XU Yanping.Numerical simulation of seeapage and stress coupling analysis in deep foundation pit［J］.Rock and Soil Mechanics，2001，22(1):37-41.(in Chinese)