动水压力对高桩平台的动力响应

陈光明， 张淑华 ， 袁 宇， 刘春阳， 孙兴毅

(河海大学 港口海岸与近海工程学院，江苏 南京210098)

桩基平台具有抵御波浪和地震的能力，广泛应用于海洋石油开采。深水桩基平台在地震作用下会引起结构周围水体的辐射波浪运动，水体波动将对桩基平台水下部分产生动水压力。该动水压力不仅会改变结构的动力特性，还会影响结构的动力响应［1-2］。因此，动水压力问题是一个十分复杂的问题。

目前国内外学者对深水中桩柱结构动水压力方面做了不少研究。罗传信等［3］进行波浪与地震响应研究，分析得出动水阻尼对大波高、长周期波浪荷载下平台响应影响较大，在进行动力分析时应加以考虑。高学奎［4］采用附加质量的方法，结合有限元方法来分析深水桥墩的地震响应，认为地震动水压力对深水桥墩的影响是显著的。刘洋［5］利用ADINA 软件建立导管架海洋平台有限元模型，分析表明考虑附加水质量和动水阻尼能够减小平台的频率，并且验证得到阻尼对平台的频率影响很小。李富荣等［6］在Morison 方程的基础上，以单柱式桥墩为研究对象，用附加水质量法考虑动水压力对桥墩的影响，结果表明考虑动水压力效应是有必要的。前人研究主要集中水体阻尼及水体附加质量引起的水体惯性力对结构动力响应的影响，很少考虑桩土非线性作用。文中根据动力时程分析法的基本理论，基于Ansys 有限元软件，建立桩基平台-土三维模型，分析附加水质量和动水阻尼对桩基响应的影响规律，并比较桩基空间布置及倾斜方位对其内力的影响规律。

1 高桩承台有限元模型和荷载环境

1.1 高桩承台工程概况

针对某一工程为研究对象，承台厚度2 m，采用9 根3 ∶1 斜桩，泥面处高程为0 m，桩底高程－42 m。高桩承台布置见图1，桩基布置见图2 和表1，有限元模型见图3，土层物理性质参数如表2 所示。

图1 高桩承台布置Fig.1 Location of the elevated pile cap

图2 桩位置布置Fig.2 Location of the pile

表1 桩的空间位置布置Tab.1 Spatial position of the pile arrangement

图3 有限元模型Fig.3 Finite element model

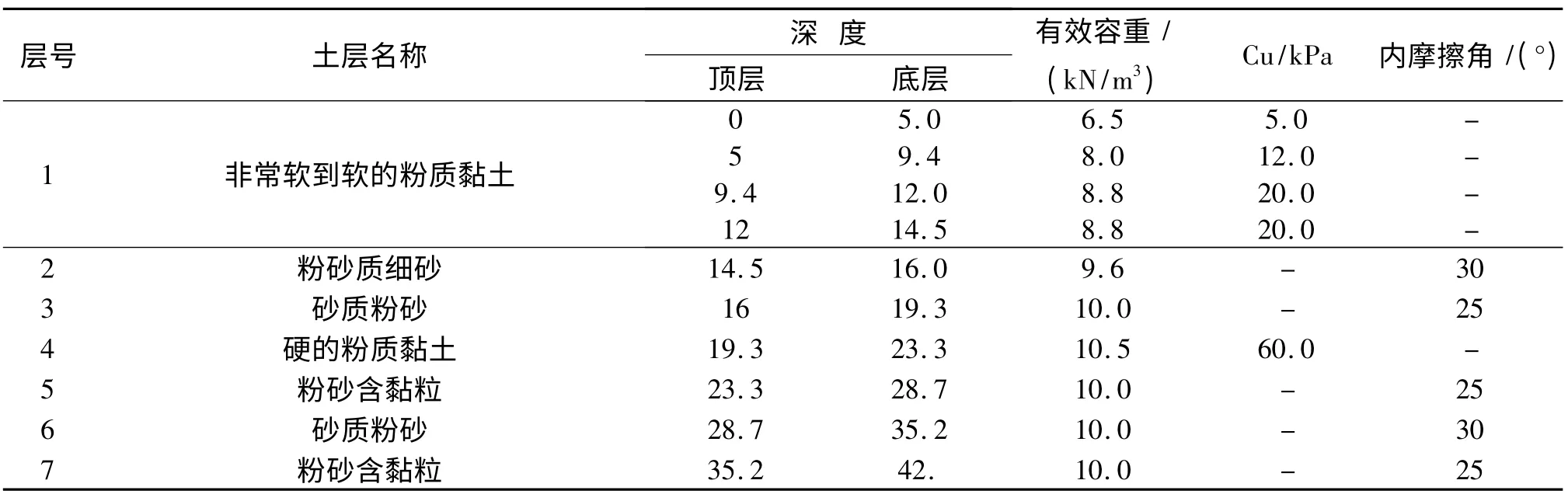
表2 土层物理性质参数Tab.2 Parameters of the soil physical property

1.2 高桩承台有限元模型

承台结构材料为C40 混凝土，采用solid95 单元，单元尺寸为1 m。桩基材料为Q235B 钢管桩，直径为0.5 m，壁厚18 mm，采用beam188 单元，单元尺寸为1 m。

1.3 荷载环境

1.3.1 动水压力荷载 以Morison 方程为基础，把水等效为附加质量来考虑水对结构的影响，忽略桩基对海水运动的影响，认为海水对桩基的作用由未受扰动的加速度场和速度场引起的沿水运动方向作用于桩基上的惯性力和阻尼力所引起，采用简化的Morison 方程表示地震动引起的桩基动水压力:

其中，MW= (CM－1)ρV 为动水附加质量系数，CW=0.5CDρAPσ为动水附加阻尼系数。则节点i 处等效附加水质量为

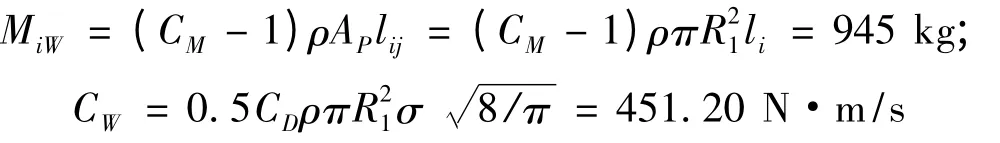
式中，海水密度ρ 取1.2 ×1.03kg/m3，R1为钢管桩的外径0.5 m，li为第i 单元有效长度为1 m，《海港水文规范》［7］对于圆柱体结构取CM= 2.0，CD=1.2，σ = 0.5。

文中附加水质量采用MASS21 单元模拟，动水阻尼采用COMBIN14 模拟，桩土非线性作用采用COMBIN39 模拟，具体如图4，5 所示。

1.3.2 地震荷载 文中选取前10 s 时间内EL-Centro 波，且只考虑水平地震荷载作用。该区域地震设防烈度为8 度，地震波的调幅系数为0.2 g，需对加速度曲线上每个点乘以0.2 g 后施加于结构上(见图6)。

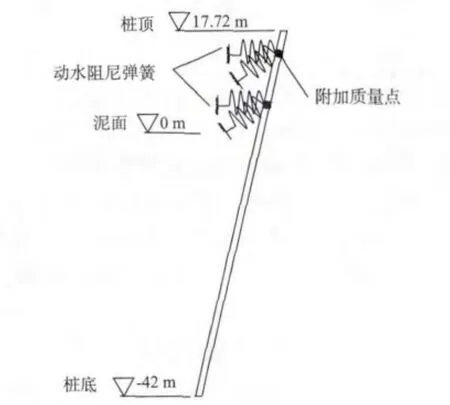
图4 动水压力分析模型Fig.4 Hydrodynamic pressure analysis model

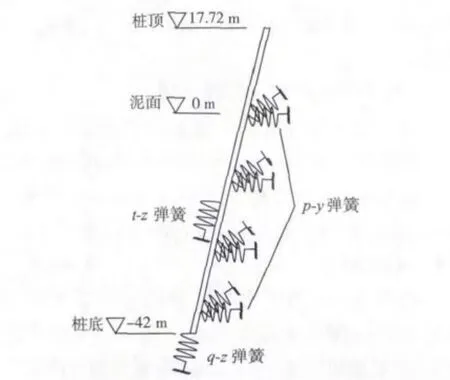
图5 桩土非线性模型Fig.5 Nonlinear model of the pile-soil

图6 EI-Centrol 地震波输入Fig.6 Time-history curves of the EI-Centrol motion

2 桩土非线性作用和模态分析

埋入土壤的桩基部分所受土壤非线性作用力通过非线性弹簧单元COMBIN39 模拟。桩基和土体之间的阻尼系数为0.02。根据表2 中的内摩擦角、不排水抗剪强度等参数，结合《海上固定平台规划、设计和建造的推荐作法工作应力设计法》［8］，计算出桩土的横向荷载-位移传递曲线(p－y 曲线)、轴向荷载－位移传递曲线(t－z 曲线)以及桩端荷载－位移传递曲线(q－z 曲线)，然后将荷载－位移传递曲线离散建立非线性弹簧单元实常数。沿桩基横截面x，y 方向施加单元长度为1 的非线性弹簧，沿桩的轴线方向施加单元长度为1 的非线性弹簧，具体见图4，5。

2.1 桩土侧向荷载-位移传递曲线

根据室内三轴试验和现场试桩桩周土极限土抗力一半时的桩挠曲变形y50= Aε50B，式中:A =2.5，B = 0.5 m，ε50= 0.02。

极限水平土抗力沿桩身分布，当x ＜xr，pu=3Cu+ γx + JCux/B，x ＞ xr，pu= 9Cu，其中xr=6B/(γB/Cu+ J)，x 为从泥面算起的任意深度，J =0.5。

水下软黏土在周期荷载作用下，当y ＜3y50时，pu= 0.5(y/y50)1/3;当y ≥3y50时，分为两种情况:(1)x ≥xr时，p = 0.72pu;(2)x ＜xr时，当y ≥15y50，p = 0.72pu(x/xr)，3y50＜ y ＜ 15y50，为 一直线。

2.2 桩土轴向荷载－位移曲线

对于打入黏性地基的桩，其桩身侧摩阻力fs和桩端极限阻力qp的一般表达式:fs= αCu，qp= 9Cu，当ψ ≤1.0，α = 0.5ψ－50，当ψ ＞1.0，α = 0.5ψ－0.25，式中，ψ = Cu/P0，P0为相应点的有限覆盖土压力。

2.3 模态分析

利用Ansys 做动力时程分析时需要采用Alpha阻尼和Beta 阻尼来定义瑞利(Rayleigh)阻尼常数α和β。阻尼矩阵是在用这些常数乘以质量矩阵［M］和刚度矩阵［K］后计算出来的。通常α 和β 值不是直接得到的，而是用振型阻尼比ξi计算出来的。ξi是某个振型i 的实际阻尼和临界阻尼之比。根据《建筑抗震设计规范》［9］的规定:文中取ξ1= ξ2= 0.05。

其中，ωi为结构的第1 阶和第2 阶自振频率，如表3所示。

表3 结构自振频率Tab.3 Natural frequencies of the structures

3 有限元分析结构与分析

3.1 动水压力对高桩承台结果分析

为了分析高桩承台动水压力的影响，分别计算考虑附加水质量和动水阻尼、考虑附加水质量但不考虑动水阻尼、不考虑附加水质量也不考虑动水阻尼时各桩基的位移峰值和桩顶弯矩峰值，计算结果如表4，5 所示。

表4 位移峰值Tab.4 Peak of the displacement

从表4 可知，沿地震波传播方向的同一列桩基同时达到最大水平位移，且大小相等。附加水质量使平台位移峰值增大20% 左右，动水阻尼使平台位移峰值减小－14% 左右，同时考虑附加水质量和动水阻尼时，桩1、桩4、桩7 号桩平台位移峰值增大4.10%，桩2、桩5、桩8 号桩平台位移峰值增大2.78%，桩3、桩6、桩9 号桩平台位移峰值增大1.12%，且共同作用时不具有线性叠加效应。

根据表5 中桩1 ～桩9y 方向和z 方向的峰值弯矩可知，附加水质量和动水阻尼对弯矩峰值的减小趋势与桩空间布置存在一定的相关性。桩1 和桩2平行，桩1 和桩2 的增大或减小效应相似;y 方向的峰值弯矩减小8.8% 左右;z 方向的峰值弯矩减小3.5% 左右;桩3 和桩1 沿地震加速度传播方向上空间对称，y，z 方向的峰值弯矩减小幅度呈现反对称趋势。桩4 和桩5 近似平行，y 方向的峰值弯矩减小幅度具有相似性。桩6、桩8、桩9 倾斜方向近似相同，y方向和z 方向的峰值弯矩减小11% 左右。桩7 与桩8沿地震加速度传播方向上空间对称，y 方向的峰值弯矩减小6% 左右，z 方向的峰值弯矩减小15%。综上可得，当桩基空间位置平行时，桩顶弯矩峰值存在相似的增大或减小趋势，当桩基之间近似空间对称时，则出现相反的规律。总之，附加水质量使弯矩峰值增大，且增大效应不明显，动水阻尼使弯矩峰值减小，减小效应明显，两者共同作用时具有线性叠加效应。

表5 弯矩峰值Tab.5 Peak of the bending moment

3.2 考虑附加水质量和动水阻尼作用下各方位桩之间内力分析

根据桩身弯矩峰值表，弯矩最大值发生在t =2.28 s 附近，此时加速度指向X 负方向，根据水平荷载作用方向和桩倾斜方向，此时桩1 ～桩5 为正斜桩，桩6 ～桩9 为负斜桩。

桩1 和桩2 空间平行，桩1 和桩3 关于桩2 所在的铅直面空间对称。图7，8 表明，桩3 的弯矩峰值最小，桩1 的弯矩峰值最大，桩2 总体与桩1 的弯矩和位移相似，在桩顶附近有部分差异。桩7 和桩8 关于它们之间的铅直面空间对称，桩8 和桩9 空间近似平行。图9，10 表明，桩7、桩8、桩9 的弯矩峰值图基本重合，泥面以上桩9 位移峰最大，桩7 的位移峰值最小，泥面以下3 根桩位移峰值图基本重合。图7，9表明负斜桩和正斜桩承受方向相反，且负斜桩比正斜桩能承受更大的弯矩。图11 表明沿地震加速度传播方向上，桩顶位移相同。

图7 1 ～3 号桩弯矩峰值Fig.7 Peak of the bending moment on 1 ～3 piles

图8 1 ～3 号桩位移峰值Fig.8 Peak of the bending moment on 1 ～3 pile

图9 7 ～9 号桩弯矩峰值Fig.9 Peak of moment on 7 ～9 piles

图10 7 ～9 号位移峰值Fig.10 Peak of displacement on 7 ～9 piles

图11 1，4，7 号桩位移峰值Fig.11 Peak of displacement on 1，4，7 piles

4 结 语

基于Ansys 有限元软件，建立了桩基平台-土系统的地震反应分析三维有限元模型。通过p－y，t－z，q－z 曲线考虑桩土之间的非线性作用，重点比较了附加水质量和动水阻尼高桩承台的位移和桩基内力影响，并讨论了桩基空间布置对结构内力影响，结果如下:

1)附加水质量使弯矩产生小幅度的增大效应，动水阻尼使弯矩产生较大的减小效应，且占主导地位，两者共同作用时具有线性叠加效应。

2)附加水质量使位移产生增大效应，动水阻尼使弯矩产生较大的减小效应，且附加水质量产生的增大效应大于动水阻尼的减小效应，两者共同作用时不具有线性叠加效应。

3)沿地震传播方向上，同一列桩的桩顶位移基本相同。

4)附加水质量和动水阻尼对桩基弯矩峰值的增大或减小效应存在一定的相关性，当桩基空间位置平行时，桩顶弯矩峰值存在相似的增大或减小趋势，当桩基之间近似空间对称时，则出现相反的规律。

5)在考虑桩土非线性和动水压力作用时，高桩承台桩基正斜桩的承载力大于负斜桩的承载力。

［1］唐寰澄.世界跨海工程概况［C］//中国土木工程学会桥梁及结构工程学会第十二届年会论文集(上册).广州:中国土木工程学会，1996:93-103.

［2］J.F.威尔逊.海洋结构动力学［M］.杨国金，译.北京:石油工业出版社，1991.

［3］罗传信，刘春山，唐红英.动水阻尼对桩基平台动力响应的影响问题［J］.海报，1989(11):794-800.

LUO Chuanxin，LIU Chunshan，TANG Hongying.Dynamic water damping effect on dynamic response of pile foundation platform problem［J］.Journal of Posters，1989(11):794-800.(in Chinese)

［4］高学奎，朱晞.地震动水压力对深水桥墩的影响［J］.北京交通大学学报，2006，30(1):55-58.

GAO Xuekui，ZHU Xi. The influence of the vibration water pressure of deep water piers［J］. Journal of Beijing Jiaotong University，2006，30(1):55-58.(in Chinese)

［5］刘洋.导管架海洋平台海啸荷载作用下的受力分析［D］.大庆:东北石油大学，2013.

［6］李富荣，陈国兴，王志华.考虑动水压力影响的单柱式桥墩地震反应分析［J］. 地震工程与地震工程震动，2008，28(2):114-121.

LI Furong，CHEN Guoxing，WANG Zhihua.Considering the influences of dynamic water pressure single column pier earthquake response analysis［J］.Earthquake Engineering and Engineering Vibration，2008，28(2):114-121.(in Chinese)

［7］交通部第一航务工程勘察设计院.JTS145-2-2013 海港水文规范［S］.北京:人民交通出版社，2013.

［8］海洋石油工程专业标准化委员会.SY T10030-2004 海上固定平台规划、设计和建造的推荐作法工作应力设计法［S］.北京:中国石油出版社，2004.

［9］中华人民共和国住房和城乡建设部.GB50011-2010 建筑抗震设计规范［S］.北京:中国建筑工业出版社，2010.