教师评价中的模糊综合评价法
2015-01-15谢燕明
亚太教育 2015年18期
文/谢燕明
一、对象集、因素集和评语集
在这里本校230 名教师为对象集,评价指标集为因素集U ={备课充分(u1),清楚易懂(u2),板书整洁(u3)} ,评价等级为评语集V = {优(v1),良(v2),中(v3),及格(v4),不及格(v5)} 。
二、确定因素集的权重分配向量
三、建立综合评价矩阵R~
根据待评教师的分数,对每一个评价指标分别构造隶属于v1,v2,v3,v4,v5的隶属分数,将230 名教师的评分按从小到大排列,平均分为三类L1,L2,L3,并求出L1,L2,L3的平均值ω1,ω2,ω3。
1、备课充分对教师评分最高分为98,最低分为40,ω1= 65,ω2= 75,ω3= 85,则指标u1的五个等级隶属函数为:

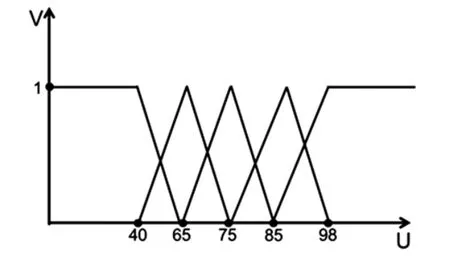
该待评价教师备课充分评分为90 分。则该教师在备课充分这个单因素评价为(0,0,0,0.62,0.38)。
2、清楚易懂对教师评分最高分为88,最低分为40,ω1= 63,ω2= 74,ω3= 85 ,则指标u2的五个等级隶属函数为:

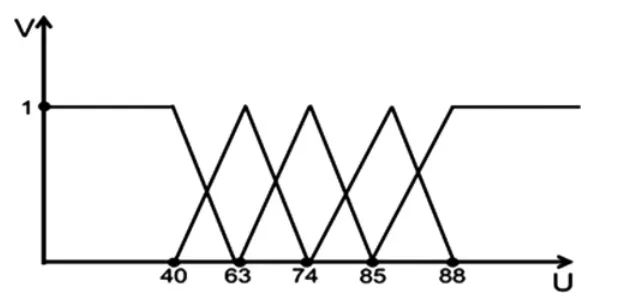
该待评价教师清楚易懂评分为70 分。则该教师在清楚易懂这个单因素评价为(0,0.36,0.64,0,0)。
3、板书整洁对教师评分最高分为100,最低分50,ω1= 70,ω2= 80,ω3= 90 ,则指标u3的五个等级隶属函数为:

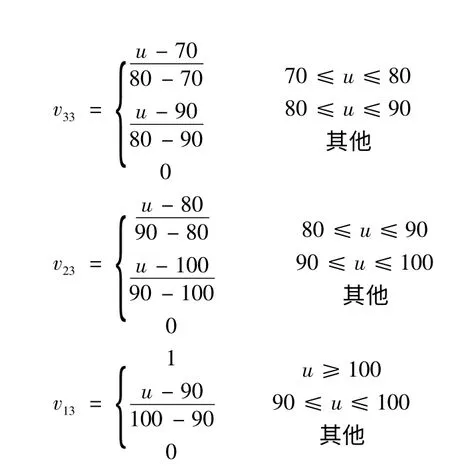
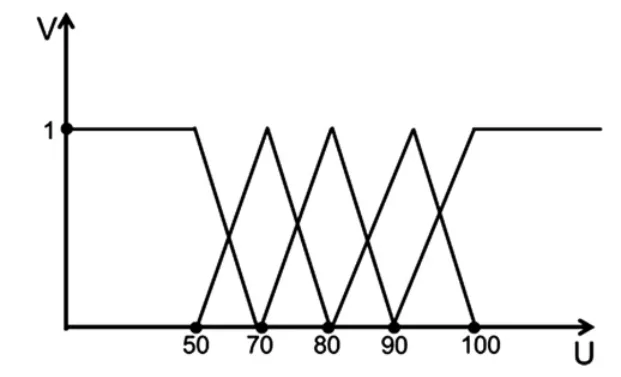
该待评价教师板书整洁评分为84 分。则该教师在板书整洁这个单因素评价为(0,0,0.6,0.6,0)。

模糊综合评价法不仅可以按综合分的大小对教师进行排序和分类,还可以利用模糊评价子集按最大隶属度原则直接判定教师的等级。
[1]秦寿康. 综合评价原理与应用[M] 电子工业出版社.2003. 6
