数形结合思想在高中解题过程中的运用

2015-01-15童光余

亚太教育 2015年18期

文/童光余

数学家华罗庚说“数与形，本是相倚依，焉能分作两边飞。数缺形时少直觉，形少数时难人微。数形结合万般好，割离分家万事非。切莫忘几何代数统一体，永远联系，切莫分离!”［1］，这句话恰到好处的阐述了数形结合的内涵， “数”可以把复杂问题简单化，是一种抽象思维;“形”可以把抽象问题具体化，是一种形象思维。数形结合就是抽象思维和形象思维的结合、相互之间的补充，从而培养解决问题的能力。在解决问题的过程中，要帮助学生习惯于、善于把数与形结合在一起考虑，既注意数的几何意义，也分析形的数量关系。根据问题的条件，实现数与形的相互利用，相互转化，从而更好的理解、掌握数形结合思想的实际内涵。

一、“形”化“数”，用代数来解决几何问题

几何图形虽然有形象、直观的优点，但在定量方面还必须借助代数的计算，用数论形，可以让学生理解图形几何意义下的数量关系。在高中数学立体几何解题过程中我们运用的向量法就是典型的例子，它通过建立空间直角坐标系把线线垂直和平行转化为向量垂直和平行的代数表达形式，把线面垂直和平行转化为线面中向量垂直和平行的代数形式，进而把几何问题转化为代数问题。

在三角函数中形化数的思想也有很重的运用，把几何图形中有关的边与角的关系式转化为二角函数的关系式，再借助于三角函数的有关概念与性质解决问题，如:

二、“数”化“形”，把数赋予几何直观

数是比较抽象的，我们难以把握，而形具有形象、直观的优点，能表达较多的思维。所以利用数形结合思想，把抽象的数转化为直观的图形，化难为易，利用图形来解决数的问题是一类常用的方法。

我们常用这种思想解决方程根的问题以及比较大小的问题转化为函数图像的问题，如:

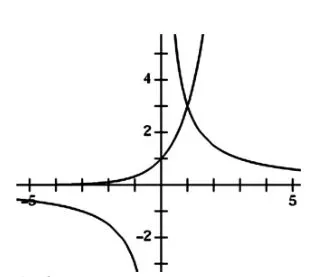
例四:比较y1= 2x、y2= x3和y3= lnx 当x=0. 5 时的大小

分析:前面两个的值可以通过计算大概的计算出来，但是第三个无法计算出来，所以不能够直接的比较第三者与前面这两个的大小关系。观察这三个值，会发现它们的形式和高中所学的指数函数、幂函数和对数函数十分相似，可以看成它们分别取0. 5、3 和0. 5 是的函数值，我们可以通过所学知识画出它们的函数图像，如图所示:从函数图像中很容易判断当x=0. 5 是三者之间的大小关系，y1＞y2＞y3。