基于已有经验组织活动,促进空间观念有效发展
2015-01-14赵斌
赵斌

案例背景:
图形与几何是小学数学四大领域内容之一,其教学目标之一就是促进学生空间观念的发展。如何结合学生的心理特征,立足并用好学生经验,处理好直观和抽象的关系,有效发展学生空间观念?这一问题一直是数学教师关注的热点。带着这些思考,笔者尝试着执教四年级下册《等腰三角形和等边三角形》一课。
片段一
师:前面我们已经研究了三角形,请大家回顾一下,三角形按角分类,可以分成几类?
生:三角形按角可以分成直角三角形、钝角三角形和锐角三角形。
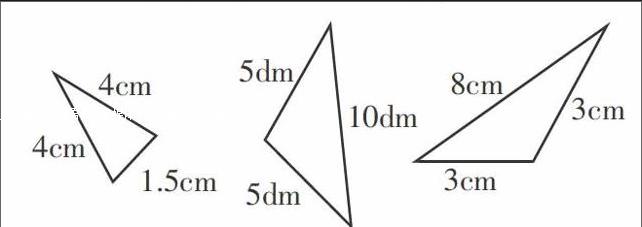
师:是的。下面请大家观察这三个三角形,它们各属于哪一类?
出示三个三角形:
生(齐答):第一个是锐角三角形,第二个是直角三角形,第三个是钝角三角形。
师:判断得又准又快!请大家仔细观察,这三个三角形里还有一些没有学过的相同点,看看谁能快速、准确地找出来!
生:它们有两条边是相等的。
师:找得真快!是这样吗?请大家动动手,用尺子量一量。
学生用尺子量好后认为三个三角形都是有两条边相等的。
师:像这样的三角形,我们把它叫作等腰三角形。
思考:本课时是三角形单元的第五课时,学生在前面的学习中经历了将现实物体抽象为几何图形,进行了大量抽象图形的研究。课堂直接从对抽象图形的引入,呈现直观素材,引导学生观察,激起学生对已有抽象图形知识的经验,并有针对性地引导学生观察“没有学过的共同点”,聚焦观察点,让学生通过观察进行探究,通过操作进行验证,在经历观察和操作活动的过程中发展空间观念。
片段二
师:这三个三角形都是等腰三角形吗?
生(齐答):是等腰三角形!
师:它们形状不同,为什么都是等腰三角形呢?
生:因为它们都是有两条边的长度相等,所以都是等腰三角形。
师:看来你们对等腰三角形理解得挺深的!
教师再出示三个三角形:
师:这三个三角形是等腰三角形吗?
生(齐答):是等腰三角形。
师:你是怎么想的呢?
生:因为它们也都有两条边的长度是相等的。
师:一下子就抓住了等腰三角形的本质,真棒!
思考:教师运用变式原理,分层引导学生开展观察活动。通过两个问题情境的创设——形状不同为什么都是等腰三角形、位置变化为什么还是等腰三角形,引导学生在观察、对比和思考中抓住等腰三角形的本质属性,在深化对概念理解的同时,发展学生的空间观念和抽象思维能力。
片段三
师:三角形不用量,你能判断它是不是等腰三角形吗?
生:可以用折的方法。
师:你能具体说说你的想法吗?
生:只要将三角形对折,看看两条边是不是重合的,如果有两条边对折之后能够重合,就说明着两条边长度相等,就是等腰三角形。
教师结合学生回答将三角形纸对折演示。
师:这样的方法可以吗?
生:可以!
师:是的!这种方法不仅能够判断一个三角形是不是等腰三角形,还能自己制作一个等腰三角形。请大家打开书本,看着书上的步骤,自己剪一个等腰三角形。请大家一边剪,一边想:这样剪,为什么它就是一个等腰三角形?
学生操作,等学生操作完成后交流。
师:你们剪下的是等腰三角形吗?
生:是!
师:为什么它是一个等腰三角形呢?
生1:因为它是对折后剪下的。
生2:因为剪的时候两条边叠在一起,用一刀剪下的,长度肯定相等,所以一定是等腰三角形。
师:两位同学说的意思都对!两边重合,长度相等,当然一定是等腰三角形。
……
思考:在学生初步感知了等腰三角形的基础上,教师组织学生开展操作活动——剪等腰三角形,并引导学生在行为操作的过程中开展思维操作活动——这样剪为什么是等腰三角形?通过活动的开展,让学生进一步认识等腰三角形,积累操作经验和探究经验,并在此过程中提升学生的空间观念。
片段四
……
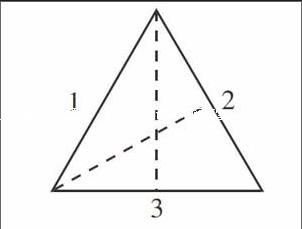
学生学习等边三角形,并在教师的引导下,按照教材上的图示,通过对折方法剪下一个等边三角形,教师展示一生作品。
(注:虚线表示其中的折痕)
师:我们在三条边上编上序号1、2、3,请大家思考一下,为什么不用量三条边的长度,剪下的就一定是等边三角形呢?
生沉思。
师:请大家观察一下剪下的三角形,里面有——
生:有两条折痕。
师:能否从这两条折痕中想到什么呢?
生:1、2两条边是相等的,因为它们在剪的时候是重合的;1、3两条边也是相等的,因为对折时它们也重合,所以它们三条边的长度相等。
师:大家听懂他的意思了吗?谁能再来说一遍?
生:我听懂了,他是说从第一次对折的折痕可以看出1、2两条边相等,因为剪的时候1、2两条边重合;第二次对折的折痕说明1、3两条边相等,因为剪的时候1、3是重合的。1、2相等,1、3也相等,所以2、3也相等,所以三条边都相等。
师:解释得真详细啊!除了通过折痕能看出三条边相等,还有什么发现呢?
生:还有三个角也是相等的,因为在对折的时候角也重合了。
师:大家能听懂他的意思吗?
生(齐答):能!
师:那么这三个角各是多少度呢?
生:这三个角都是60度,因为只要将180度除以3。
师:是的,等边三角形的三个内角都相等,只要将内角和180度除以3,每个内角都是60度。endprint
教师板书。
思考:教师继续组织学生进行动手操作——剪出等边三角形,并在操作后进一步引导学生进行推理,结合操作中形成的折痕证明这个三角形三条边的长度都相等,引导学生在行为操作的基础上进行表象操作,促进学生空间观念和推理能力的发展。
片段五
师:刚才我们一起认识了等腰三角形和等边三角形,以及它们各自的特征。请大家闭上眼睛,在脑子中画一个等腰三角形。
学生闭眼想象。
师:找到它的腰和底。
师:再找到它的底角、顶角。
师:再画一个不同的等腰三角形。
师:再画出几个不同的等腰三角形。
师:再画一个等边三角形。
师:找到它相等的三个角。
师:再画一个大点的等边三角形。
师:再画一个更大的等边三角形。
师:好!睁开你们的眼睛。
……
思考:认识了等腰三角形和等边三角形以及各自的相关概念、特征后,组织学生开展表象操作活动——闭上眼睛在脑子里画一画,并引导学生在“画”的过程中不断将图形进行变换,促进学生对概念本质属性的把握,同时促进学生对这两种图形表象的深刻建立,发展了学生的空间观念,也为后续更复杂的表象操作、符号操作,以及几何直观的形成奠定了基础。
“图形与几何”内容的教学是发展学生数学思维的重要载体,如何在小学数学课堂教学中发展学生的空间观念,并促进学生数学素养的提升?笔者结合案例认为:经验是基础,活动是关键,主要有以下策略。
一、学生经验的有效利用是空间观念发展的首要前提
小学生的几何知识来源于丰富的现实原型,除了在生活中,在学习中也积累了较为丰富的几何知识经验。这些是学生认识和理解几何图形、发展空间观念的基础,是教师教学的资源。因此,几何图形的起始学习经常从现实原型引入,激发学生已有的生活经验,逐渐对原型进行抽象。如果在前阶段已经历了这样的过程,并进行过抽象图形的活动,已有抽象图形操作的经验,也可以激发学生已有的知识经验,展开后续的学习、探究。
片段一中,教师以学生前段时间学习的知识经验为基础,通过问题予以激活,并展开新的探究活动,着眼于“都有两条边的长度是相等的”。已有经验的激活为学生展开新的探究做好了准备,有针对性的引导又为学生认知体系的拓展奠定了基础,而在此过程中,学生的空间观念也得以发展。
二、行为操作活动的有效开展是空间观念发展的必要环节
皮亚杰说过:儿童的思维是从动作开始的,切断动作与思维的联系,思维就不能得到发展。小学生空间观念及空间思维的发展也是如此。
片段一、二、四中,教师呈现了大量的直观素材,引导学生通过视觉活动认识几何图形。同时在片段三、四中,还分别组织了两次动手剪纸的活动,引导学生通过触觉活动认识几何图形。通过观察,让学生建立图形表象,获得对图形性质的理解,把握图形之间的联系;通过动手操作,让学生感知、发现,建构正确的空间形式和关系。这样在多感官参与的活动中,形成相应的空间表象,获得对几何知识的理解,建立和发展空间观念。
不管是视觉活动还是触觉活动,教师都要在此基础上引导学生思维的参与,让学生有针对性地进行活动,有助于学生深入地探究几何图形的特征,形成表象,发展空间观念。
三、表象操作活动的有效开展是空间观念发展的重要桥梁
学生通过观察、动手操作,初步获得了几何图形的表象。在此基础上,让学生直接有效地将获得的表象稳定地形成,为后续的符号操作提供表象基础,表象操作在行为操作和符号操作间的桥梁作用不可忽视。
片段五中,教师引导学生通过想象,在头脑中“画”不同的等腰三角形和等边三角形,有助于学生在表象操作中稳定、丰富表象雏形,形成正确的概念表征,为后续深入学习积累稳定而丰富的表象素材,发展学生的空间观念。
四、推理活动的有效开展是空间观念提升的主要渠道
推理是数学的基本思维方式。小学生几何学习过程中的推理很大程度上是依赖直观展开的,适时引导学生结合直观开展推理活动,有助于学生空间思维、几何直观能力和推理能力的发展。
片段三、四中,教师在引导学生开展了两次动手操作活动后没有止步:片段三中剪等腰三角形后,教师提出问题:“你们剪下的是等腰三角形吗?”引导学生结合操作过程进行证明;片段四中教师对学生推理能力的发展就显得更为突出,展示学生带有折痕的剪下的等边三角形,引导学生通过观察、思考,证明1、2两条边相等,2、3两条边相等,所以1、2、3三条边都相等。在这样的推理活动中,学生逐步认识了图形的特征及性质,推理能力、几何直观能力和空间观念都得以发展。?筻endprint
