让思维在操作后的思辨中向更深处漫溯
2015-01-14华丽芳
华丽芳
心理学研究表明:小学生思维的基本特点是从具体形象思维为主要形式逐步过渡到抽象逻辑思维。而培养抽象逻辑思维能力,是学生深刻理解和掌握数学知识的必要条件。因此,课堂教学中,教师要合理利用直观形象的手段,促进学生抽象逻辑思维能力的发展。
苏霍姆林斯基说过:“儿童的智慧在他的手指尖上。”动手操作可以让学生获取大量的感性认识,使抽象的数学知识形象化,有利于学生深刻理解和掌握所学的知识。但动手操作了,不表示思维就获得发展了,教师需要带领学生在直观操作的基础上根据教学内容进行理性思辨,才能使学生的思维逐步向更深处漫溯。下面,笔者结合“有余数的除法”一课的教学,谈谈自己的思考。
一、对操作结果据理分类,让思维更加有序
布鲁纳的多元表征理论认为:“对于一个数学概念可以有多种表征方式,多种方式之间要建立联系,才能深化对概念的理解。”
如“余数一定要比除数小”是“有余数的除法”的核心算理,要让学生真正理解这一算理的本质,首先要帮助学生建立余数这一概念。“有余数的除法”的教学注重引导学生在表内除法的基础上理解余数的含义,为此,教师教学时可通过对概念的不同表征方式,引导学生理解余数的含义。
教学片断:
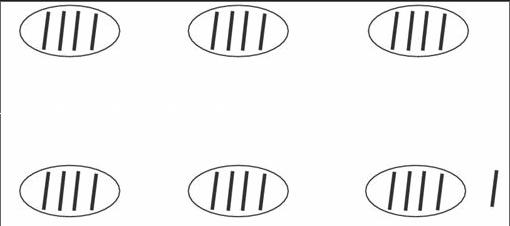
师:数学中有很多的平面图形,如果老师送你一些小棒,你想围哪些我们学过的平面图形呢?
生:三角形,正方形,五边形……
师:在这些图形中,老师最喜欢三角形。围1个三角形要用3根小棒,那10根小棒最多可以围几个这样的三角形?想试试吗?(生动手操作,师巡视)
师:谁来说说你是怎么围的?
生1:我用10根小棒围成3个三角形,还剩1根小棒。
师:10根小棒可以围3个三角形,那剩下的这1根小棒还能再围一个这样的三角形吗?为什么?
生2:不能。因为围一个这样的三角形需要3根小棒,现在只有1根小棒了。
师:你想用这10根小棒围正方形、五边形、六边形吗?(想)还是用刚才的这10根小棒,选择你最喜欢的一种图形围一围,围完后把你围了几个图形、还剩下几根小棒等情况,记录到你的表格里。(生动手操作)
师:谁来说说你是怎么围的?
生3:我用10根小棒围了2个正方形,还剩下2根小棒。
生4:我围的是五边形,围了2个,没有剩下小棒。
生5:我围的是六边形,围了1个,还剩下4根小棒。
……
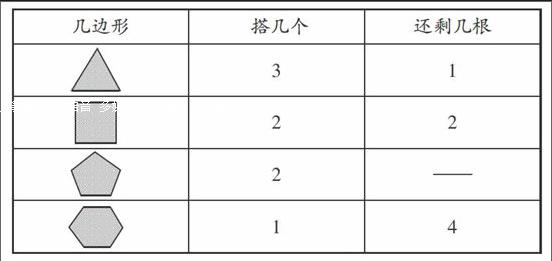
师(指下表):我们用10根小棒围不同的图形,得到了不同的结果,那你能根据这些剩下小棒的根数,把这四种情况分一分类吗?
■
生6:将剩下小棒的为一类,将没有剩下小棒的为一类。
师:为什么这样分?
生6:10根小棒围三角形、四边形、六边形到最后都有剩下小棒,而围五边形没有剩下小棒。
师:围三角形后还剩1根小棒,剩下的这1根小棒还能再围一个这样的三角形吗?为什么?
生7:因为围一个这样的三角形需要3根小棒,现在只有1根小棒了,所以围不成三角形。
师:围四边形后还剩下2根小棒,剩下的这2根小棒还能再围一个这样的四边形吗?为什么?
生8:因为围一个这样的四边形需要4根小棒,现在只有2根小棒了,所以围不成四边形。
师:围六边形后还剩下4根小棒,剩下的这4根小棒还能再围一个这样的六边形吗?为什么?
生9:因为围一个这样的六边形需要6根小棒,现在只有4根小棒了,所以围不成六边形。
师:看来,每5根小棒围一个五边形,10根小棒可以围2个五边形,正好用完小棒,你能用除法算式来表示吗?
生:10÷5=2(个)。
师:有剩余的情况也能用除法算式表示。
引导学生边交流边板书:
10÷3=3(个)……1(根)
10÷4=2(个)……2(根)
10÷6=1(个)……4(根)
师:比较一下,这3个算式和10÷5=2(个)有什么不同?
生:有剩下来的数。
师:这些剩下来的或者说多余下来的数叫余数,这就是我们今天要学习的“有余数的除法”。(师板书课题)
……
上述教学,教师先引导学生进行开放性的操作活动,再让他们根据剩下的小棒根数进行分类,最后交流分类的依据。在交流过程中,教师充分挖掘图表对学生思维有序引领的作用,顺利地把学生的注意力聚焦到余数这一关键点上,引导学生清晰地建立起余数这一概念。这样的思辨过程,给学生的思维以一种明确的方向性,培养了学生思维的有序性。
二、对操作结果分析比对,让思维更加灵敏
数学教学中,教师应找到教学的切入点,适时地利用操作结果的比对辨析,提升学生的思维水平,让操作与思维共融,培养学生思维的灵敏性。
“有余数的除法”一课的教学难点在于让学生理解“余数一定要比除数小”,所以在实际教学中,教师应抓住除数和余数这两个量的关系,组织学生进行如下操作。
教学片断:
师:12根小棒,每4根一份,可以分成这样的几份?(在黑板上画图,如下)
■
列算式:12÷4=3(份)
师:如果有13根小棒,每4根一份,会有什么结果?你能画一画,再列出算式吗?(生画后列式,如下)
■
列算式:13÷4=3(份)……1(根)
师:如果是14根、15根小棒,你会分吗?先画一画,再列式。(生进行操作活动)谁来汇报?
生1:14÷4=3(份)……2(根)。
生2:15÷4=3(份)……3(根)。endprint
师:比较一下,你有什么发现?
生3:除数都是4,余数不相同。
师:如果是16根小棒,每4根一份,可以分成几份?
生4:可以分成4份。
师:如果是17根小棒呢?
生5:可以分成4份,余1根。
师:如果是18根、19根小棒呢?
生6:18根小棒分成4份余2根,19根小棒分成4份余3根。
板书如下:
除数 余数
12÷4=3(份)
13÷4=3(份)……1(根)
14÷4=3(份)……2(根)
15÷4=3(份)……3(根)
16÷4=4(份)
17÷4=4(份)……1(根)
18÷4=4(份)……2(根)
19÷4=4(份)……3(根)
师:这些算式中的除数都是几?余数呢?
生7:除数都是4,余数分别是1、2、3。
师:余4根可以吗?
生8:不行,因为4根又可以分成一份。
师:余5根行吗?
生9:不行,因为5根还可以再分。
师:余6根、7根行吗?
生10:都不行,只有余3根、2根、1根可以。
师:这些数有什么共同点?
生:都比4小。
师:看来,在有余数的除法中,余数一定要比除数小。
……
上述教学,学生通过操作得出一组除数不变、被除数递增而引起余数递增的算式,教师将不变的除数和变化的余数进行比较,引导学生把思考的重点放在除数和余数上。在这一过程中,学生的思维被激活了,顺利地分析、归纳出余数的变化规律,教学的难点也就不攻自破。
三、对操作结果追溯反思,让思维更加深刻
受年龄特征的影响,小学生的思维容易停留在直观表象上,遇到问题不愿深入思考。因此,课堂教学中,教师要组织具有一定挑战性的操作活动,引导学生展开有效的讨论,帮助学生系统地理解和掌握算理,培养思维的深刻性。
本课教学中,在学生初步理解“余数一定要比除数小”的基础上,教师设计如下活动。
教学片断:
师:有一堆小棒,每几根分成一份,分成了5份,还剩4根,这堆小棒可能有几根?把结果填在下面的算式里。(生动手操作)
( )÷( )=5……4
生1:这堆小棒可能有29根。
师:你是怎么分的?
生1:我是每5根一份,分成5份是25根,再加上剩下的4根,一共是29根小棒。
师:可以每4根小棒一份去分吗?为什么?
生2:不可以。每4根小棒为一份,就不会有剩下的小棒了,因为剩下的4根小棒又可以分成一份。
师:可以每3根小棒为一份吗?
生3:也不可以。这样就不会剩下4根小棒了,因为4根里又可以再分出一份,余1根小棒了。
师:也就是说,至少每几根一份,才能保证这个算式成立?
生4:至少要满5根一份。
师:这就说明在有余数的除法里,除数一定要比余数大。
……
上述教学,教师打破原有的操作活动形式,直接给出操作的结果,让学生从结果出发进行推理,去追溯操作的过程。此时的操作,不再是教师指令下的动手活动,而是学生边推理边操作。这样的反例操作,既能帮助学生克服思维定式的影响,又能把操作和思维紧密结合起来,使“余数一定要比除数小”这一算理深深地印刻在学生的头脑里,学生的思维也在这样的活动中变得更加深刻。
有效的课堂教学,不仅需要设计切合学生发展的操作活动,更要重视操作后与学生针对操作结果所引发的每一次对话,使操作成为重要教学途径的同时,更是学生思维品质培养的触发点,从而促进学生的数学思维不断获得发展。
(责编 杜 华)endprint
