基于李群李代数的车用稳定平台加速度分析方法

刘 晓

（山西省交通科学研究院，山西 太原 030006）

0 引言

车载稳定平台能够隔离车辆受路面颠簸、车流量影响、发动机振动等环境扰动产生的六维扰动，为数字相机、激光传感器、光学仪器提供一个相对稳定的工作平台，已作为保障各类交通管制侦测车、多功能智能检测车工作精度的关键设备[1]。并联式稳定平台是一个处于非惯性系环境中的复杂多刚体系统[2]，一般由设备安装平台、运动执行器、铰链、基座构成，其中基座时刻随车振动。建立系统各刚体之间的加速度映射关系是分析设备稳定效果、建立运动学/动力学模型、制定稳定控制策略的前提，因此分析多刚体系统的加速度是开展稳定平台研究的前提。

传统运动学理论中通常使用三维矢量代数描述刚体的转动和移动，即刚体的加速度分别用它的角加速度和其上一点的线加速度来描述。由于这种传统的描述方法不具有坐标不变性，因此分析刚体加速度是一项繁琐困难的工作，特别是对于多刚体动力系统来说，这项工作就变得十分困难，另外，建立的复杂模型将导致算法耗时，严重影响稳定平台响应速度；采用Lagrange方法[3]分析刚体加速度时可回避上述问题，但该方法存在拉格朗日函数偏微分的求导这一繁杂的任务，实际上是将分析困难转移。

近年来，一些现代数学理论被应用于多刚体系统研究中，其中螺旋理论是一种有效的工具[4]。Ball最早建立了螺旋理论的基础，然而到目前为止，螺旋理论大多应用于刚体的速度、静力分析和几何综合，只有很少的工作将螺旋理论应用于刚体加速度分析中[5]。Bokelberg等讨论了速度螺旋的无穷小位移；Ridley等研究了刚体作一般运动时的加速度中心；Martinez和Duffy分析了刚体简化加速度的合成，并指出刚体的简化加速度具有坐标不变性。但直至目前，国际上对旋量的导数是不是刚体加速度这一问题的认识仍未统一，这也限制了其在分析多刚体系统时的应用[6]。

1 刚体加速度的六维旋量描述

令{a}和{b}分别为建立于刚体A和B上的坐标系，刚体B相对于A的速度在{a}系中的描述可定义为：

同时，式（1）是刚体B相对刚体A的运动旋量在{a}系中的六维矢量描述。在本文叙述过程中，左上标表示用于描述矩阵或矢量的坐标系，右下标表示相对运动或位置，如下标ab表示刚体B相对于刚体A的运动，也可表示点b相对于{a}系的运动或位置。展开式（1）可得：

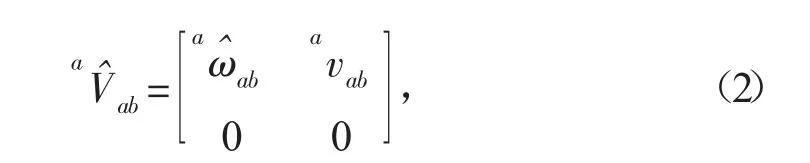
式中：

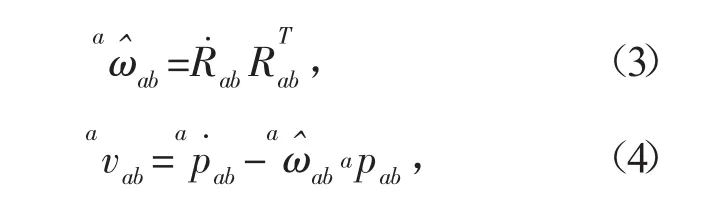
式中：aωab表示刚体B相对于刚体A的角速度，与传统的角速度表示一致；avab∈ℜ3是一个三维矢量，在本文定义为刚体B相对于A的线速度，与传统运动学理论中的线速度定义不同，avab并不是刚体B固连点b相对于{a}系的速度，而是刚体B上与{a}系原点瞬时重合点（设为a′）相对于{a}系的线速度，其数值与传统表示并不相同。因此，基于旋量理论建立的速度描述与传统运动学描述方式并不相同，在此称为刚体速度，其是一个包含角速度、线速度的六维矢量。

刚体B相对A的运动旋量求导即可得到对应的刚体加速度，对式（1）两端求时间导数可得：

对式（2）两端求时间导数：

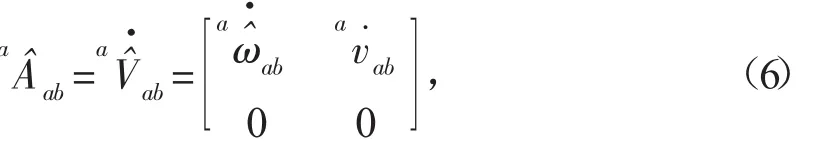
结合式（5）、式（6）建立刚体角加速度的旋量描述形式为：

令aaab=av˙ab，并定义aaab为刚体B相对于刚体A的线加速度，本文称为刚体线加速度，其与传统运动学描述方式的区别将在下节分析。由式（5）、式（6）建立其旋量描述形式为：

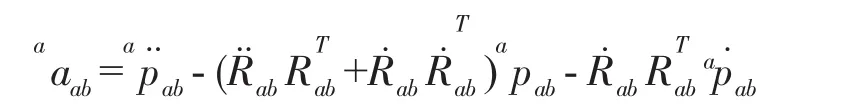
将式（3）、（7）代入上式，整理为：

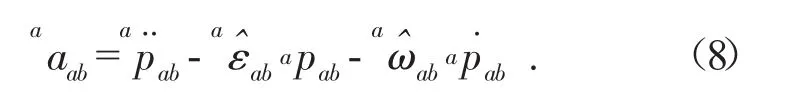
aaab∈ℜ3是一个三维矢量，依据李代数可证明刚体加速度表达式：

是李代数的一个元素，即aˆab∈se（3）为刚体的加速度旋量。

由于本文定义的刚体加速度旋量均是李代数空间的元素，因此李群空间元素gab的伴随作用可给出任意两个刚体加速度之间的变换，即存在以下关系成立：

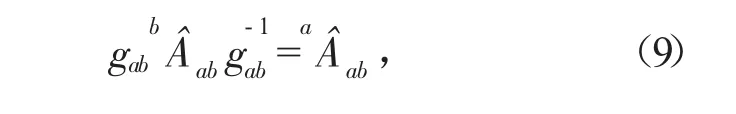
式中：bab为刚体B相对于A的刚体加速度在{b}系中描述。

上述提供了刚体速度、加速度的六维旋量描述和变换方法，后续的研究分析将证明这种描述方法在多刚体系统加速度中的优点。

2 刚体加速度的物理意义

本节将分析刚体加速度的物理意义，并与传统运动学描述方式进行对比。为了分析方便，令刚体B上与{a}系原点瞬时重合点为a'，并令αpba'为点b指向点 a′的位置矢量；ap˙aa′、ap¨aa′分别为点 a′相对于刚体A的瞬时速度、加速度。应用同一刚体上不同点之间的速度和加速度的变换公式可得到以下关系式：

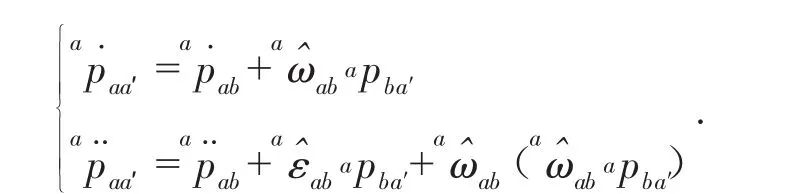
由点a′所处几何位置可到apba′=-apab成立，结合上式，刚体线加速度可整理为：

为了更明确地解释上式包含的物理意义，假设点s为刚体B螺旋运动轴线上的一点，apsa′为点s到点a′的位置矢量，如图1所示。依据螺旋理论点a′的速度可写为：

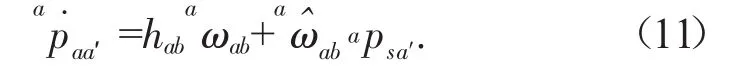
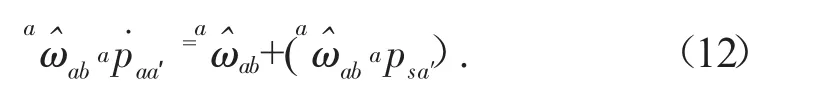
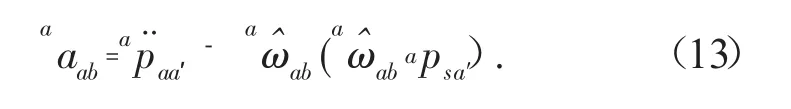
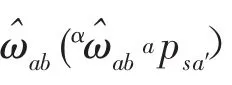
上述分析可以看出，刚体加速度的传统运动学描述是用刚体的角加速度和刚体上固定点的线加速度构成，而刚体加速度的旋量描述是由刚体的角加速度和刚体上瞬时与所用坐标系原点重合点的无向心加速度组成。上述两种描述方式的区别主要在于：a）刚体线加速度不是用刚体上某一固定点来分析描述，而是采用不同点来分析计算，即在运动过程中的各瞬时都采用与所用坐标原点重合的点进行描述；b）刚体线加速度数值大小为刚体上瞬时与所用坐标系原点重合点的无向心加速度。

为进一步明确刚体加速度的物理意义，结合点s、点a′，应用同一刚体上不同点之间速度和加速度的变换公式可得：

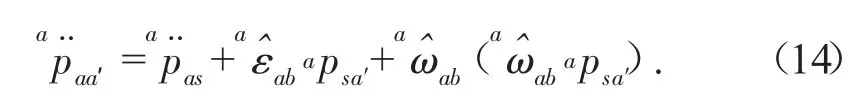
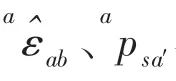
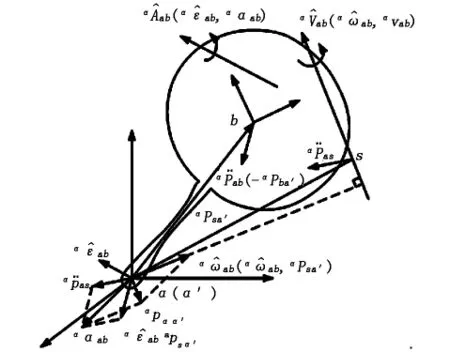
图1 刚体空间加速度的物理意义

将式（14）代入式（13），得到简化表达式为：

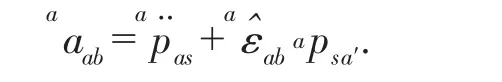
因此，刚体线加速度又可以看作是由刚体瞬时转轴上一点加速度和所用坐标系原点相对于瞬时转轴的切向加速度合成。

3 多刚体系统加速度伴随变换

基于上述建立的描述方法及物理意义，分析多刚体系统中各刚体加速度之间的运动变换关系，为建立并联式车载稳定平台运动学、动力学模型提供依据。

多刚体系统由3个刚体构成，分别为刚体A、B、C，对应的坐标系为{a}、{b}、{c}，{c}系建立于刚体 C上，gac、gbc分别为刚体 C相对于{a}系、{b}系的位姿变换矩阵，结合式（1），建立刚体C相对于刚体A的速度表达式为：

式中：g˙ac=g˙abgbc+gabg˙bc、gac－1=gbc－1gab－1.

通过对式（15）求时间导数，建立刚体C相对于刚体A的加速度表达式为：

对式（16）展开，结合式（1）、（5）、（15）将其整理为式（17）最简形式：

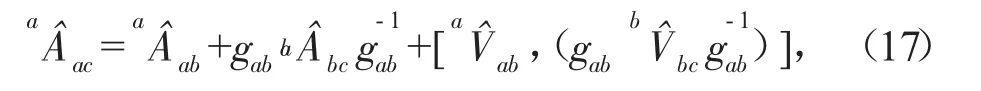
同理，使用相同的方法可建立刚体C相对于刚体A的加速度在{c}系中的表达式为：

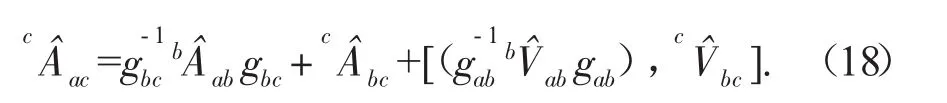
上述建立了当多刚体系统有3个刚体时，各刚体加速度之间的变换关系。将上述方法推广到多刚体系统中，令多刚体系统包含（n+1）个刚体，其中基座N0、运动刚体N1……Nn；惯性坐标系{0}与基座N0固连、非惯性坐标系{i}与第i个刚体Ni连接，如图2所示。由于篇幅有限，利用相同方法建立该系统第k个刚体相对于惯性坐标系{0}及非惯性坐标系{k}的加速度表达式为：

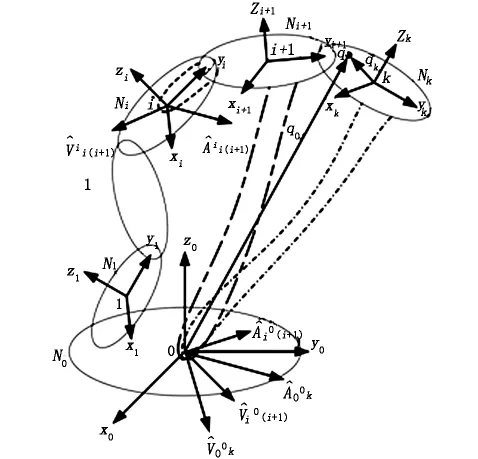
图2 多刚体系统速度、加速度描述

4 结论

a）基于运动旋量的李群表达式，给出了刚体加速度的旋量描述，并提供了刚体加速度在不同坐标系中的变化关系式。

b）揭示了所述刚体加速度的物理意义，即刚体角加速度与传统描述相同；刚体线加速度为刚体上瞬时与参考系原点重合点的无向心加速度，即该点加速度与其绕瞬时轴转动的向心加速度之差。

c）基于旋量的刚体动力学理论基础，导出了多刚体系统中各刚体加速度之间的伴随变换表达式，提供了一种分析复杂多刚体系统动力学的有效方法。

这些概念和公式为基于李群李代数直接采用六维表示分析非惯性系并联式车载稳定平台特性和动力学奠定了基础。