浅谈微积分思想及其在经济学中的应用

许天慧

（渤海大学数理学院，辽宁 锦州 121000）

数学作为科学的语言，不仅有着严谨的理论性，还具有较强的实践性。随着数学学科的发展，其诸多的理论、原理和公式等已经被广泛地应用到了经济学、管理学、天文学、理学、工学、医学等领域，为各个领域和学科的发展提供了科学的分析方法。微积分作为高等数学重要组成部分，在经济领域中也已得到了广泛地应用，在帮助经济主体实现成本最低化、利润最大化、贮存最优化等方面发挥出了重要作用。在本文中，即以微积分思想为研究出发点，对其在经济学中的重要性及典型应用案例进行了分析。

1 微积分思想概述

微积分是高等数学中研究函数的微分和积分以及相关概念的一个重要分支部分，同时，微积分也是高等数学中支撑其他分支学科、为其他学科提供计算方法的重要基础。微积分建立在实数、函数和极限等概念的基础之上，主要包括极限连续、可微分和积分等研究内容。微积分思想核心是“微元”和“无限逼近”。其中，微分学的核心思想是“无限细分”，积分学的核心思想是“无限求和”。

1.1 微分的基本思想

微分是对函数的局部变化率的一种线性描述，其基本思想的核心在于分析函数在足够小的范围内，能否来用线性函数来进行近似等同表示。其几何意义可以这样表述：设y=f（x）为是实函数，△x是函数中点A在横坐标上的增量，于此对应的△y为点A在纵坐标上的增量，dy是函数在点A的切线对应△x在纵坐标上的增量，当|△x|取值足够小时，|△y-dy|要比|△y|得多（高阶无穷小），因此在点 A 附近，就可以用切线段拉近似替代函数曲线。

从简单直观的角度来看，微分思想指的是：如果函数在足够小的范围内，可以用其他的线性函数来表示的话，那么函数在这个足够小的范围内的函数图形就可以近似看作成一段直线。通过微分能够使线性函数的数值计算结果座位原函数的数值近似值，这就是运用微分方法进行近似计算的基本思想。可以说，借助微分的近似代替，使对复杂函数的研究在局部上得到了简化。

1.2 积分的基本思想

微分是对函数的求导运算，而积分则可以看作是微分的逆运算，即他它是在得知函数的导函数的基础之上求解原函数的过程，积分分为不定积分和定积分两个基本类别。

1.2.1 不定积分：假设 F（x）是函数 f（x）的一个原函数，则函数f（x）对应的所有原函数则为F（x）+C（C 为任意常数），这个式子叫做f（x）的不定积分，求解原函数的过程，即为积分的过程，记作为：∫f（x）dx=F（x）+C。

1.2.2 定积分：假设实函数在区间［a，b］上连续可积，则其定积分可以表示为：，如果在区间［a，b］，函数 f（x）始终取值为正的话，那么可以将函数在这一区间上的定积分看作是：在坐标平面上，由（x，f（x））所构成的曲线与x轴，以及x=a和x=b这两直线所围成的面积。

2 微积分思想在经济学中的重要性

在经济学众多问题的分析中，微积分都扮演着重要的工具角色。微积分通过分析求解变量的变化规律，来使经济学问题的研究更为地简化，它不仅使经济学的研究范围变得更宽扩，还为经济学研究提供了深刻的思考方式和科学的分析方法，在当前分析经济问题研究中发挥出来愈来愈重要的作用。

2.1 拓宽了经济学的研究范围

经济学是一门讲求实践性的学科，研究的内容十分丰富。然而，任何学科的研究只有在其特定的领域中运用特定的方法才能依据实际情况或者假设条件得出准确的结论，超出这一范围，便会影响结论的准确性和科学性。在以往大多数经济学问题中，大多是从经济学特有的研究视角出发去研究，缺乏学科交叉性，由此得出的解决和作出的决策存在一定的局限性，而将微积分的理论引入到经济学之中，不仅会使经济学的研究范围得到有效拓宽，也能够借助数学工具，与其他学科建立起研究桥梁，实现更加深层次地交叉研究，进而通过微积分的分析来把握经济活动的本质和规律。

2.2 为经济学提供了科学的分析方法

在经济学中，常常需要为企业分析资源最佳资源配置、经济效益最大化等问题，在过去，大多依靠企业管理者凭借个人经验作出选择。而随着微积分思想与经济学的交叉发展，经济学中的这些问题都可以转化为相应的数学问题。例如，在经济学的最优化问题中，从经济学角度相当于经济活动偏离“顶峰”位置时，所获得的效益就会下降，而将一问题转化为微积分的问题后，就满足了费马定理的运用条件，即可以将“顶峰”位置作为极值点，在其上的导数为零，这样就可以顺利的求解。

2.3 使经济学中的决策更加严谨和准确

经济学的主要研究内容是帮助经济体或者组织实现资源优化配置和社会效益最优化，其研究的对象常常涉及经济制度、宏观政策、社会心理和人们的价值观念等等，但作为社会科学的经济学，很难将这些研究对象进行抽象量化进而分析，而数学工具的引入，则可以为社会科学的问题分析带来科学的模型和严谨的计算公式。微积分作为重要的数学工具，可以确保经济问题在计算分析过程中的更加地严谨，得出的结论也更加地准确，从而使经济学的研究更加全面和深入。

3 微积分思想在经济学中的应用实例

随着社会的发展，在经济领域中所出现的问题也呈现出了多样化和复杂化的发展趋势，由此给经济学的研究带来更多的挑战，因此，将微积分思想更深入和广泛地运用于经济学问题的定量分析十分地必要，这不仅能够为经济主体的企业经营者提供客观、精确的数据，为企业经营者科学决策提供量化依据，还能够促进经济学理论的不断发展。具体来说，在经济学中，微积分思想被应用于许多方面问题的分析求解，下面，本文将以几个典型的应用实例，来谈谈微积分思想在经济中的应用。

3.1 微分思想在利润最大化问题中的应用

在微分学中，通过对已知的函数进行求导后，就可以得到原函数的导数，即边际函数。而在经济学之中，边际概念是十分重要的经济学命题之一，通常在经济学中表示经济变量的变化率。在微观经济学中的理论认为，当经济主体的产量接近或等于边际收入和边际成本时，企业这时所能获得的利润为最大。在实际的企业中，企业的管理者常常通过确定边际成本进而来确定所需资料的成本决策。而利用微分的思想，即可将企业确定生产量而实现利润最大化的问题转化为微分方程计算，使问题得到简化。

例：某生活用品生产企业的生产成本C和产量Q之间的函数关系为C（Q）=2Q+100（元），企业的收入R与产量Q函数的函数关系为R（Q）=262Q-Q2（元）。 试问，当企业生产多少件产品时，企业的利润L（Q）能够达到最大？

对于这个问题，可运用微分的思想来求解：

L（Q）＝R（Q）-C（Q）＝260Q-Q2-100

令 L'（Q）＝0，得 Q＝130（件）

验证：由于 L″（Q）＝-2＜0，所以当生产 130 件时，企业将获得最大利润，为16800元。

3.2 积分思想在利润最大化问题中的应用

如前文所述，积分是微分的逆运算，而在经济学中，积分思想大多应用于通过已知函数积分来求解原函数。在如今经济学与社会学交叉融合发展的趋势下，诸如存款贷款问题、医疗保险问题、金融利率等问题都需要利用积分思想来进行分析和求解，积分思想的重要性越来越凸显出来。

例：某企业生产一款产品的边际收入函数为R'（x）=9-x（万元/吨），固定成本为 1 万元，边际成本函数为（万元/吨），求企业取得最大利润时的产量和利润分别是多少？

由上述分析可以得出，企业的总收入函数为：

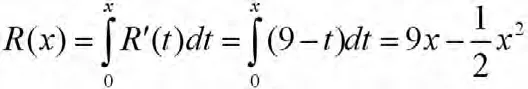
企业的总成本函数为：

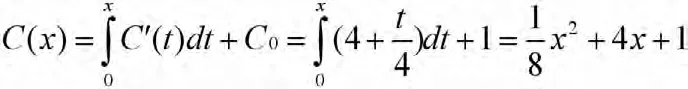
所以企业产量为4时，企业获得最大利润9万元。

4 结语

在当今的学科交叉研究越来越深入的趋势下，微积分思想与经济学的研究也更加紧密地结合了起来，当前，微积分在经济学领域中的应用还有很多的实例，通过微积分思想的引入，不仅将经济学问题转化为了量化的数学问题，使的问题的求解过程更加简单，同时还为经济学问题的研究有了全新的视角，拓宽了经济学的研究领域。当然，在本文中，仅是对微积分思想进行了简单的介绍，并对经济学中两个典型的实例进行了解析，在现实的生活中，这类的问题还有很多，本文仅是简单地介绍，希望通过本文的研究能够帮助人们了解微积分思想在经济学中的重要作用，并且希望通过本文的研究能够促进微积分思想在更多的学科中得到更广泛而深入地应用。

［1］赵军健.微积分在经济学中应用教学探索及实例研究[J].科技风,2014(16).

［2］于河.浅谈微积分在经济分析中的应用[J].辽宁对外经贸学院,2014(20).

［3］梁海滨.微积分知识在生活中的应用[J].辽宁对外经贸学院,2013(30).