轮胎侧偏刚度有限元仿真研究

姜明磊，周 涛，叶树斌，臧孟炎

(1.华南理工大学机械与汽车工程学院，广东 广州 510640)

(2.广州市华南橡胶轮胎有限公司，广东 番禺 511486)



轮胎侧偏刚度有限元仿真研究

姜明磊1，周 涛2，叶树斌1，臧孟炎1

(1.华南理工大学机械与汽车工程学院，广东 广州 510640)

(2.广州市华南橡胶轮胎有限公司，广东 番禺 511486)

以某半钢子午线轮胎为研究对象，建立基于有限元软件ABAQUS的复杂花纹轮胎侧偏特性分析有限元模型。基于隐式有限元方法实现轮辋安装、轮胎充气和垂向载荷加载，基于显式有限元方法分析各侧偏角轮胎侧向力的时间历程，获得该轮胎的侧偏刚度。侧偏刚度仿真结果与对应的实验结果一致，确认了仿真分析方法的有效性。在此基础上，就带束层结构、冠带层结构和三角胶硬度等参数对轮胎侧偏刚度的影响进行了仿真研究,并对仿真结果进行了实验验证。

子午线轮胎；设计参数；侧偏刚度；有限元方法

汽车的操纵稳定性在很大程度上取决于轮胎的侧偏特性，所以对轮胎侧偏特性的研究是汽车操纵稳定性研究的基础。汽车操纵稳定性的评价方法主要有主观评价法，其评价指标主要由轮胎带束层结构、冠带层宽度以及三角胶硬度等参数构成，因此研究轮胎的各项设计参数对侧偏刚度的影响并反馈至相关设计过程，可以实现优化轮胎侧偏性能的目的。

传统的实验方法当然是研究轮胎侧偏特性的重要手段[1]。近年来，随着计算机技术的迅速提高和有限元商用分析软件的不断完善，有限元仿真分析方法开始应用于轮胎侧偏特性研究工作。文献[2]以子午线光面轮胎为研究对象，仿真分析在特定侧偏角下轮胎的侧偏性能、带束层帘线角度对轮胎接地压力、接地印痕、侧向力、应变能等的影响。文献[3]使用ABAQUS的稳态传输分析方法，针对简单花纹轮胎分析了帘线角在50°～90°范围内侧偏刚度与帘线角度的相关关系。文献[4]采用有限元分析法研究冠带层模量对轿车子午线轮胎接地性能和侧向刚度的影响。文献[5]构建了非对称花纹、对称花纹以及无花纹等胎面花纹结构的轮胎有限元模型，并运用先隐式后显式的分析方法，考察了胎面花纹对轮胎侧偏特性的影响。

鉴于轮胎花纹对轮胎侧偏特性有重要影响，本文建立某复杂花纹轮胎的有限元模型，使用有限元软件ABAQUS的隐式分析方法完成轮辋安装、轮胎充气和自重加载过程，并建立不同侧偏角度的轮胎侧偏性能分析有限元模型，使用显式分析方法进行10km/h速度下轮胎侧偏特性仿真分析，并对计算结果进行处理得到该轮胎的侧偏刚度。有限元仿真结果与实验结果一致，确认仿真分析方法的有效性，在此基础上研究了带束层帘线角度、冠带宽度和三角胶硬度的改变对侧偏刚度的影响。

1 轮胎侧偏特性参数

从理论上讲，行驶时车轮的航向与车辆的行驶方向应该是相同的，但是由于设计、制造等因素的影响，尤其是轮胎内部帘线周向排布不均匀，使得轮胎在直线行驶时由于胎体的非对称性而产生侧向力，导致汽车在行驶过程中，车轮的实际行驶方向并不在它的旋转平面内，即车轮产生了侧偏现象[6]。

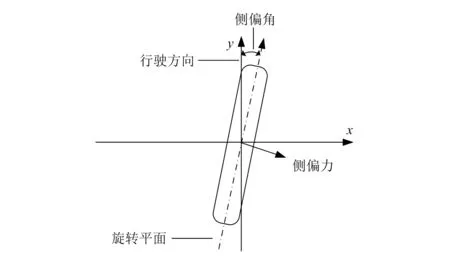
图1 车轮侧偏

图1是车轮在发生侧偏时的俯视图。车轮的旋转平面与行驶方向的夹角，称作侧偏角。此时，轮胎在接地区域发生侧向变形，所产生的垂直于车轮旋转平面的力，可以看作是车轮抵抗侧偏的反作用力，称作侧偏力。在侧偏角较小时，侧偏力等同为侧向力。

把直线行驶(侧偏角为0°)时轮胎所受的侧向力称为帘线角度效应(ply steer)，随着车轮滚动方向的不同，该侧向力方向也会改变[7-8]。发生侧偏时，侧偏力与侧偏角的关系是轮胎侧偏特性的一个重要方面，在“侧偏力-侧偏角”曲线中(见图2)，侧偏角为0°时的斜率称为侧偏刚度，记为Cα，单位是N/(°)。

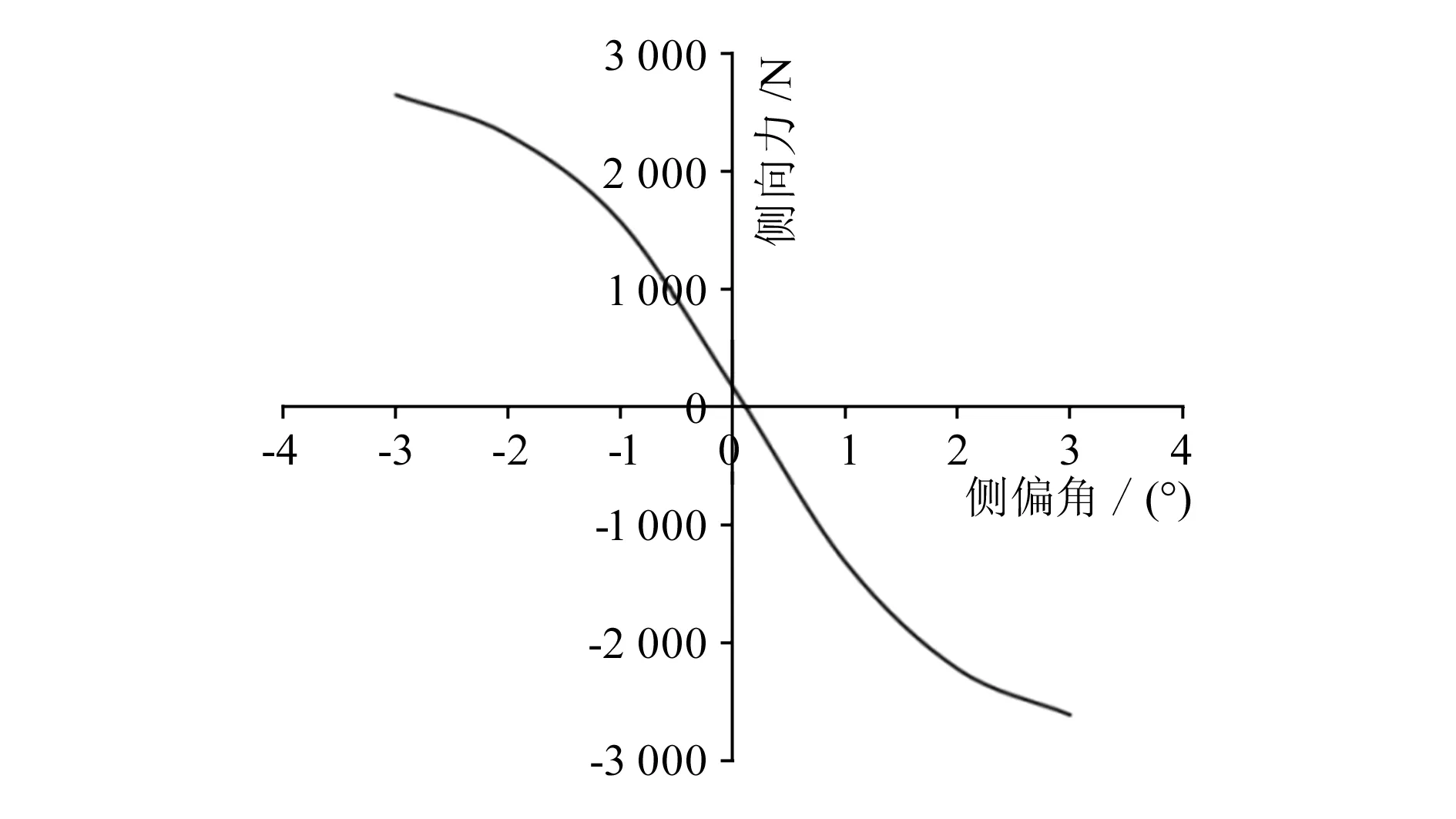
图2 侧偏力-侧偏角关系曲线

通常在小侧偏角范围内，侧偏力与侧偏角几乎呈线性关系，因此可根据式(1)，取侧偏角为1°时的侧偏力LF+1与-1°时的侧偏力LF-1的平均值作为近似的侧偏刚度[1]。

2 轮胎侧偏有限元仿真分析

基于先隐式后显式的分析方法，轮胎仿真模型的建模流程，主要包括以下两个步骤：1)有限元网格划分；2)隐式模型与显式模型的定义。建模流程如图3所示。

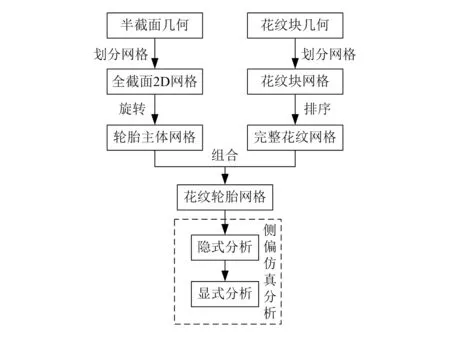
图3 轮胎有限元建模流程图

2.1 复杂花纹轮胎有限元网格模型

由图3可知，有限元网格的划分包括胎面花纹网格与轮胎主体网格两部分。首先对5节不同的花纹块几何模型进行网格划分，然后严格按照节距的排列顺序沿轮胎周向进行组合排列，得到完整的三维花纹网格[9]，如图4所示。

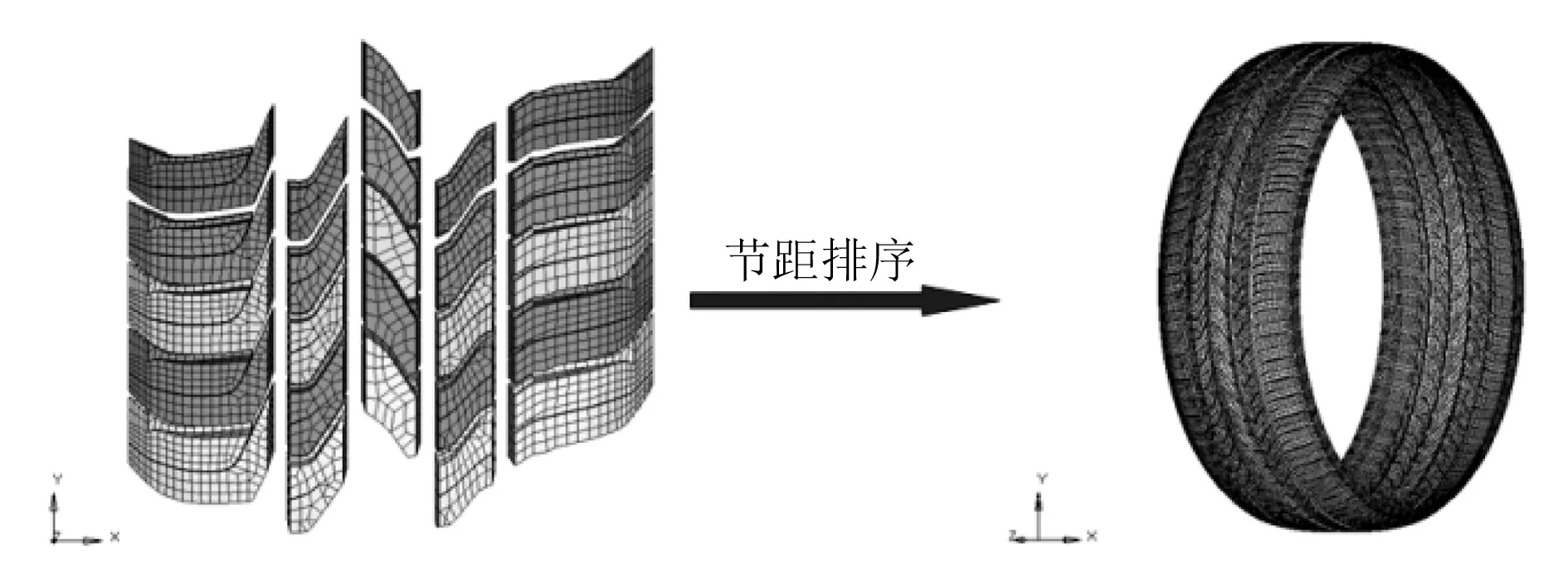
图4 胎面花纹网格组合排列

根据轮胎主体结构的周期对称性，通过旋转功能把主体的二维截面网格扩展为三维网格，最后把胎面花纹与轮胎主体进行组装，获得复杂花纹轮胎的有限元网格，如图5所示。

图5 花纹与轮胎主体的装配

2.2 轮胎材料

把轮胎有限元网格导入ABAQUS，定义轮胎材料。橡胶属于超弹性材料，其本构关系采用Yeoh模型，材料参数由相关实验结果拟合获得。

由于各层帘线材料具有拉伸模量与压缩模量不相等的材料特性，即“双线弹性”，而ABAQUS/Explicit的材料库中没有与此相对应的材料模型，因此借助Explicit用户材料子程序VUMAT[10]把“反正切帘线模型”[11-13]引入显式模型的仿真计算中，具体的材料模型表达式如式(2)所示。

式中：E为帘线的模量；ε为帘线的轴向主应变；E1为帘线的拉伸模量；E2为帘线的压缩模量，其值取为拉伸模量的1/10或1/100；ks为帘线拉压转化区域模量曲线(见图6)的曲率参数，ks值越大，曲线就越陡峭，模型就越接近于双线性弹性模型；εc为移位参数，用于判断帘线所受的拉压状态。本文直接引用文献[13]中的帘线材料参数，且取钢丝帘线的压缩模量为拉伸模量的1/10，取尼龙帘线的压缩模量为拉伸模量的1/100。

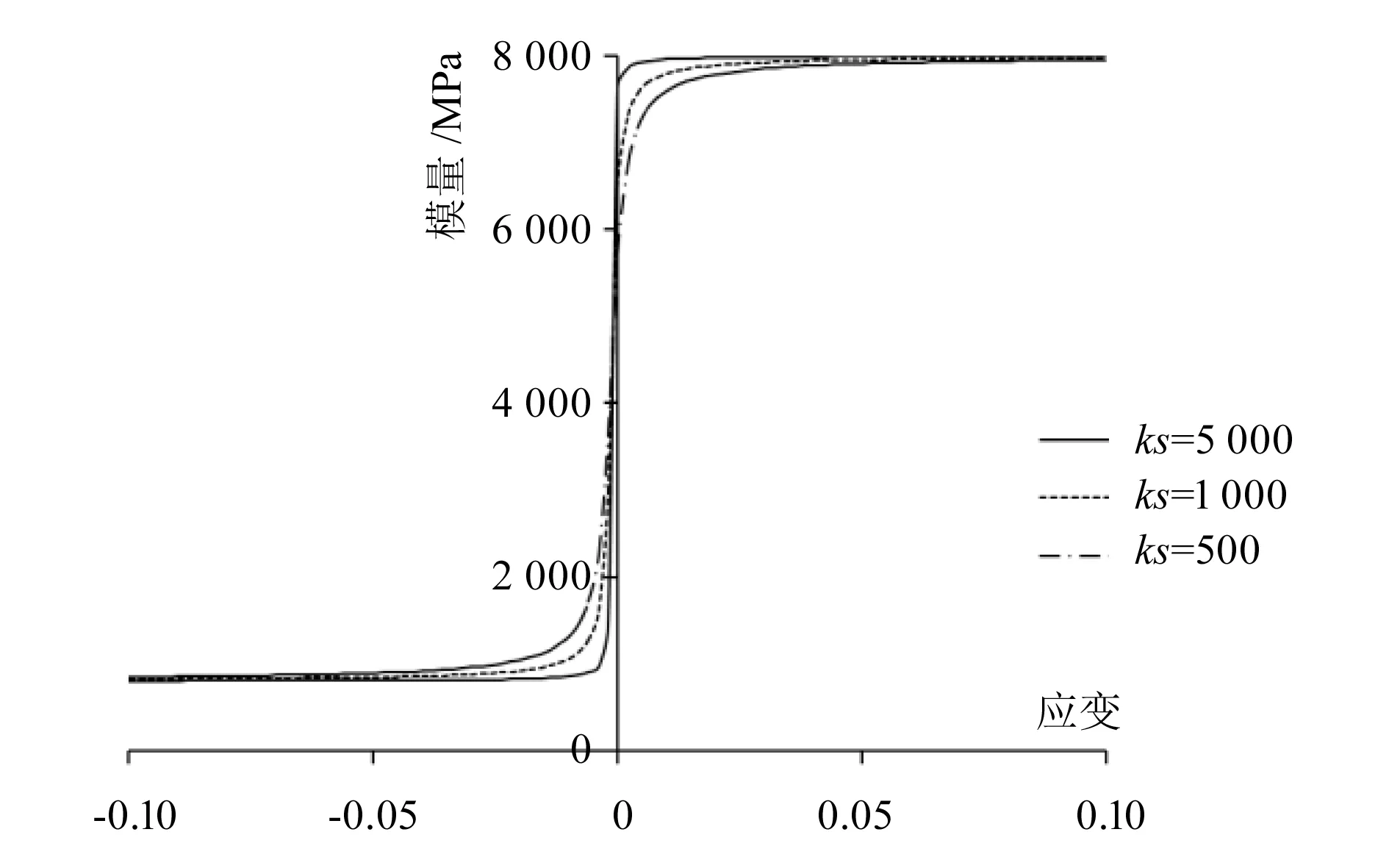
图6 双线性弹性模量曲线

2.3 轮胎侧偏有限元模型和仿真分析

本文采用隐式加显式的分析方法进行轮胎侧偏有限元仿真[14]。隐式分析过程包括：1)改变轮辋的初始位置并施加沿轴向的位移边界条件，以模拟轮辋的装配过程；2)对轮胎内衬层的内表面施加均布载荷0.2MPa，以模拟轮胎的充气过程；3)在垂直方向上对路面模型先后施加位移边界条件和集中力载荷，使其逐渐压紧轮胎，以模拟轮胎垂直载荷的加载过程。

然后使用*Import命令，利用数据传递功能把隐式计算结果作为显式分析的初始条件。在显式模型中，只释放轮辋绕旋转轴的转动自由度，同时对路面施加速度载荷，该速度与实际车速大小相等、方向相反，仿真计算得到车轮旋转的线速度为10km/h、侧偏角为-1°～1°条件下轮胎侧向力的时间历程，如图7所示。

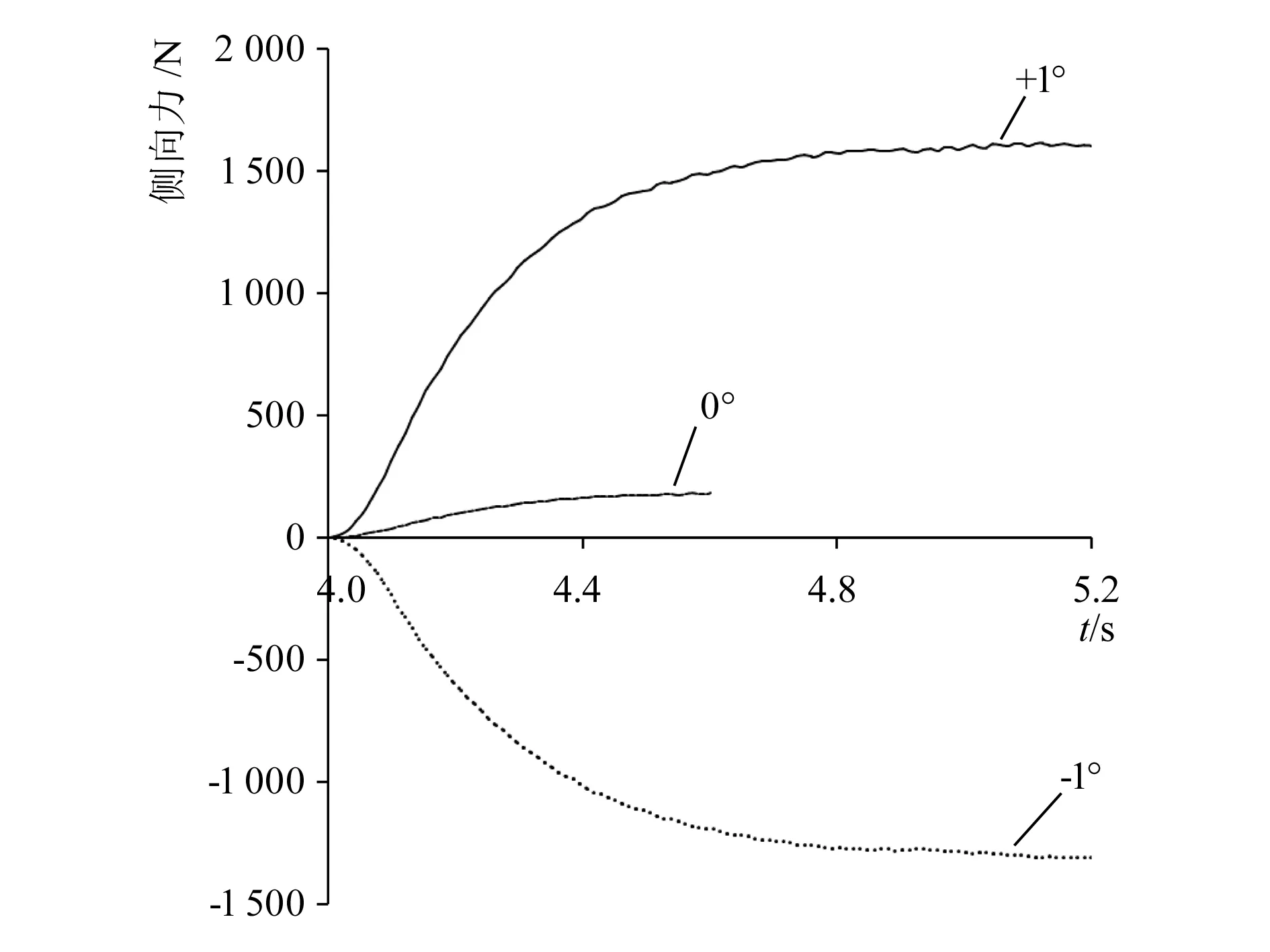
图7 轮胎侧向力的时间历程

2.4 仿真结果评价

图7中侧偏角为-1°和+1°的侧向力时间历程曲线，以其接近水平部分(5.1s～5.2s)的数据平均值作为对应侧偏角的侧向力，使用式(1)求得该轮胎的侧偏刚度仿真结果，并与相应的试验结果进行比较,见表1。

表1 侧偏刚度的仿真结果与试验结果对比

由表1可知，轮胎侧偏刚度的仿真结果与试验结果非常接近，说明了轮胎侧偏特性有限元仿真分析方法的正确性。

3 轮胎侧偏刚度影响因素分析

以前述轮胎模型为基础(设为方案1)，分别改变带束层帘线角度(方案2)、三角胶硬度(方案3)和冠带层宽度(方案4)，研究它们对轮胎侧偏刚度的影响。

分别建立方案2～方案4的轮胎侧偏有限元模型，然后进行仿真计算，获得各方案的仿真结果。各方案的轮胎侧偏刚度仿真结果与试验结果的对比情况见表2～表4。

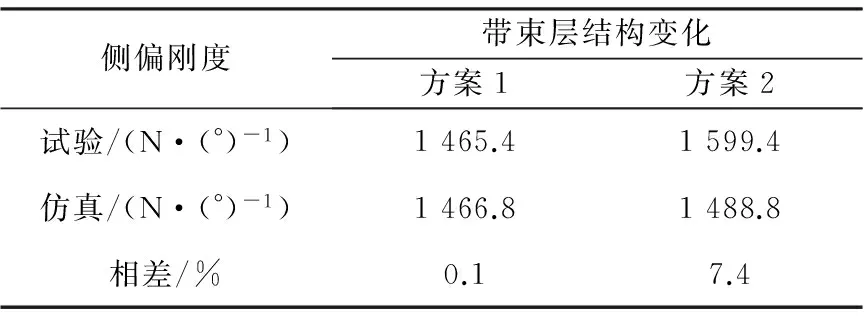
表2 带束层角度对侧偏刚度的影响

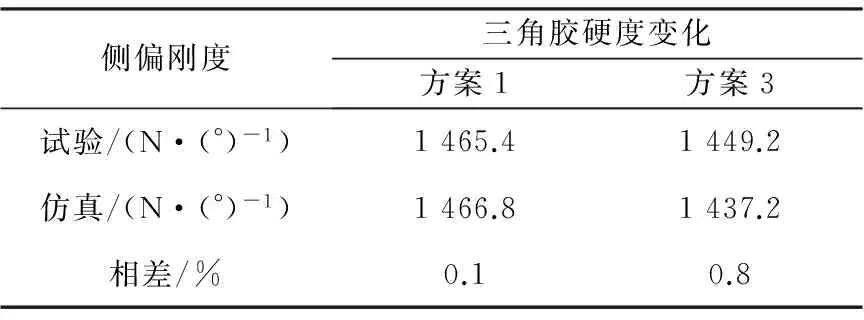
表3 三角胶硬度对侧偏刚度的影响

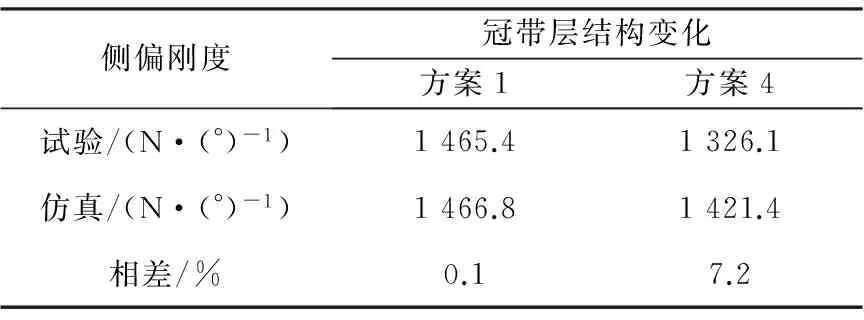
表4 冠带层结构对侧偏刚度的影响

包含方案1在内的4个轮胎侧偏刚度仿真结果与试验值相差在8%以内，进一步说明了轮胎侧偏特性有限元建模和仿真分析方法的有效性。

带束层帘线角度、三角胶硬度和冠带层宽度变化对轮胎侧偏刚度的影响如图8所示。由图8可知，改变带束层帘线角度、三角胶硬度以及冠带层宽度，轮胎侧偏刚度的仿真结果与实验结果变化趋势一致，说明有限元仿真分析方法可以在轮胎侧偏特性优化设计过程中发挥重要作用。

相对于三角胶硬度变化对侧偏刚度的影响其仿真结果与实验结果的一致性程度，带束层帘线角度和冠带层宽度的变化对侧偏刚度仿真结果的影响明显小于实验。造成这种现象的原因可能是由于帘线材料参数未能使用实验轮胎相应的材料参数所致，有待进一步的研究。

4 结束语

本文以某复杂花纹半钢子午线轮胎为研究对象，采用隐式加显式的有限元分析方法得到了与实验结果非常接近的侧偏刚度。然后，改变该轮胎的帘线角度、三角胶硬度和冠带层宽度，仿真分析了它们对轮胎侧偏刚度的影响，所得结果显示，其变化趋势与实验结果的变化趋势一致，说明有限元仿真分析方法可以在轮胎侧偏特性的优化设计过程中发挥作用。

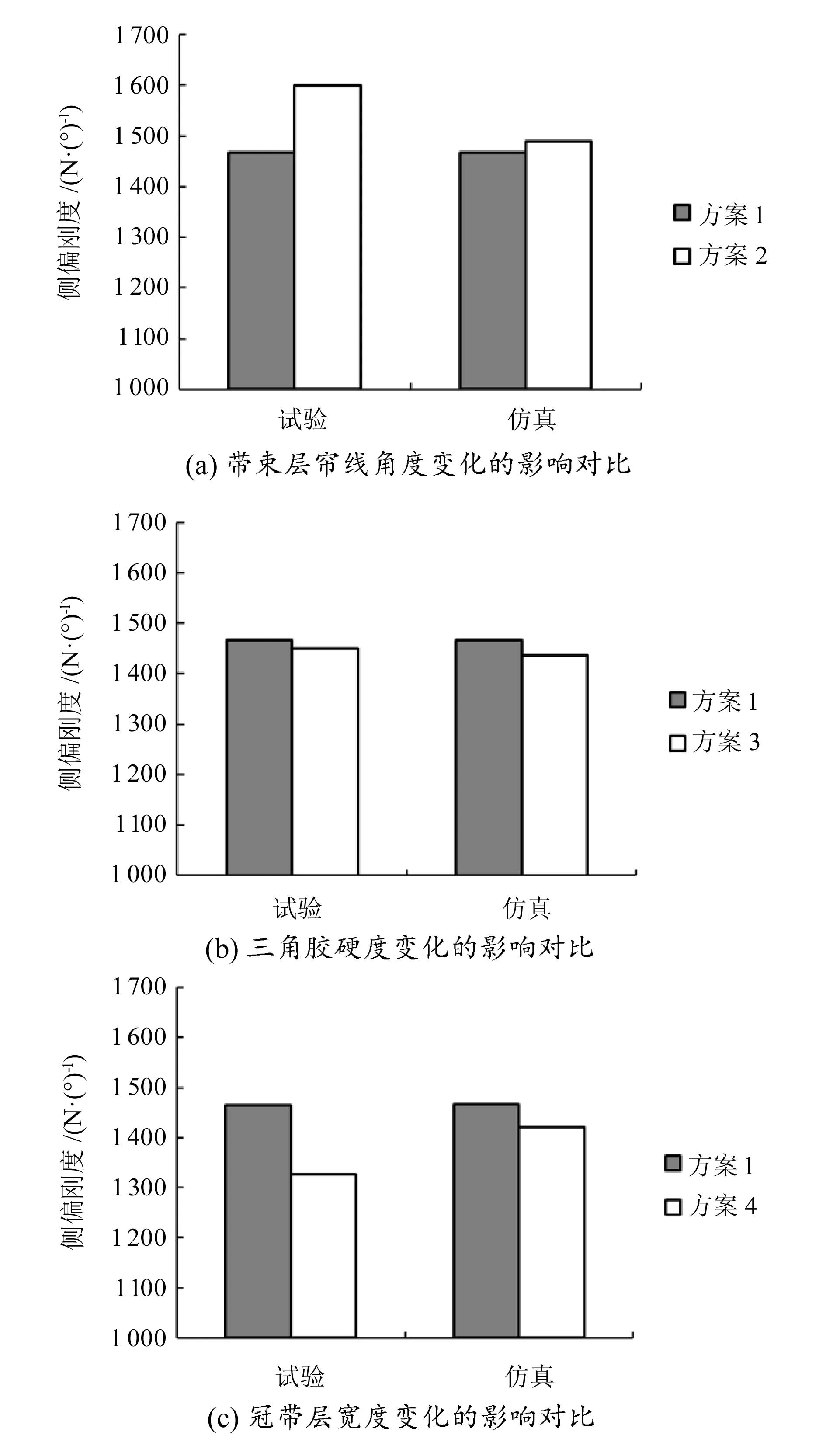
图8 侧偏刚度的仿真与实验的趋势对比

但是，全面描述轮胎侧偏特性还包括残余回正力矩和残余侧向力。由于委托实验结果离散性过大，文中未做讨论。另外，本文中轮胎钢丝和尼龙帘线的材料物性直接采用了参考文献的数值，可能是导致帘线角度和冠带层宽度变化对侧偏刚度的影响不如实验结果敏感的原因。今后，将加强实验研究力度，使有限元仿真分析方法更有效地服务于轮胎设计过程。

[1] 黄舸舸，蒋中凯，危银涛，等. 带束层结构对载重子午线轮胎侧偏特性的影响[J]. 轮胎工业，2011, 31(7): 394-398.

[2] Ghoreishy M H R. Finite element analysis of steady rolling tyre with slip angle: effect of belt angle [J]. Plastics, Rubber and Composites, 2006, 35(2): 83-90.

[3] Lu Min. FEA study of belt angle effect to cornering stiffness and ply steer [C]//ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. San Diego, USA: ASME,2009: 703-705.

[4] 区志明，王友善，汪俊. 冠带层模量对轿车子午线轮胎接地性能和侧向刚度的影响[J]. 轮胎工业，2010, 30(8): 459-462.[5] 曾光，李子然，夏源明. 计及胎面花纹影响的轮胎侧偏特性有限元分析[J]. 中国科学技术大学学报，2013, 43(6):497-502.

[6] Gent A N, Walter J D. 轮胎理论与技术[M]. 危银涛， 李勇，冯希金，译. 北京：清华大学出版社，2013.

[7] Matyja F E. Steering pull and residual aligning torque [J]. Tire Science and Technology, TSTCA, 1987, 15(3): 207-240.

[8] Pottinger M. Tire/Vehicle pull: an introduction emphasizing plysteer effects [J]. Tire Science and Technology, TSTCA, 1990, 18(3): 170-190.[9] 徐文冰. 基于有限元方法的轮胎磨损特性研究[D]. 广州：华南理工大学，2013.

[10] Simulia Software Corporation.Abaqus User Subroutines Reference Manual [M]. Providence: Simulia Software Corporation, 2010.

[11] 李炜. 子午线轮胎结构有限元分析和设计原理的若干问题研究[D]．合肥：中国科学技术大学，2003.

[12] 李兵. 计及复杂胎面花纹的子午线轮胎结构有限元分析[D]. 合肥：中国科学技术大学，2008.

[13] 李钊. 轮胎胎面磨耗行为的实验研究与数值分析[D]. 合肥：中国科学技术大学，2013.

[14] Li Zhao, Li Ziran, Xia Yuanming. An implicit to explicit FEA solving of tire F&M with detailed tread blocks [J]. Tire Science and Technology, TSTCA, 2012, 40(2): 83-107.

Research on cornering stiffness based on FEM

JIANG Minglei1, ZHOU Tao2, YE Shubin1, ZANG Mengyan1

(1.School of Mechanical and Automotive Engineering, South China University of Technology, Guangdong Guangzhou, 510640, China)

(2.South China Tire and Rubber Co., Ltd., Guangdong Panyu, 511486, China)

Based on one type of PCR tire, it builds the finite element models of treaded tire to investigate on the cornering properties in ABAQUS. The tire analysis is divided into two steps: implicit analysis and explicit analysis. The implicit analysis consists of the mounting, inflating and vertical loading. Subsequently, the time history of lateral force at varied slip angles is performed in the explicit analysis and then the cornering stiffness is obtained. The simulation results are consistent with the experimental ones, which confirm the validity of the proposed method. At last, it takes the simulations and experiments on the belt structure, the cap ply structure and the hardness of bead filler, shows that above items affect the tire cornering stiffness.

radial tire; design parameter; cornering stiffness; FEM

10.3969/j.issn.2095-509X.2015.09.005

2015-06-19

国际科技合作项目(2013DFG60080)

姜明磊(1990—)，男，山东烟台人，华南理工大学硕士研究生，主要从事汽车CAE方向的研究。

U463.341

A

2095-509X(2015)09-0015-05