差动式微力加载装置的结构设计与优化

龙 灿，王 勇

(合肥工业大学机械与汽车工程学院，安徽 合肥 230009)



差动式微力加载装置的结构设计与优化

龙 灿，王 勇

(合肥工业大学机械与汽车工程学院，安徽 合肥 230009)

为了在微力标定系统中实现微力稳定加载，设计了一种基于柔性铰链的等厚度对称差动式垂直微力加载装置。首先对装置的工作原理以及平衡性做了详细介绍；然后在对装置结构参数进行单因素分析后，选取一组参数进行正交试验及极差分析，得出结构参数对输出微力影响的主次关系和装置的较优参数组合；最后，对优化后的模型进行不同载荷分析，结果表明优化后的微力加载装置能够稳定地加载微力且具有良好的线性关系。

微力加载；微力标定；有限元分析；垂直微力

随着现代科学技术的高速发展，微力传感器在纳米技术、生物技术、精密机械工程和微机电系统(MEMS)等方面得到越来越广泛的应用[1]。虽然传统力传感器的标定方法成熟，操作简单，但对于所需标定力值很小的高精度微力传感器，尤其是标定所需力的量级要求是10-9～10-6N的微力传感器[2]，传统标定方法则不再适用。国内外现有的几种微力加载装置都无法稳定地加载微力。例如，砝码滑轮式[3]产生的微力受滑轮本身的摩擦、滑轮和细线之间的摩擦影响很大；安培力式[4]和通电线圈式[5]，易受地磁场及环境因素的影响且操作复杂；气体动态标定法[6]必须在真空环境中使用且过程敏感；悬臂梁变形式[7]方法操作要求高，且探针与悬臂梁的对准困难。微力的稳定加载已成为微力传感器标定的一大难点，因此设计一种能够稳定加载的微力加载装置是当下所迫切需要的。

1 微力加载装置的工作原理

新设计的垂直微力加载装置利用柔性铰链[8-9]传递力和位移，运用二级杠杆机构缩小在两输入端施加的差值砝码力，通过改变两输入端的砝码差值调节输出微力的大小；柔性铰链用于消除摩擦力影响，保证输出微力的稳定。

图1所示为装置的原理示意图，在装置左右两端输入差值砝码力F1和F2，利用二级杠杆机构缩小差值砝码力。根据杠杆原理(动力×动力臂=阻力×阻力臂)可得：

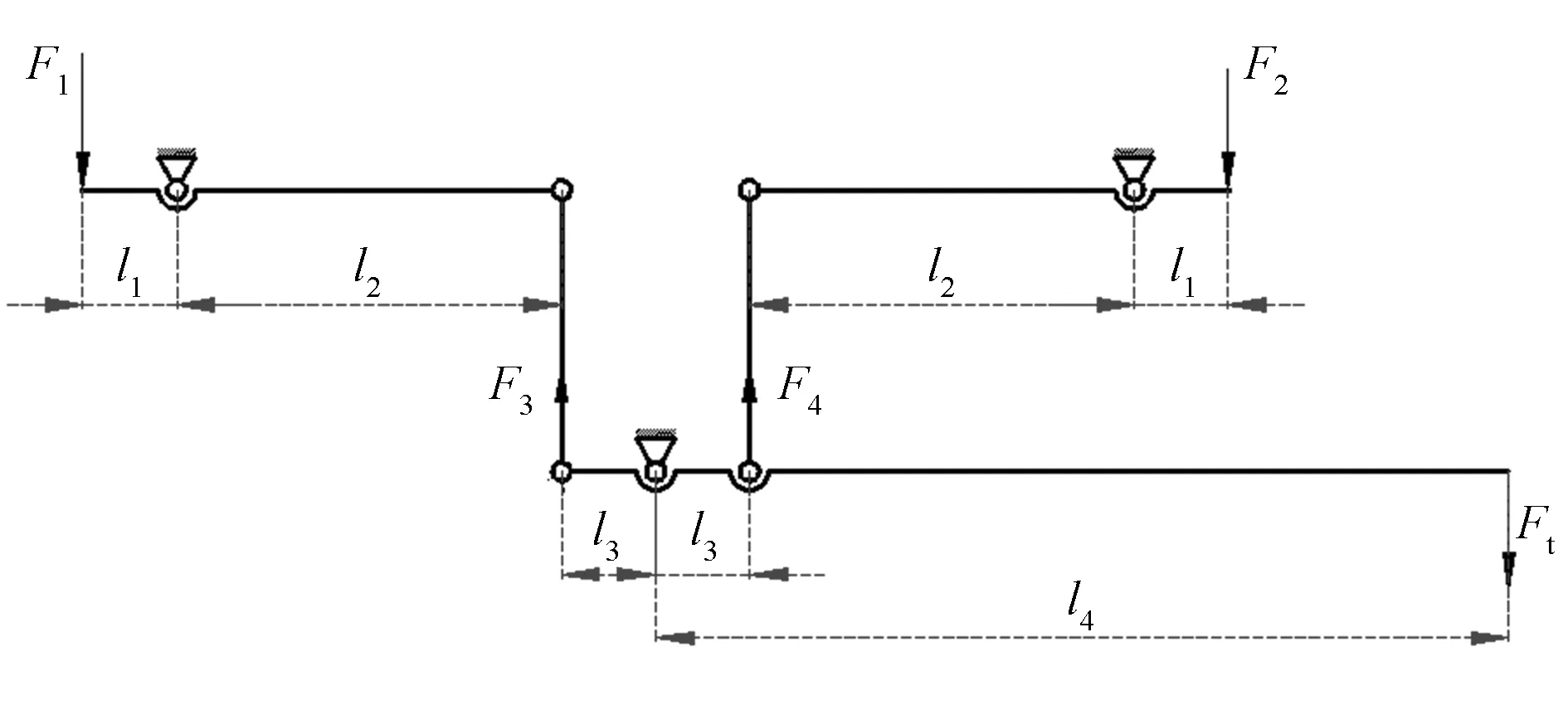
图1 微力加载装置的示意图

所以装置的力缩小倍数为

装置连杆选定为：l1=15mm，l2=108mm，l3=9mm，l4=225mm。忽略能量损耗，根据公式(4)可得理论上的力缩小倍数为

2 微力加载装置分析

目前常用的柔性铰链有倒圆角直梁形、圆弧形、椭圆形等。在这常用的3种柔性铰链中，圆弧型铰链转动精度最高，其次是椭圆形铰链，最后是倒圆角直梁形。在微力加载装置中，由于作用的力值很小，应采用具有较高转动精度的圆弧型铰链。

2.1 装置重力场下平衡性分析

微力加载装置受自身重力影响较大，为避免装置变形量过大而导致柔性铰链失效，需要对装置平衡性进行设计。在重力场下分别对装置有无配重块的两种情况进行有限元分析。装置材料选用密度小、强度较高、耐腐蚀性较好的硬铝合金2A12，其屈服极限为265MPa、抗拉强度为410MPa、弹性模量为72GPa、泊松比为0.33、密度为2.7g/cm3。定义单元类型为solid185。两种情况下装置的变形结果如图2,3所示。

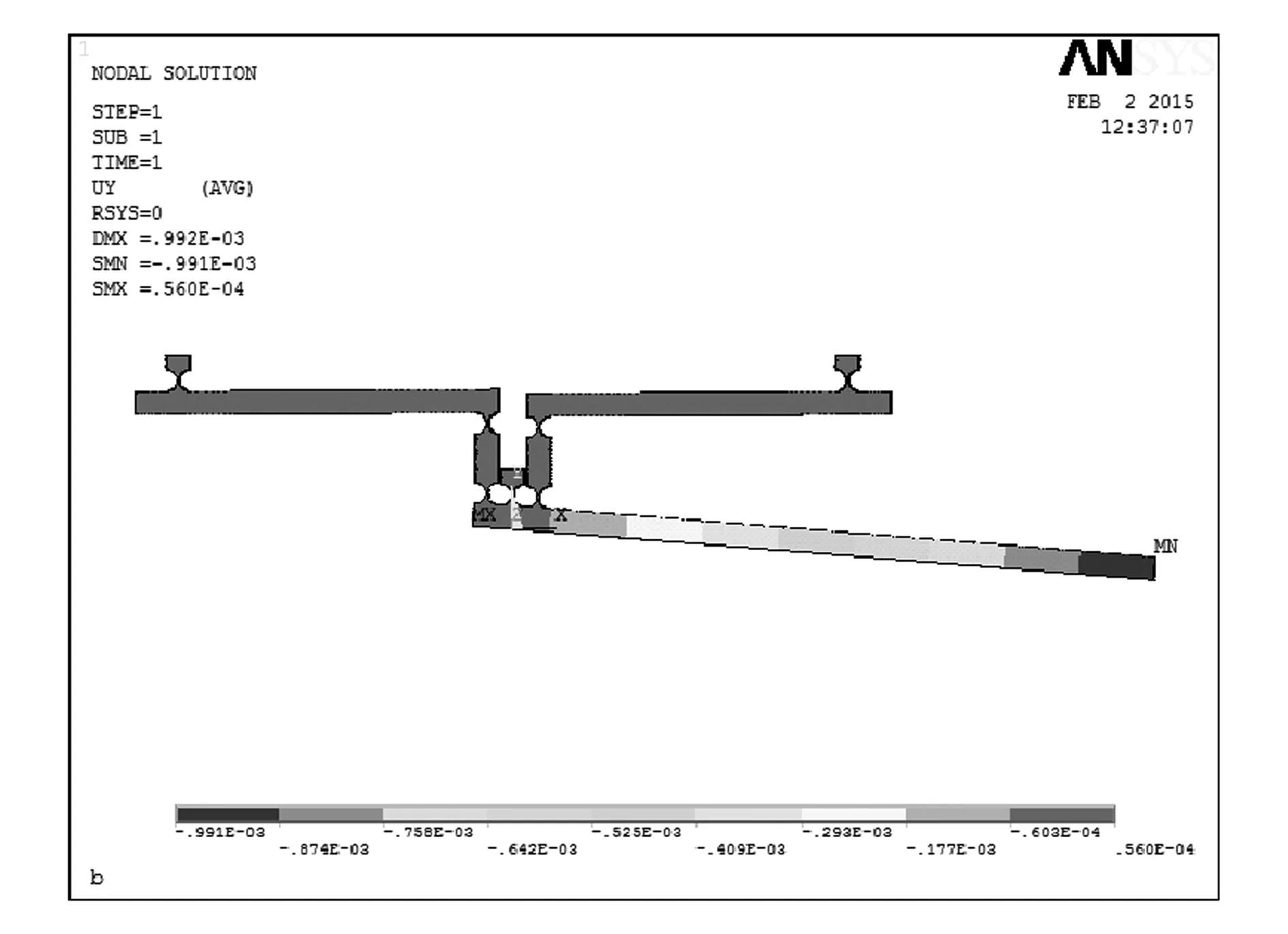
图2 无配重时装置的变形云图

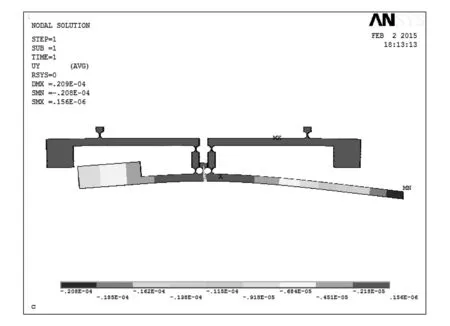
图3 有配重时装置的变形云图

不添加配重块时，微力加载装置在重力场下输出端变形量为0.991mm。利用配重块调整杠杆的平衡后，微力加载装置在重力场下输出端变形量为0.208mm。两者相比，后者的输出端变形量减少了79%，可见通过添加配重块能有效地消除装置自身重力对输出端变形量的影响。

2.2 微力加载装置的结构

微力加载装置的结构示意图如图4所示，装置中所有的转动副都采用柔性铰链；m1，m2为平衡质量，用于减小杠杆自身重力对装置变形的影响；最顶部4个螺纹孔用于固定。输出端F在竖直方向与微力传感器输入端接触，通过在2个V形槽上施加2个质量不等的圆柱体砝码，缩小砝码差值力[10]，从而实现对微力传感器的加载，以达到微力标定的目的。

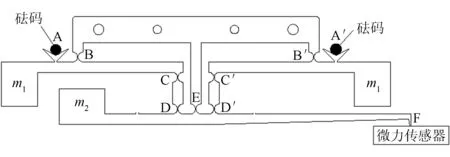
图4 微力加载装置的结构示意图

2.3 初始模型的静力学分析

微力加载装置的三维模型如图5所示，其在不同载荷下的仿真分析结果见表1。

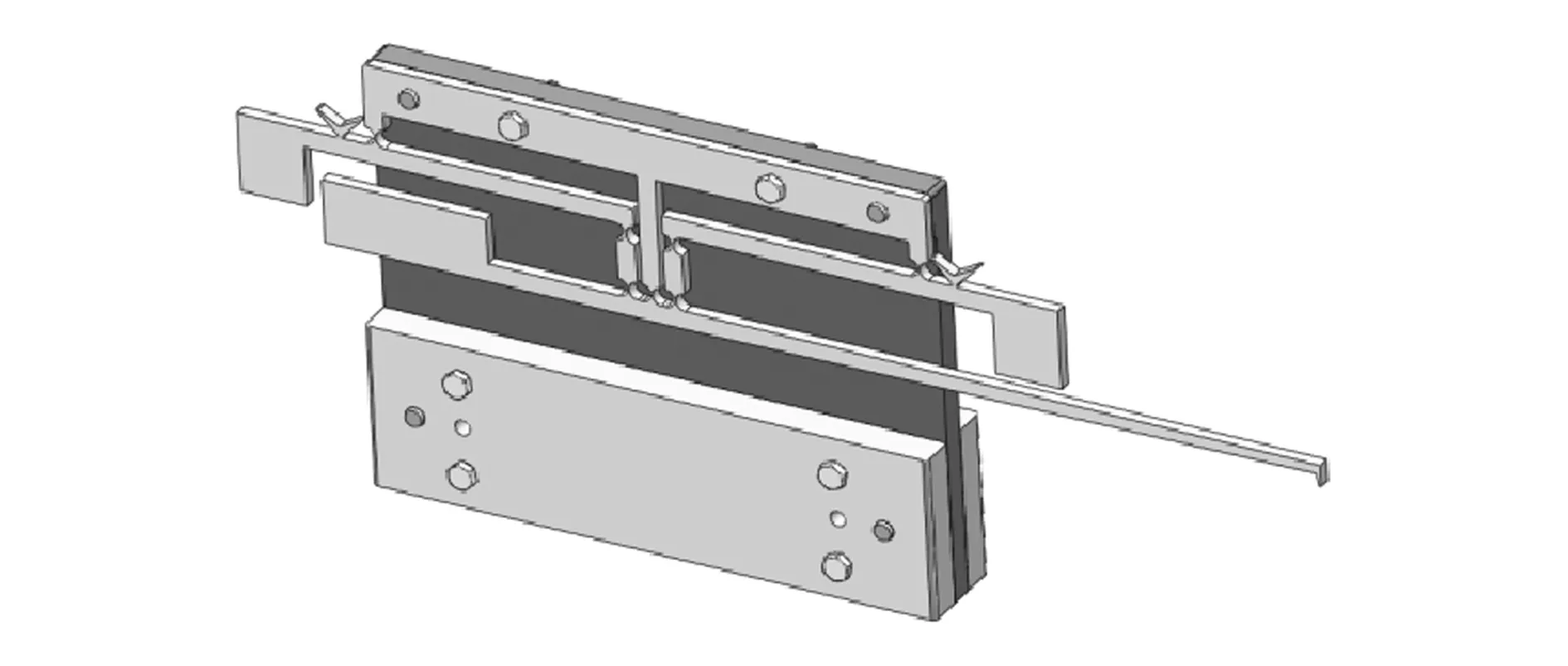
图5 微力加载装置的三维模型

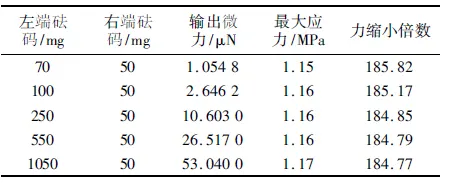
表1 不同输入载荷下的分析结果

由表1可知，输出微力与输入载荷基本上呈一种线性关系，且最大应力仅为1.17MPa，远远小于装置材料的许用应力410MPa，因此在后面的分析中可不考虑应力的影响。装置的力缩小倍数稍微大于理论值K0，这是因为装置在工作过程中存在能量损耗，使输出微力Ft小于理论值而造成的。因此，需对装置的结构进行优化以减少能量损耗。

3 微力加载装置的优化

微力加载装置是依靠柔性铰链的弹性变形来工作的，而装置的弹性变形过程中存在着能量的损耗。弹性变形主要集中在柔性铰链和中间连接杆。因此选取中间连接杆长lCD、装置厚度t和柔性铰链最小宽度(铰链分为固定铰链最小宽度b1和连接铰链最小宽度b2)作为优化的结构参数。

由于参数lCD,t,b1,b2的变化范围较大，若直接进行正交试验优化[11]，计算量很大，且很可能存在很多无用参数组合。为了能在较大范围内寻找最优结构参数，同时减少计算量，可分别对每个结构参数进行单因素分析，即分别讨论参数lCD,t,b1,b2对输出微力的影响，根据对应的参数曲线，在每个参数中选取一组较优数据，由这些数据再进行正交试验，得出装置的最优参数组合。

3.1 结构参数的单因素分析

材料不变、约束条件不变、左端施加10 290μN、右端施加490μN载荷的情况下，参数lCD,t,b1,b2在一定范围内变化，对应的输出微力的变化曲线如图6所示。

左端施加10 290μN、右端施加490μN时，输出微力的理论值应为54.444μN。由图6中4条曲线可知，装置的4个关键结构参数都表现为一种单调递减关系，其结构参数越小，输出微力越接近于理论值，但结构参数越小，装置的抗弯矩能力会降低，加工的尺寸误差也会增大。

为降低结构参数波动对输出微力的影响，应在4条曲线变化较平稳的区域选取一组数据。因此，lCD选取35，40，45mm；t选取4，5，6mm；b1选取0.2，0.3，0.4mm；b2选取0.2，0.3，0.4mm。

3.2 正交试验设计

当微力加载装置两输入端施加一组相同的差值砝码时，工作时的能量损耗越小，则输出微力就越大，所以本次试验的指标是装置的输出微力大小。

选取输出微力Ft为试验指标，连接杆长度lCD、装置厚度t、固定铰链最小宽度b1、最小连接铰链宽度b2为4个因素。每个因素的水平为：连接杆长度A1=35、A2=40、A3=45mm；装置厚度B1=4、B2=5、B3=6mm；固定铰链最小宽度C1=0.2、C2=0.3、C3=0.4mm；连接铰链最小宽度D1=0.2、D2=0.3、D3=0.4mm。

3.3 正交试验及极差分析

根据正交试验的方法，进行四因素三水平的单指标正交试验，选用L9(34)正交表进行试验，得到的试验结果数据见表2。

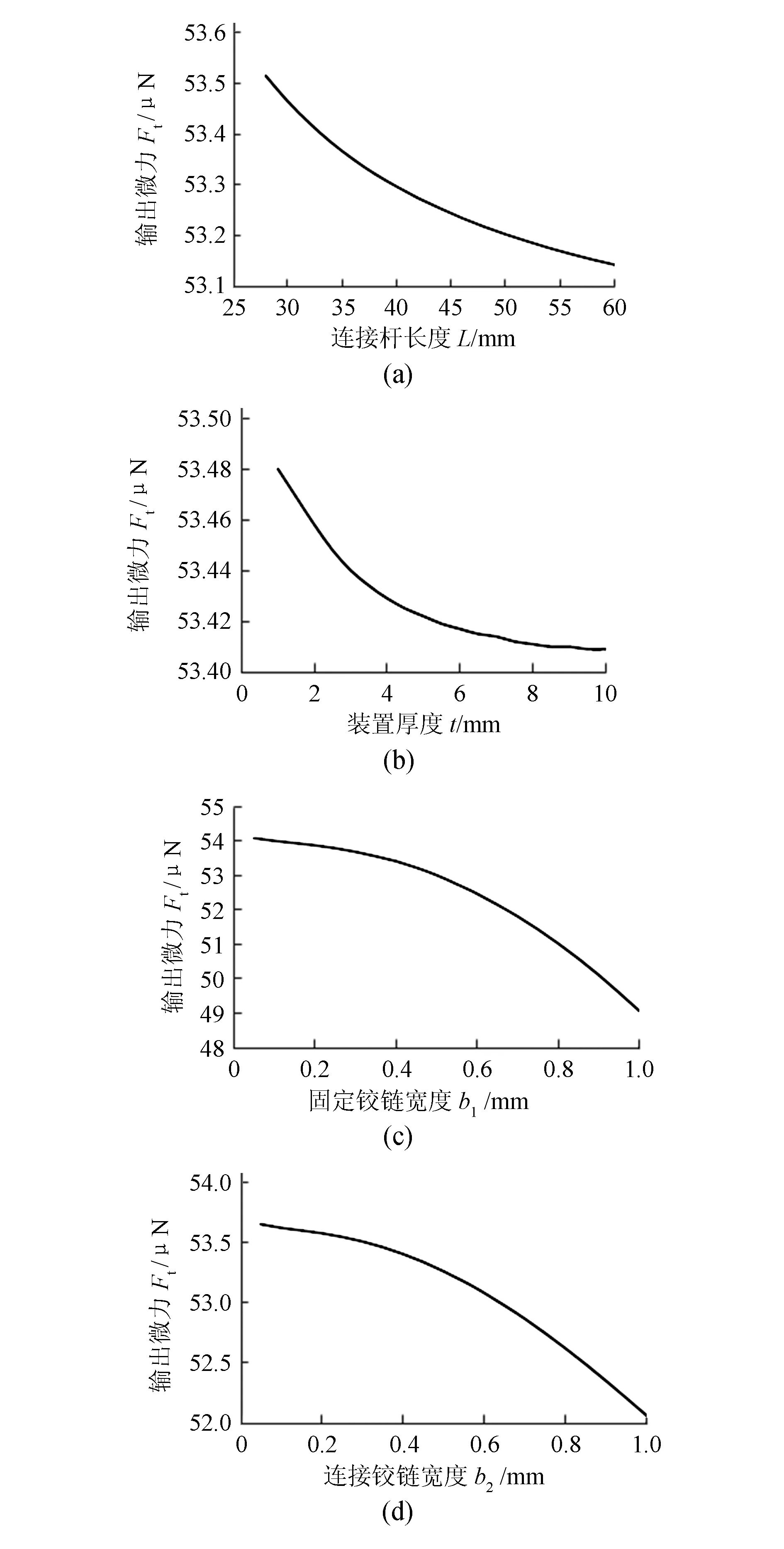
图6 结构参数与输出微力的关系

对试验的结果数据运用极差分析法进行分析，得到的极差值见表3。根据极差值R的大小可以确定出各个因素对试验指标的影响程度大小。

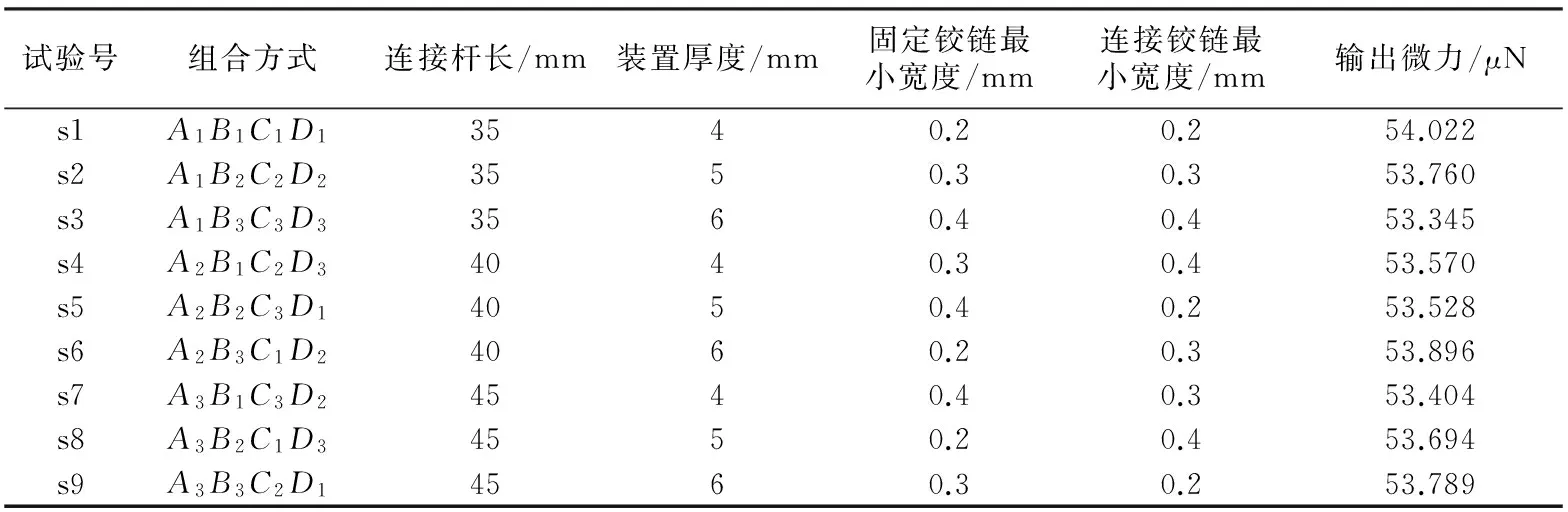
表2 正交试验表

表3 极差分析表

注：si对应正交表中试验号为si的试验结果，i=1，2，…，9。

由表3可知，各因素的主次顺序依次为：b1→b2→lCD→t，且得到最佳的组合方式A1B3C1D1，即lCD=35mm、t=6mm、b1=0.2mm、b2=0.2mm。

4 优化后的装置分析

按照最佳组合A1B3C1D1重新建立模型，对新模型施加不同载荷，进行有限元分析，分析结果见表4。

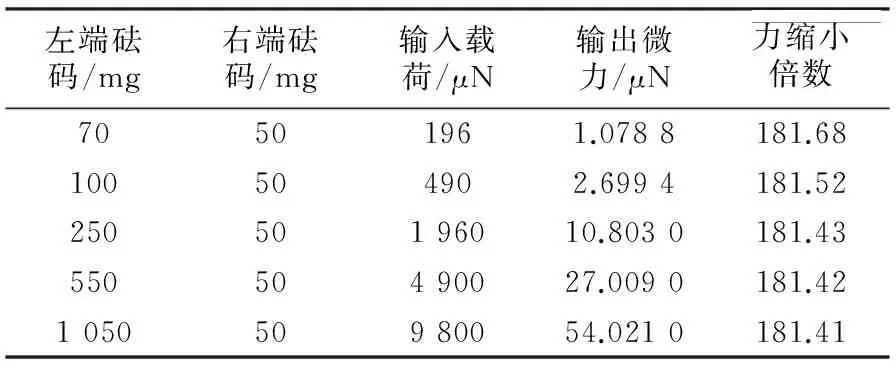
表4 优化后的装置分析结果

对比表1和表4可知，优化后的装置输出微力更加接近于理论值，且输入与输出之间有着较好的线性关系，这些都证明了此次优化有效地减少了装置在工作过程中的能量损耗。

5 结束语

本文设计的垂直微力加载装置，以柔性铰链代替传统铰链，利用二级杠杆原理缩小现有的差值砝码力；并运用正交试验方法对装置的结构进行了优化，最终的分析结果表明装置可以实现10-6～10-4μN的微小力的稳定加载。此设计为微力的稳定加载提供了一种新方法，且结构简单，操作方便，可为各种需要微力加载的系统提供技术支持，有着良好的发展前景。

[1] 牛亚楠．微力测量系统的设计制造及其实验研究[D]．长春：吉林大学，2014.

[2] 吴昌庆．微力标定与测量装置的若干关键问题研究[D]．合肥：合肥工业大学，2012.

[3] 郑红梅，刘正士，王勇．机器人六维腕力传感器标定方法和标定装置的研究[J]. 计量学报，2005(1)：43-45.

[4] Jin Wenlin，Mote C D Jr．On the calibration of multicomponent micro-force sensors[J]．Journal of Micro-electromechanical Systems，1998，7(2)：156-163.

[5] 郭琪，邹志纯．三种提供微力装置的模型[J]．西安邮电学院学报，2009(1)：149-152.

[6] Jamision A J，Ketsdever A D，Muntz E P．Gas dynamic calibration of a nano-Newton thrust stand[J]．Review of Scientific Instruments，2002，73(10)：3629- 3637.

[7] Liu Mengwei，Li Junhong，Ma Jun，et al．Design and fabrication of a MEMS Lamb wave device based on ZnO thin film[J]．Journal of Semiconductors，2011，32(4)：44-46.

[8] 崔忠炜．柔顺铰链的结构设计、仿真及实验研究[D]．北京：北京工业大学，2013.

[9] Nicolae Lobontiu．Compliance-based modeling and design of straight-axis/circular-axis flexible hinges with small out-of-plane deformations[J]．Mechanism and Machine Theory，2014，80：166-183.

[10] 郑双，高荣慧，王勇．重力场下垂直微力发生装置的研究[J]．合肥工业大学学报：自然科学版，2014(2)：134-136.

[11] 宋伟，张新，王磊．基于正交试验的应变式六维力传感器弹性体结构的优化设计[J]．工矿自动化，2009(10)：60-62.

The structure design and optimization of the differential micro-force loading device

LONG Chan,WANG Yong

(School of Mechanical and Automotive Engineering,Hefei University of Technology, Anhui Hefei, 230009, China)

In order to solve the stable load in the calibration system of micro-force, it designs a vertical micro-force loading device based on flexible hinge, which has constant thickness, symmetry and differential type. It introduces the device's working principle and balance. Based on the separately analysis of each structural parameter, it selects a set of parameters used in the orthogonal test and the extreme difference analysis, obtains the primary and secondary relationship of the structure parameters that affect the output of micro-force and relatively better parameter combinations of the structure. Finally, it analyzes the different loads of the model, provides the relatively better parameter combinations. The results show that the improved micro-force loading device can be stably loaded micro-level precision force and have a good linear relationship.

micro-force loading; calibration of micro-force; FEA; vertical micro-force

10.3969/j.issn.2095-509X.2015.09.003

2015-05-26

龙灿(1989—)，男，湖南衡阳人，合肥工业大学硕士研究生，主要研究方向为机械结构设计。

TH122

A

2095-509X(2015)09-0007-04