二阶非线性三点边值问题的解和多解性

崔艳，李群

(阜阳师范学院 数学与统计学院 ,安徽 阜阳 236000)

二阶非线性三点边值问题的解和多解性

崔艳，李群

(阜阳师范学院 数学与统计学院 ,安徽 阜阳 236000)

利用锥上的不动点定理,给出了非线性二阶三点边值问题解和多解的存在性定理,其中允许非线性项有一个负的下界.

半正非线性;存在性;多解性

1 引言及预备知识

近年来,关于非线性二阶三点边值问题的研究受到了广泛关注,取得了一些研究成果[1-5],文献[7]在非线性项满足一定增长条件下,研究了边值问题

正解的存在性,上述正解的研究大都在f非负,即f:[0,1]×[0,+∞)→[0,+∞)的情况下展开的,本文通过构造一个适用的锥,研究了边值问题(P)的解和正解的存在性和多解性,不要求非线性项f满足增长条件,并且允许非线性项f有一个负的下界,即允许f是半正的.

我们称函数ω∈C[0,1]是凹的,若ω(τt1+(1-τ)t2)≥τω(t1)+(1-τ)ω(t2),t1,t2,τ∈[0,1].

设p(t)=-ρt2+(1-αη2)t+β(1-αη2),则p″(t)=-2ρ,0≤t≤1,于是p(t)是一个[0,1]上的非负凹函数,易知p(0)=βp'(0),p(1)=αp(η),又因为

00,

直接计算表明G(t,s)满足以下性质:

定义g(t,l)=f(t,l)+M,(t,l)∈[0,1]×[-kM,+∞),g:[0,1]×[-kM,+∞)→[0,+∞)连续,考虑三点边值问题

(i)算子T:C+[0,1]→C[0,1]有定义且连续,

(ii)对于任何ω∈C+[0,1],(Tω)(0)=β(Tω)'(0),(Tω)(1)=α(Tω)(η).

简单核验后我们得到:

引理2(1) ω*是问题(P)的解当且仅当ω*+ω0是(P')的解,

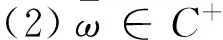
注:在具体问题中q(t)是可简便计算出的.

显然0<σ<1.

因此, 0

本文将使用下列控制函数,对于l>0,我们记

显然φ(l)≥Φ(l)≥0,Ψ(l)≥ψ(l)≥0,事实上,控制函数Φ(l),Ψ(l),φ(l)及ψ(l)都是可计算的,而且φ(l)和ψ(l)的计算是比较简单的.

引理3T:C+[0,1]→K是全连续的.

证 对于任何ω∈C+[0,1],有g(t,ω(t)-ω0(t))≥0,0≤t≤1 , 参照[8]中引理2.1和2.2的证明将可获证.

(1)‖Tω‖≤‖ω‖,ω∈∂Ω1,并且‖Tω‖≥‖ω‖,ω∈∂Ω2.

(2)‖Tω‖≥‖ω‖,ω∈∂Ω1,并且‖Tω‖≤‖ω‖,ω∈∂Ω2.

2 解的存在性定理

定理1假设存在两个正数a

(1)Φ(a)≤aA,Ψ(b)≥bB,特别地, φ(a)≤aA,ψ(b)≥bB,

(2)Ψ(a)≥aB,Φ(b)≤bA,特别地, ψ(a)≥aB,φ(b)≤bA,

则问题(P)至少有一个解ω*,满足ω*+ω0∈K,并且a≤‖ω*+ω0‖≤b.

证:仅证情况(1),由于a

则‖ω‖=a,0≤ω(t)≤a,0≤t≤1,于是

0≤g(t,ω(t)-ω0(t))≤Φ(a)≤aA,0≤t≤1.

根据引理3和2(3),我们有:

‖Tω‖

g(t,ω(t)-ω0(t))≥Ψ(b)≥bB,μ≤t≤ν

利用引理2(3),我们得到:

‖Tω‖

根据引理2,3和4知:问题(P)至少有一个解ω*满足ω*+ω0∈K,并且a≤‖ω*+ω0‖≤b.

同理可证情况(2)亦成立.

因为ω0(t)=Mp(t),我们有ω0(0)=Mβ(1-αη2)=j(0),ω'(0)=M(1-αη2),ω=kM,

注意到ω0(t)为凹函数,可知ω0(t)≤j(t),0≤t≤1.

于是aθq(t)>ω0(t),0

ω*(t)=(ω*(t)+ω0(t))-ω0(t)≥θq(t)‖ω*(t)+ω0(t)‖-ω0(t)> aθq(t)-ω0(t)>0.

由此,我们断言ω*是一个正解.定理获证.

利用定理1,我们可以建立下列多解性结论:

定理2假设存在3个正数a

(1)Φ(a)≤aA,Ψ(b)>bB,Φ(c)≤cA,特别地, φ(a)≤aA,ψ(b)>bB,φ(c)≤cA,

(2)Ψ(a)≥aB,Φ(b)

证: 我们仅证情况(1),因为Ψ:[0,+∞)→[0,+∞)连续,且Ψ(b)>bB知:存在两个正数b1,b2,使a

定理3假设存在n+1个正数a1

注1: 当β=0,即为文[8]中讨论的情况,本文结论是对文[8]结论的推广和改进.

注2: 定理的证明的关键是构造一个适用的锥,值得注意的是文[8]证明解和正解的存在性对本文的证明似乎是困难的.

注3: 本文不再要求θ为具体常数,而是将其放宽为0<θ<1的任何常数,推广了文[8]中结果.

由定理1情况(1)知:该问题至少有一个解ω*使ω*+p∈K且1≤‖ω*+p‖≤300.

[1] Liu Yansheng,Qi Aiqin.Positive Solutions of Nonlinear Singular Boundary Value Problem in Ab-stract Space[J].Computers and Mathematics with Applications,2004,47:683-688

[2] Ma Ruyun.The Nonlocal Problems for Nonlinear Ordinary Differential Equation[M].Beijing:Science and Technologey Press,2004(in Chinese).

[3] Ravi P Agarwal,Donal O'Regan.Some New Results for Singular Problems with Sign Changing Nonlinearities[J].Journal of Computational and Applied Mathematics ,2000,113:1-15.

[4] Gupta C P. Solvability of a Three-point Nonlinear Boundary Value Problem for a Second Order Ordinary Differential Equation[J].J.Math.Anal.Appl.,1992,168:540-551.

[5] 赵增勤.非线性奇异微分方程边值问题的正解[J].数学学报,2000,43(1):179-188.

[6] 杨志林,孙经先.非线性二阶常微分方程组边值问题的正解[J].数学学报,2004,47(1):111-118.

[7] Guo Yanping,Ge Weigao,Dong Shijie.Two Positive Solutions for Second Order ThreePoint Boundary Value Problems with Sign Changing Nonlinearties[J]. Acta Mathematicae Applicatae Sinica，2004,27(3):522-529(in Chinese).

[8] 姚庆六.半正二阶三点边值问题的解和正解[J].应用数学学报,2007(30):209-217.

[责任编辑：王军]

Solutions and multiple solutions of second-order three-point boundary value problems

CUI Yan,LI Qun

(College of mathematics and statistics, Fuyang Normal College, Fuyang 236000,China)

By using a fixed point theorem in cones , the existence of solutions and multiple solutions is considered for a nonlinear second-order three-point boundary value problem .

semipositone nonlinearity; existence ;multiplicity

2015-05-15

安徽省自然科学基金项目(2014KJ013);阜阳师范学院校级自然科学基金项目(2014FSKJ03ZD);安徽省自然科学基金项目(2014KJ001)

崔艳(1980-),女,山东德州人,阜阳师范学院讲师,应用数学专业硕士生,主要从事非线性泛函分析研究.

O175.8

A

1672-3600(2015)09-0011-05