一个含有2n个非零元的极小谱任意符号模式矩阵

赵丽娟，邵燕灵

(中北大学 理学院，山西 太原 030051)

一个含有2n个非零元的极小谱任意符号模式矩阵

赵丽娟，邵燕灵

(中北大学 理学院，山西 太原 030051)

研究了一个含有2n个非零元的符号模式矩阵，并运用幂零—雅可比方法和幂零—中心化方法证明该符号模式是极小谱任意的.

符号模式；谱任意；幂零—雅可比；幂零—中心化

0 引 言

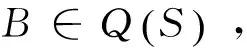
引理 2[4](幂零-中心化方法)设S是n×n符号模式，B是S的一个指数为n的幂零实现.如果B的中心中满足条件C°BT=0的矩阵C只能是零矩阵，那么，S及其每一个母模式都是谱任意的.

1 主要结果

定理1当n≥7时，S的所有母模式都是谱任意的.

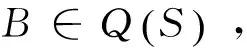
其中ai<0,i=1,...,n-4,n，aj>0,j=n-3,n-2,n-1.下面分别用两种不同的方法证明S的所有母模式都是谱任意的.

将上式第i行的λ倍加到第i+1行，i=1,2,...,n-1，然后再按第2,3,5,...,n-4,n-2,n-1,

n列依次展开，得：

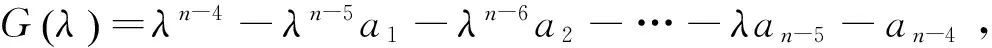
(1)

所以

(2)

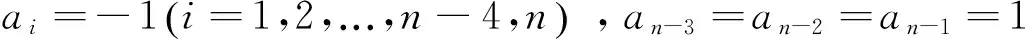
且

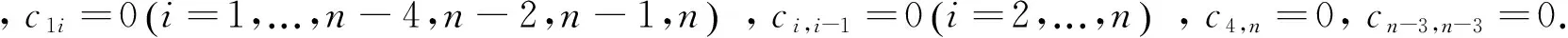
定理2S是极小谱任意的.

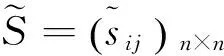
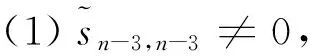
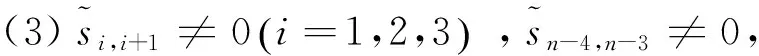
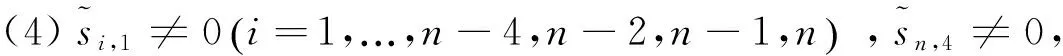
综上所述，S是极小谱任意符号模式.

[1] Leslie H. Handbook of Linear Algebra[M]. Bocaraton: CRC Press, 2007.

[2] Drew J H, Johnson C R, Olesky D D, et al. Spectrally arbitrary patterns[J]. Linear Algebra and its Applications, 2000, 308(1): 121-137.

[3] Britz T, McDonald J J, Olesky D D, et al. Minimal spectrally arbitrary sign patterns[J]. SIAM Journal on Matrix Analysis and Applications, 2004, 26(1): 257-271.

[4] Garnett C, Shader B L. The Nilpotent-Centralizer Method for spectrally arbitrary patterns[J]. Linear Algebra and its Applications, 2013, 438(10): 3836-3850.

[5] Cavers M S, Vander Meulen K N. Spectrally and inertially arbitrary sign patterns[J]. Linear Algebra and its Applications, 2005, 394:53-72.

[6] Gao Yu-bin, Shao Yan-ling. A spectrally arbitrary patterns[J]. Advances in Mathematics, 2006,35(5):551-555.

[7] Gao Yu-bin, Shao Yan-ling, Li Zhong-shan. A Note on spectrally arbitrary sign patterns[J].JP Journal of Algebra , Number Theory and Applications, 2008, 11: 15-35.

[8] Bergsma H, Kevin N, Vanderm, et al. Potentially nilpotent patterns and the Nilpotent-Jacobian method[J]. Linear Algebra and its Applications, 2012, 436: 4433-4445.

[9] Garnett C, Shader B L. A proof of the Tn conjecture: Centralizers, Jacobians and spectrally arbitrary sign patterns[J]. Linear Algebra and its Applications, 2012, 436(12):4451-4458.

[责任编辑：王军]

A class of minimally spectrally arbitrary pattern matrix with 2n nonzero entries

ZHAO Lijuan, SHAO Yanling

(School of Science, North University of China, Taiyuan 030051, China)

In this paper we give a new minimally spectrally arbitrary patterns with2n nonzero entries.The sign pattern has been proved to be minimally spectrally arbitrary by using Nilpotent-Jacobian method and Nilpotent-Centralizer method.

sign pattern;spectrally arbitrary; nilpotent-Jacobian; nilpotent-centralizer

2014-12-09

山西省回国留学人员科研资助项目(12-070)

赵丽娟(1989-),女,山西大同人,中北大学硕士研究生,主要从事组合数学方面的研究.

O157

A

1672-3600(2015)09-0007-04