多声道超声流量计数值积分方法优化
2015-01-13张皎丹郑丹丹
张皎丹 郑丹丹 张 涛 赵 丹 李 波
(天津大学电气与自动化工程学院天津市过程检测与控制重点实验室,天津 300072)
随着能源和水资源的全球性匮乏,一批关系国计民生的大型水利工程和引水调水工程在我国迅速发展,如三峡水利枢纽及南水北调工程等。这些工程项目中经常包含一些口径和流量都很巨大的管道,如水电站机组进水管道等,常规流量计无法适应。近年开发的多声道超声流量计较好地解决了大口径水流量测量的技术难题,流量计制造不受管道口径的限制,多声道配置可以适应较为复杂的流道结构和流态分布,故超声流量计已成为大口径水流量测量的最佳技术选择[1]。
超声流量计在计算管道流量时所采用的数学模型的准确度对整个测量精度有着非常重要的意义。目前普遍使用的平行布置多声道超声流量计用Gauss-Jacobi积分方法来计算管道体积流量,其各声道高度和权重系数的确定都是针对理想的充分发展管道流动,而在非理想管道条件下,如果继续采用相同的数值积分方法会造成非理想管道流动引入的附加不确定度。
针对这一问题,国内外学者也进行了深入的研究。但是前人对此课题的研究均是在理想流场中对理想流动进行积分方法的改进,笔者基于非理想管路的流态分布来对数值积分方法进行优化研究,并选取了工业现场常见的单弯头流场作为研究对象,通过单弯头理论模型和实流实验分别进行验证,从而提高了超声流量计的测量精度。
1 数值积分方法优化①
1.1 Gauss-Jacobi积分方法
超声流量计利用超声波在流体中传播的时间存在差异的特性[2],由置于待测截面两侧的一对换能器测量超声波顺流与逆流传播的时间td,i、tu,i,得到相应声道上的平均轴向速度(简称声道速度),其原理如图1所示。

图1 圆形管道声道速度的测量原理
平均轴向速度vi的计算式为:
(1)
式中i——声道数号,i=1,…,N;
Li——声道长度;
N——声道数,此处取N=4;
φi——声道角。
为了提高流量计的测量准确度,在待测截面上平行地布置多条声道,获得的声道速度可以代表待测截面上相应平行条带内的平均速度,如图2所示,图中zi为声道高度,li=Lisinφi为声道宽度,并依据各声道所占的权重系数ωi,用加权求和的方法计算流量。
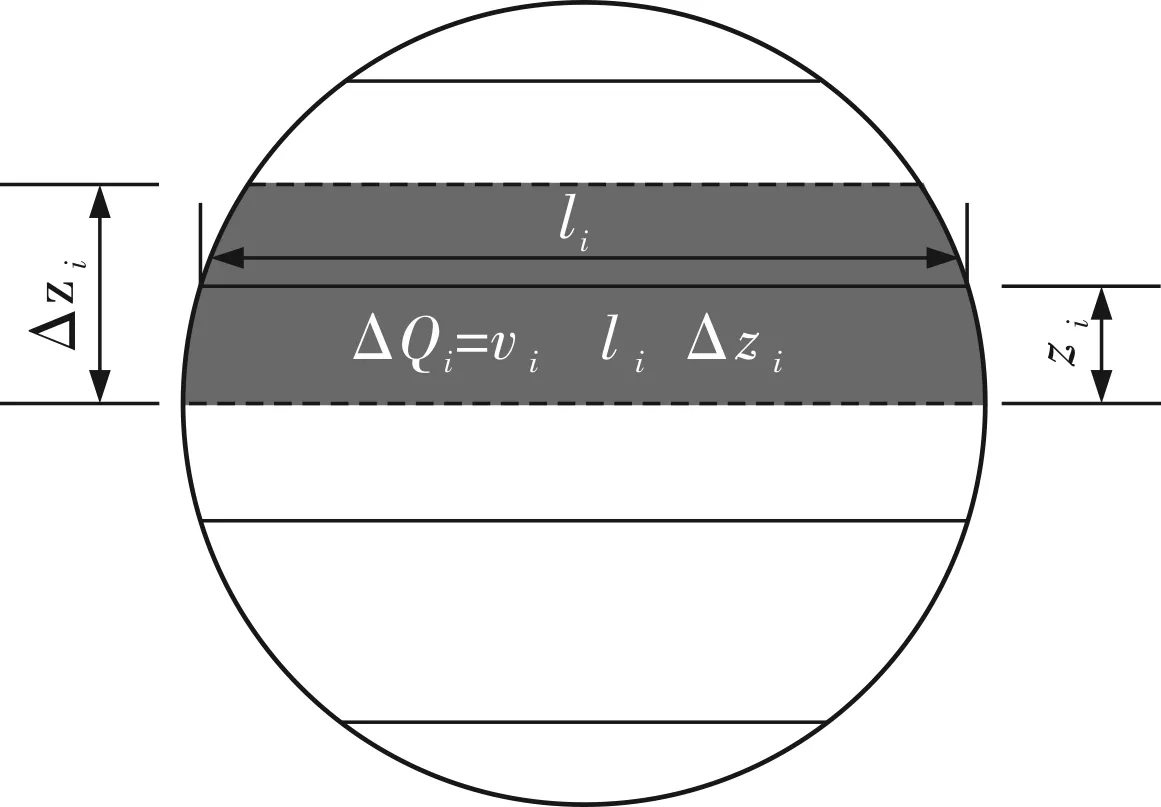
图2 圆形管道数值积分示意图
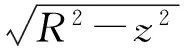
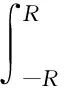
(2)


将式(2)变形可得:
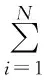
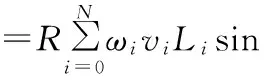
(3)
相对于梯形公式及辛普森公式等插值积分要求采样点固定甚至等距,Gauss积分方法则是建立在采样点个数一定且位置自由选择的基础上,是目前积分精度最高的一种方法。圆管中的超声流量计一般采用Gauss-Jacobi积分法来确定声道的最优位置ti和相应的权重系数ωi[3]。
按照以下公式即可求得权重系数的值[4]:
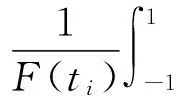
(4)
(5)
IEC41和PTC18规程中已有计算好的不同声道数N的声道高度和权重系数,一般依此位置和系数安装超声换能器并计算流量。
实际上,在Gauss-Jacobi积分方法的使用中,认为圆管中速度为理想均匀分布,即v(tR)=1。而对非理想流场而言,由于超声探头和上游阻流件(弯头及蝶阀等)的存在,会对管道表体处流态分布产生较大的影响,此时若继续使用Gauss-Jacobi积分方法来计算管道流量,势必会造成非理想管道流动引入的附加误差,影响超声流量计的测量性能。
1.2数值积分方法改进
针对非理想流场条件下Gauss-Jacobi积分方法的优化问题,改进切入点是用实际的速度分布表达式来代替理想的速度表达式v(tR)。当超声流量计表体段装有探头和上游存在阻流件时,表体段流场较为复杂,找到一个能很好地表征实际管路流态分布的速度表达式很困难,为获得流态分布信息,基于计算流体动力学(CFD)仿真结果离散化声道所在截面,将离散的速度值集合作为实际管路的流速分布。具体改进方案和验证方法如下:
a. 在超声流量计表体段的声道截面上建立199条声道,提取并计算出各声道的速度值v(tiR)。

c. 计算权重系数值。将式(4)、(5)离散化。
步骤c的计算公式为:
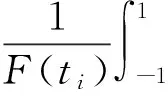
(6)
(7)
其中j=1,…,M,M为199。
利用式(6)、(7)可求取新的权重系数。
针对Gauss-Jacobi积分方法的优化过程,有两点需要说明:
a. 在Gauss-Jacobi积分方法改进过程中,只对权重值进行了优化,并没有改变其声道高度。这是由于实流实验所用样机的结构形式已定,声道高度无法改变,故要想将优化后的积分方法用于实流效果的验证,只进行了权重系数的优化。
b. 由式(6)可以看出,若所建声道数M太小,则离散化后的各项求和结果不能准确地逼近原积分结果,影响新权重系数的计算准确度。对比199条声道和399条声道的优化结果见表1,可以看出在两种声道布置下,其相对误差仅差0.06%,而超声流量计一般测量精度为1.00%,此差别可忽略不计,故认为提取声道截面上199条声道的速度值已经可以准确地反映表体处流场的实际流态分布情况,但若想提高测量精度,可以适当地增加声道数。笔者选取M=199。

表1 不同声道数下实流实验结果对比
2 优化积分方法的验证
以下将从速度分布的理论模型和实流实验两方面分别验证优化积分方法的有效性。笔者选取了工业现场常见的单弯头流场作为研究对象。为便于处理数据,定义了相对误差:
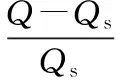
(8)
式中Q——超声流量计的测量值,即基于式(4)的计算结果;
Qs——超声流量计的标准流量值。
2.1单弯头理论模型验证
Salami提出的Salami公式可准确地描述出不同非理想管道条件下流场的速度剖面理论模型,笔者对单弯头下游的速度剖面模型进行优化验证,此模型的Salami公式为[5]:
(9)
其中θ表示的角度范围为0~2π,圆的半径设定为1。图3为单弯头下游剖面的速度等值线,图中α为旋转角。
通过此模型的Salami公式,分别提取不同旋转角下的199条声道的线平均速度,按上述优化方法验证步骤对Gauss-Jacobi积分方法进行改进,得到新的权重系数(表2),不同旋转角下的改进情况见表3。

图3 单弯头下游速度等值线

表2 不同旋转角下4个声道修正后的权重系数
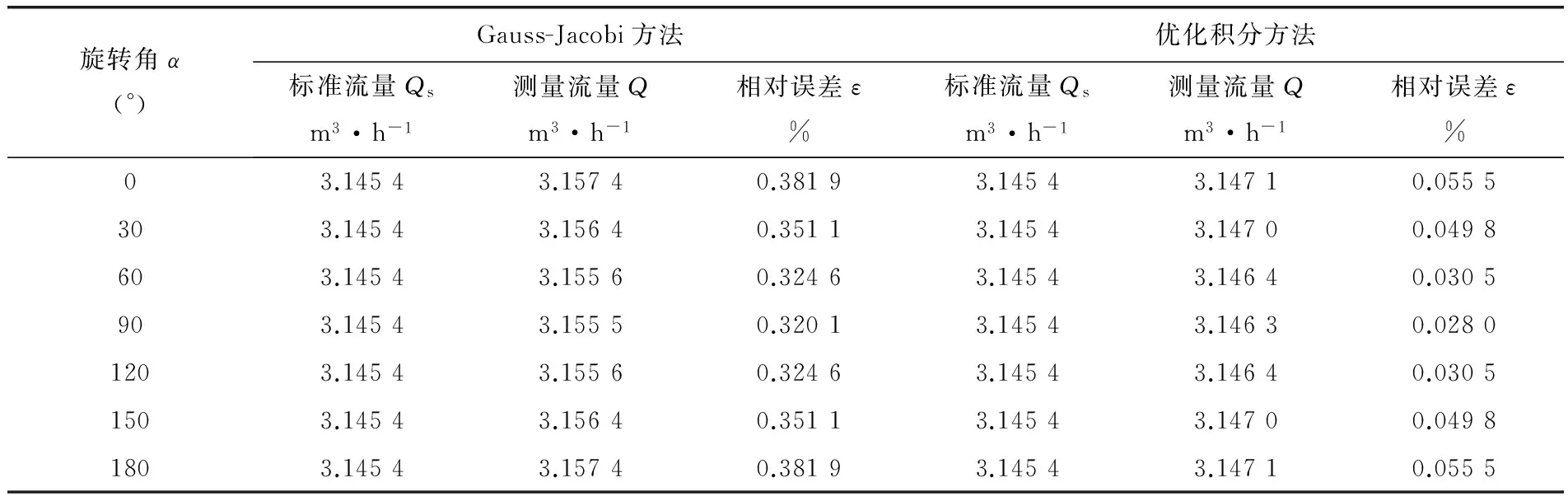
表3 不同旋转角度修正结果
由表3可以清晰地看出,在不同旋转角下,优化后,相对误差得到明显改善,Gauss-Jacobi方法的相对误差在0.32%~0.39%之间;而优化的数值积分方法的相对误差最大为旋转角为0°时,误差只有0.055 5%。
2.2单弯头实流实验
鉴于理想Salami模型,与实际安装管路单弯头下游流场有差别,为验证实际流场中优化的数值积分方法的有效性,开展了单弯头实流实验。
本实流实验使用的是独立加工设计的四声道超声流量计,其声道位置按照Gauss-Jacobi方法中的声道位置进行布置。实验依托于天津市过程参数检测与控制重点实验室的水流量标准装置,采用标准表法对超声流量计进行测量,实验管径D为100mm,水流量标准装置精度可达0.05%。超声流量计前后直管段长度均为10D,为了尽量消除单弯头上游阻流件(弯头及蝶阀等)对流场的影响,在单弯头上游设置了约30D的直管段。
为获得优化后的权系数,对实际管路进行仿真。为保证仿真尽可能地符合实流实验,建立仿真模型与实流实验管路完全一致,如图4所示。按上述优化方法验证步骤对积分方法进行改进,从而获得入口速度为0.296、0.390、1.618、3.386、5.132m/s共5个流速点下的权重系数(表4)。
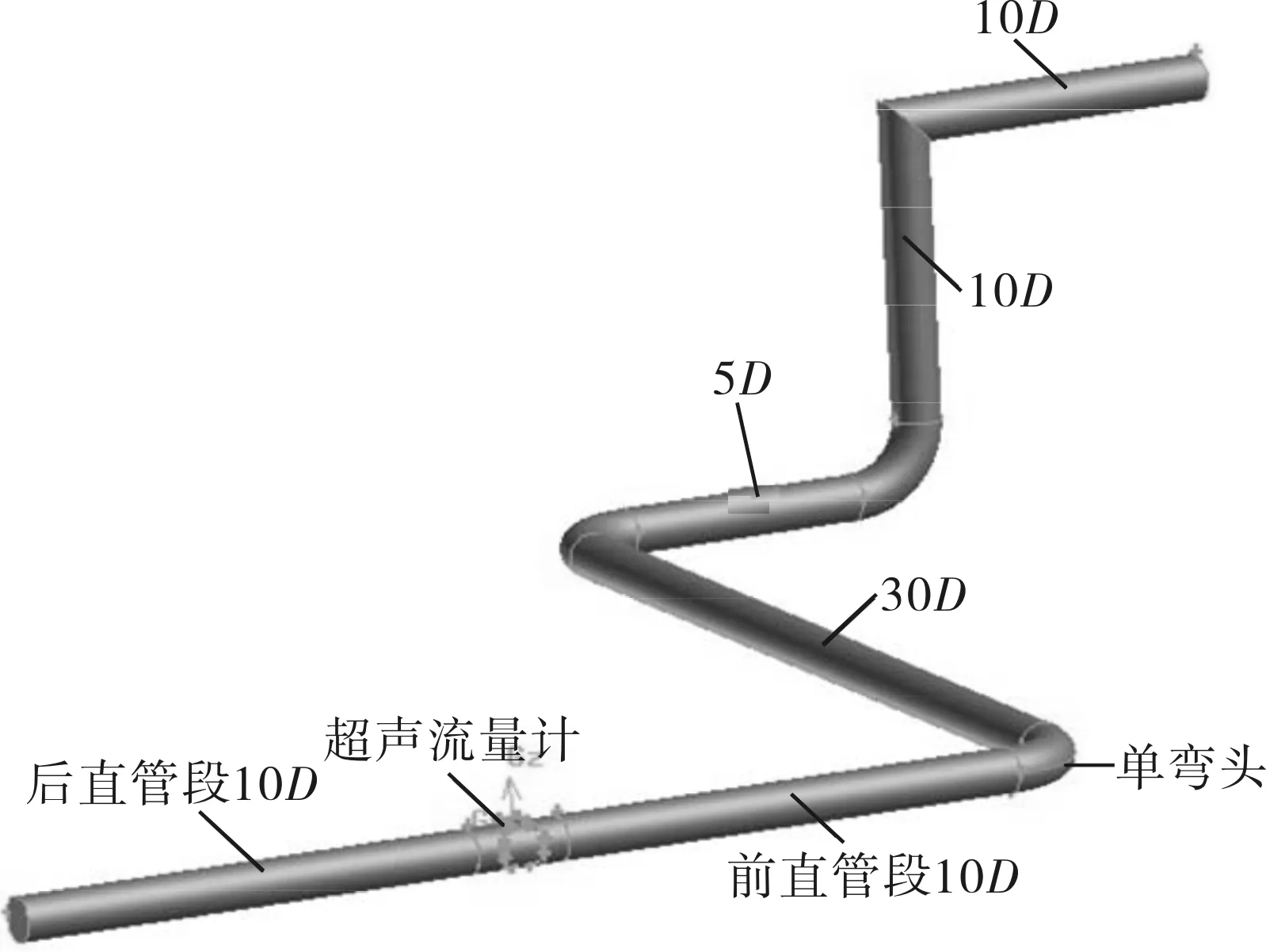
图4 单弯头条件下的仿真模型
将得到的平均权重系数代入到实流实验数据中,验证其对实流实验的改进效果(表5)。可以清晰地看出单弯头条件下优化前后的对比。在实流实验中,中高流速点处都有明显改善,优化后误差降低了3.60%左右。分析小流量点处优化无明显改善的原因,认为积分方法改进是基于仿真数据优化权重系数,和实流实验之间存在一定的误差,在小流量点处,仿真和实流实验的误差较大,影响了实流实验最终优化的结果。
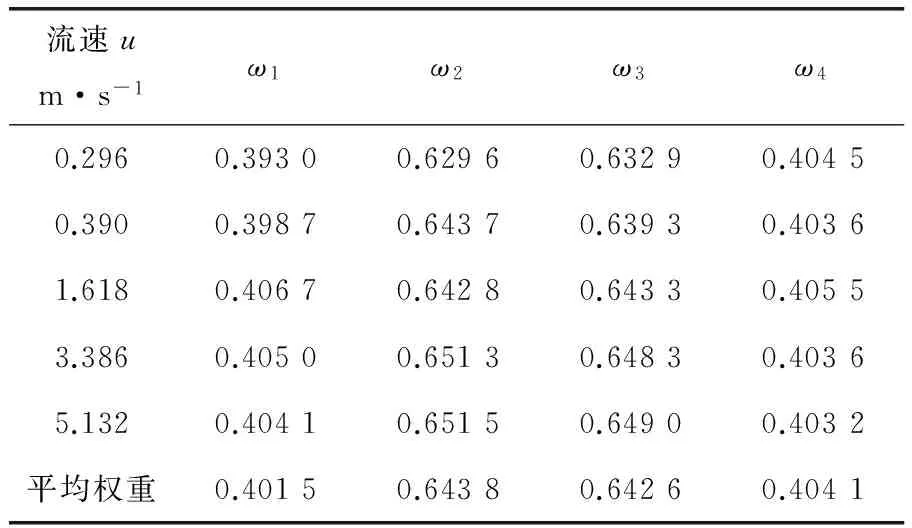
表4 4个声道修正后的权重系数
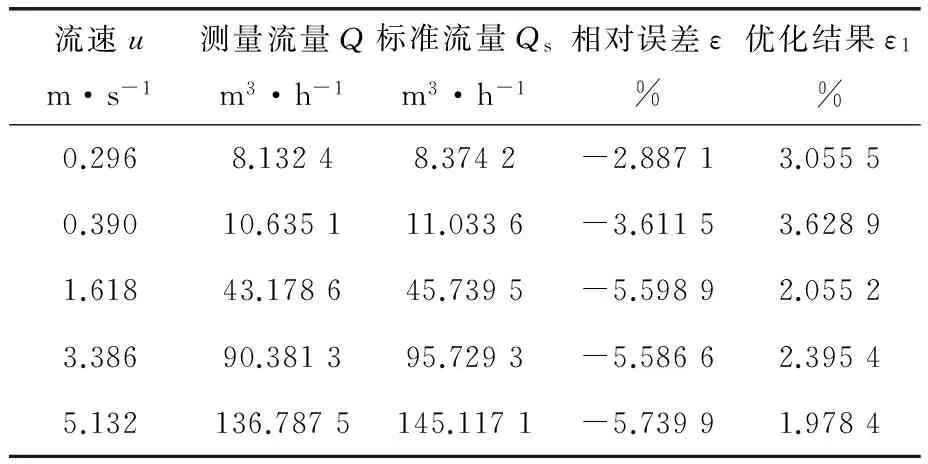
表5 实流实验中不同流速修正结果
3 结论
3.1提出Gauss-Jacobi积分方案的优化方法。基于CFD仿真方法,在表体段建立平行布置的199条声道,提取各声道的线平均速度,用这些离散的速度值组成的集合来代替实际管路的流态分布;计算各流速下的截面流动方程F(t),进而求取新权重系数。
3.2单弯头理论模型的改进效果要明显优于实流实验改进的效果,对单弯头理论模型而言,优化后超声流量计测量误差绝对值均在0.06%以内,精度提高了0.30%。对实流实验来说,小流速点处修正前、后误差相近,中高流速点的误差降低了3.60%左右。
[1] 霍殿中.大流量测量和多声路超声流量计[C].全国流量测量学术交流会论文集.郑州:中国计量测试学会流量计量专业委员会,2006:158~166.
[2] 王新民,杨天行,李淑芬.应用数值方法[M].长春:吉林教育出版社,1992.
[3] JJG1030-2007,中华人民共和国国家计量检定规程超声流量计[S].北京:中国标准出版社,2007.
[4] Tresch T, Gruber P. Presentation of Optimized Integration Methods and Weighting Corrections for the Acoustic Discharge Measurement[C].International Conference on Hydraulic Efficiency Measurement. Piscataway,NJ,USA:IEEE,2008:1~14.
[5] Moore P I, Brown G J,Stimpson B P.Ultrasonic Transit-time Flowmeters Modelled with Theoretical Velocity Profiles: Methodology[J]. Measurement Science and Technology,2000,11(12):1802.
