套管试压过程中连续波波动的幅频特性研究

刘 均 汪 鑫 陈 晨

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

在目前的钻井生产过程中，已使用套管水泥面控制器检定方法测量套管的打开压力和稳定性，其工作过程是将销子安装在套管中，然后对套管内的水流加压，当压力增加到某一定值时，在销子断裂的瞬间读出系统压力，由此得到测试结果，即根据剪销打开压力来检定套管的打开压力和稳压性[1～3]。观察这种方法得到的数据，能够发现水泵在工作过程中，因其运作原理会使得剪销打开压力的最大值、最小值和平均值之间的差值特别大[4,5]。

以解决上述问题并提高工作效率为目的，对现有设备进行改造，分析这种现象发生的原因。在管道上安装压力传感器进行压力值的测量，在工作台上增加了测量显示装置来实时显示测量数据。在整个系统运行过程中，通过压力传感器的数据显示，发现管道中的压力变化剧烈，这对信息的测量和数据的采集十分不利。因此对管道内压力波的波动加以抑制是必要的。

当前对于压力波的研究大多集中于单个波形的波动情况，但是生产实际中，是以管道中的连续波动为研究角度的。在此，对经典的管道内压力传递矩阵模型进行分析，推导相应的数学模型，来描述管道内的压力波波动并设计滤波器来抑制压力波的波动，最后设计了相关的测量系统。

1 压力波波动传递模型分析

对整个套管内流体压力波波动的情况进行观察与分析后，对管道内压力波波动的形式有了初步了解，根据文献[6]可以得到管道中出现连续波动情况下压力幅值的变化情况，以及管道内压力与流量幅值的传递矩阵模型(图1)。

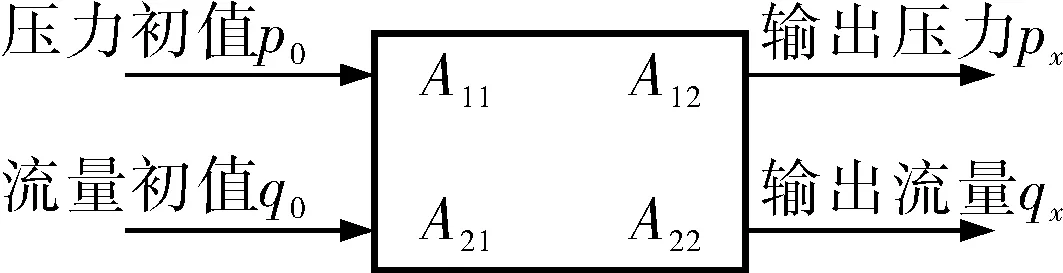
图1 管道内压力与流量幅值的传递矩阵模型

通过对模型的分析与整理，得到单个直管道的传递矩阵为：

(1)

A11=cosh(bx),A12=-Zcsinh(bx)

A21=-sinh(bx)/Zc，A22=cosh(bx)

从式(1)可以看出压力波波动并非随着频率的变化而线性衰减。

为了进一步分析压力波波动的衰减情况，对照流体运动与电路的相应理论，可以得到套管内任意位置的阻抗表达式：

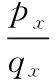
(2)

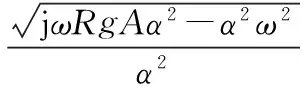
式中A——管道横截面积；

a1、a2——可通过边界条件获得的定值常数；

g——重力加速度；

x——管路轴向坐标；

α——波的传输速度。

根据实际情况对方程组进行改写，可以得到如果将输出端的压力与流量之比po/qo定义为终端阻抗Zr，可以认为它是负载，体现管道出口对管道中流体流动的影响，然后推导出输出端po与输入端pi的比值关系：

(3)

根据上述推导的压力振幅比与频率的关系，进行模型建立与模型仿真，结果如图2所示，图中波形显示出了输出端po与输入端pi的比值在不同波动频率下的变化情况，可见压力振幅比与频率呈现了波动性的变化，从整体的角度观察能够发现，伴随着频率的增加压力振幅比是波动性衰减的，并且在衰减过程中还存在着激增现象，正是由于激增现象引起了在套管中临界压力值测量时误差的产生。

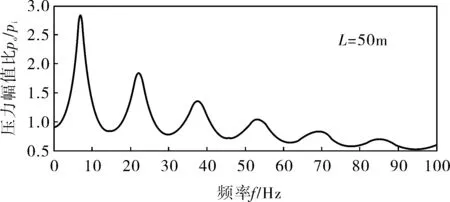
图2 管道内压力幅值比与频率的关系曲线

2 外接容器对管道波动传递的影响

上述模型也适用于多管串联管道，对于管道直径不同的L1和L2连接管道(图3)，可以分别计算出L1和L2的传递矩阵ML1和ML2，以及连接点D处的矩阵MD。根据图3的串联管道结构，从机械振动的角度进行分析，从而获得串联管道的传递矩阵为：

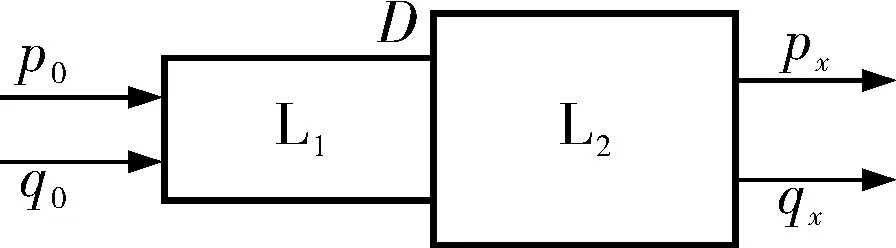
图3 多管串联管道结构示意图

同理可以获得，当管道有分支管时，只需写出分支点的传递矩阵就可以将分支管的影响引入表达式。为了达到滤除管道中压力波波动的目的，设计如图4所示的滤波器。

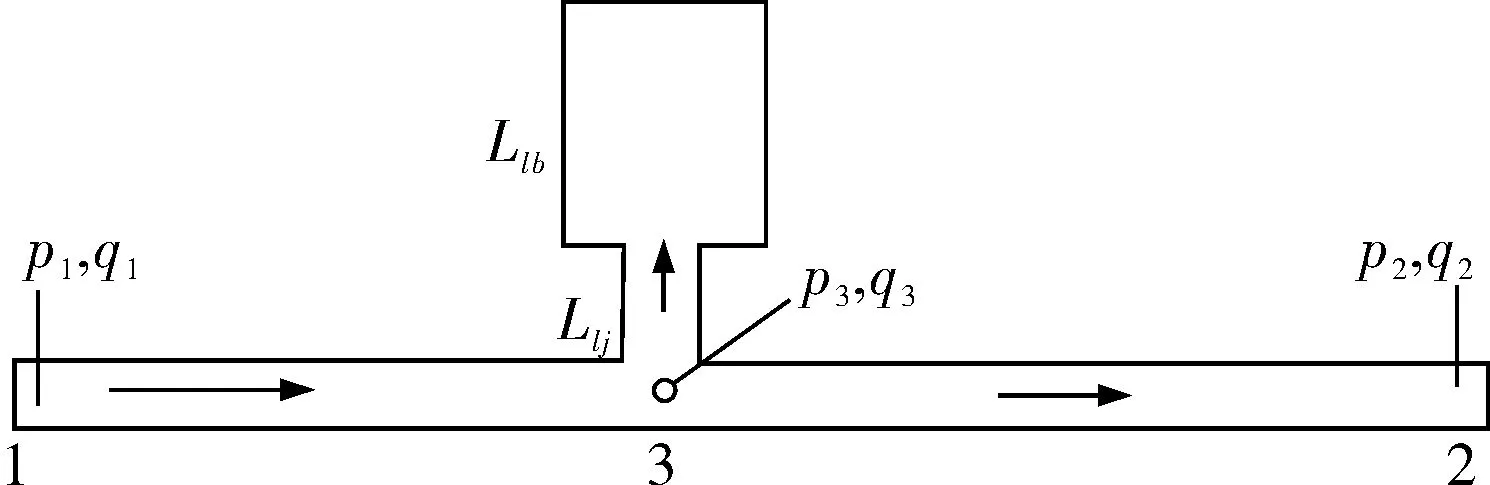
图4 滤波器结构示意图

此滤波器由两端相连的管道构成，细管道是压力传递管，粗管道是滤波器，在管道的1端输入流体，其压力幅值为p1、流量幅值为q1；在管道的2端输出流体，其压力幅值为p2，流量幅值为q2；在管道的连接点3处各分支的压力值相等且遵循流量总量守恒定律，即p1=p2=p3和q1=q2+q3，连接点3处的传递矩阵为：

(4)

在整个滤波系统中1、3端间的传递矩阵为M13，3、2端间的传递矩阵为M32，则整个管道L的传递矩阵ML为：

ML=M13·M3·M32

(5)

于是套管内压力波波动的传递可表示为：

(6)

由于外接滤波器的连接管较短，滤波器与连接管内的流体基本不流动，忽略滤波器与连接管中的摩擦力，可得连接点处的阻抗为：

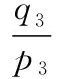
(7)

根据三角函数的关系tan(x)≈x，可以得到连接点处的阻抗为：

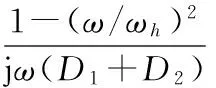
(8)

D1=AlbLlb/(ρα2)

D2=AljLlj/(ρα2)

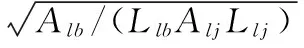
式中Alb、Llb——管道上外接滤波器的管道截面积与长度；

Alj、Llj——外接滤波器圆柱容器的截面积与长度。

当管道此处的阻抗ZR为零时(即ωh=ω)，表明压力波波动通过此处后衰减为零，因此可以通过合适的谐振频率ωh设计滤波器尺寸，使其与水泵压力频率相等，这样就可以达到滤除水泵压力波波动的目的。

对此带滤波器的模型进行仿真，得到此时管道的幅值频率特性曲线，输出端po与输入端pi的比值在不同流体波动频率下的变化规律，如图5所示。可见，压力振幅比与频率呈现了波动性的变化，对带滤波器管道的幅值频率特性曲线进行观察，能够发现伴随着频率的增加，输出端po与输入端pi的压力振幅比是波动性衰减的。

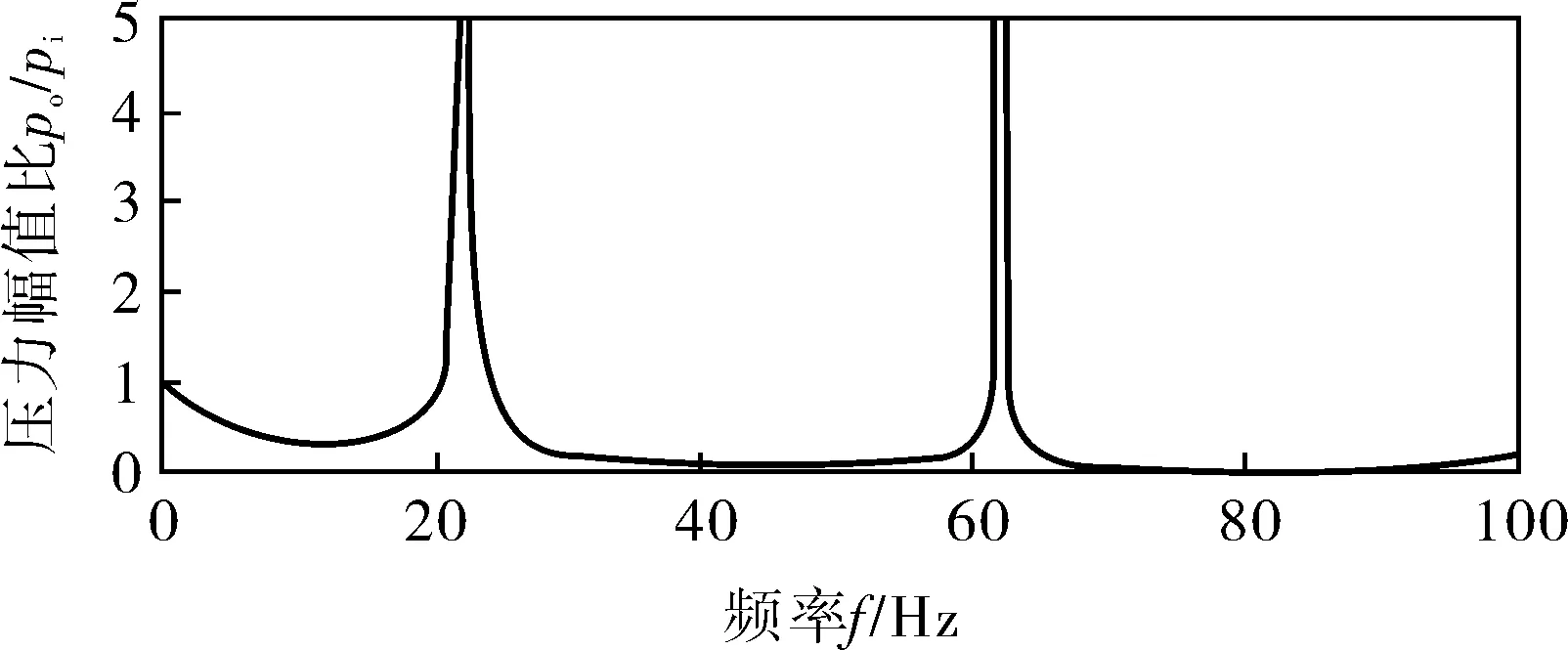
图5 带滤波器管道的幅值频率特性曲线

由仿真结果可以看出，加入了滤波器后，管道的频率幅值特性与图1相比发生了改变，振荡在某频率间得到了抑制，但是在某些频段振荡加强。因此，谐振频率的选取至关重要，在确定了谐振频率后，其附近的信号也有很大衰减，可以利用这种滤波器的特性完成对泵压波动的滤除。

3 应用

笔者设计了一个能够准确对剪销打开压力进行测量并实时给出测试信息的测量系统，如图6所示。通过对水泵结构的了解，设计并制作出相应的滤波器；在管道上安装压力传感器，此传感器采用半导体应变方式，全不锈钢封焊结构，具有良好的防潮和介质兼容性。传感器的主要参数决定了系统的测量精度和速度，主要完成管道内压力波波动的压力测量。整个系统由C8051F020单片机控制，LED实时显示测量结果，并通过RS232总线传输到上位机界面显示数据，同时进行后期的数据处理。

图6 套管剪销打开压力测量系统示意图

3.1 测量系统电路

在测量系统中，压力传感器需要24V(DC)供电电压，量程0～30MPa；介质温度-20～85℃；密封等级IP65；采样速度10～50次/s。机械振动频率在20～1 000Hz时，输出变化小于0.1%FS的振动影响，内有大于2 000MΩ的绝缘电阻；电流输出范围4～20mA。在管道中，压力传感器采集压力波波动数据，以电流形式输入到系统中，后接电阻，以电压的形式通过INA122放大器对数据进行处理。单片机处理压力传感器采集数据的部分电路如图7所示。

测量系统中，由于C8051F020单片机内嵌RS232总线控制器，因此在外部电路中添加RS232总线收发器(SP3223总线收发器)完成数据的发送与接收，将压力传感器采集的数据传送到上位机并以软件方式显示。

测量系统通过单片机的IO口驱动HD7279A芯片，此芯片具有串行接口，是一个可驱动8位共阴式数码管的智能显示驱动芯片，在电路中完成LED显示功能。将压力传感器所采集的压力波波动数据实时显示在8位数码管上。8位数码管分为1、2两屏，可以在数码管上观察管道内压力波的波动情况，并可通过1屏显示数据，直观地获得剪销打开压力。

3.2 系统软件实现的关键技术

在整个测量系统中，首先通过压力传感器对套管内的压力波波动进行测量，由测量控制装置对采集到的4～20mA电流信号进行转换，不仅可以通过总线传递到上位机，而且可以LED双屏显示，在显示测量最大值的同时还能实时观测到套管内的压力波波动。在压力波波动测量过程中，有压力开始测量的压力上升状态(加压过程S1)、压力测量值超过临界阈值的可记录状态S2和测量结束状态S3。软件工作状态如图8所示。

图7 单片机处理压力传感器采集数据的部分电路

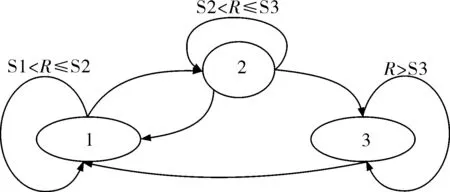
图8 软件工作状态示意图

在整个系统初始化过程中，设置了3个阈值T1、T2、T3，将最大值Rm与测量值R进行比较，当R大于S1并且不大于S2时，系统进入T1状态；系统在T1状态下运行，当R大于S2并且不大于S3时，系统进入T2状态；系统在T2状态下运行，当R大于S3时系统进入T3状态；系统在T3状态下运行，当R大于Rm时，Rm被重新赋值。当测试结果达到最大值后会瞬间减小，测试步骤循环往复直至测试结束。在T1、T2与T3的共同作用下，双屏显示器不仅显示测量过程中压力的实时数据，还在不断比较之后，显示最大压力值。实现了过程清晰、结果准确的目的。

整个测量系统主要是观察管道内的压力波波动情况，通过对水泵信息的分析，设计相应的波动滤波器，在笔者设计的测量和显示装置上，可以很直观地观察压力波的波动情况。在添加滤波器后，相关频率波动得以抑制，同时在滤波器结构准确的情况下，该装置能够精准地为工作人员提供套管的打开压力和稳定情况。测量系统测量出的管道内压力变化曲线如图9所示，可以看出10s内管道内压力的变化情况，也获得了套管的打开压力值。

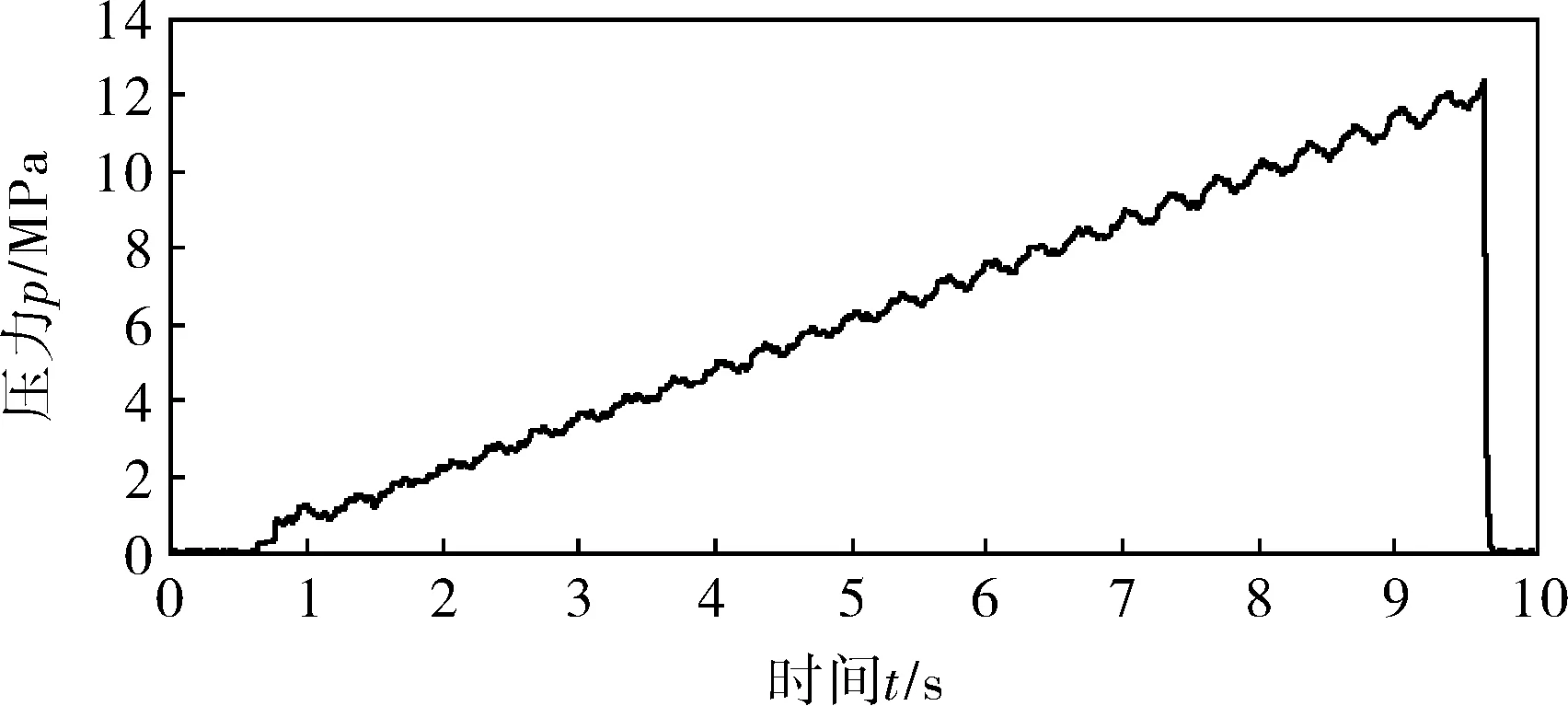
图9 管道内的压力测量数据曲线

4 结束语

通过对套管水泥面控制器检定方法的分析，以及对套管管内液体波动情况的观察，明确液体波动现象；以压力振幅传递矩阵为依据，对管道内压力波的波动进行建模与分析，发现管道结构对波动的影响；以抑制水泵引发的压力波波动为目的，得到了谐振频率，确定了压力波波动滤波器的结构，设计相应的测量系统；测试过程中将测量与显示相结合，实时显示管道内压力的波动情况。而且，此种滤波器只是过滤了某一固定频率的波动，它在一定程度上减小了误差的产生。

[1] 吴柳根,马建忠,宁学涛,等.膨胀悬挂器技术在石油工程中的应用[J].石油矿场机械,2012,41(9):59～63.

[2] 胡荣霞,李金海.泵系统中的水锤与阀控制的研究综述[J].水利科技与经济,2006,12(12):816～818.

[3] 曹慧哲,贺志宏,何钟怡.有压管道水击波动工程及优化控制的解析研究[J].工程力学,2008,25(6):22～26.

[4] Ghidaoui M S,Zhao M,McInnis D A.A Review of Water Hammer Theory and Practice[J].Applled Mechanics Reviews,2005,58(1):49～76.

[5] 王翔,王瑞和,纪国栋.井筒内钻井液连续脉冲信号传输频率相关摩阻模型[J].石油学报,2009,30(3):444～449.

[6] Liu J,Yuan F.Wireless MWD Continuous Wave Signal Transfer Model and Simulation[C].2013 Third International Conference on Instrumentation,Measurement,Computer,Communication and Control(IMCCC)Washington:IEEE,2013:247～251.