气-固流化床压力脉动信号的多尺度熵分析

徐金晖 巴晓玉

(沈阳黎明航空发动机(集团)有限责任公司运行保障中心，沈阳 110043)

气-固流化床的压力脉动信号包含了丰富的反映其运行状态及流型转变等的信息，是气泡特性、颗粒特性及流化床的几何条件等多种因素相互耦合的综合动态反映。通过压力脉动信号可以获取气泡的行为、颗粒的运动状态及流型的转变等工作状态，因此研究压力脉动信号的内在本质对深入了解气-固流化床动力学特性有重要意义。相比于其他参数，在恶劣环境下压力信号具有易测量、成本低、响应速度快、安全性能好及工作可靠性高等特点，因此利用压力脉动信号表征流化床内的动力学特性被广泛研究。

目前，基于混沌、分形、耗散结构、时域分析、频域分析及状态空间等方法对流化床内脉动行为的研究日趋增多[1～4]。赵明阳等通过高阶统计量对气-固流化床压力脉动信号进行研究，结果表明流化床压力脉动信号是非高斯性，并提出特征值T，获得了不同流态下信号偏离高斯性的程度[5]；秦伟刚等利用希尔伯特-黄变换(HHT)中的经验模态分解(EMD)方法和盲信号分离-三阶累积量方法对压差信号进行分析，结果表明EMD和三阶累积量结合能有效揭示气-固两相流的压差特性[6]；王春华等采用分形标度计算方法对气-固流化床压力脉动信号进行分析，研究了分形标度值与最大Lyapunov指数间的关系，得出分形标度值对于混沌特性具有表征作用的结论[7]；张少峰等对压力脉动信号进行了时域、频域和自相关性分析，表明流体流动和颗粒运动所引发的压力脉动能量频带分别集中在0～10Hz和30～40Hz，压力脉动的概率密度近似呈正态分布[8]；文献[9，10]对垂直上升气-液两相流电导脉动信号采用多尺度熵进行分析，根据不同尺度的多尺度熵脉动特征揭示了不同流型的动力学特性。

笔者将针对气-固两相流化床内的压力脉动信号进行多尺度熵分析，以进一步了解流化床内的流动特性，以指导气-固流化床的实际生产。

1 理论基础

1.1 样本熵

给定一个长度为N的时间序列x={x(1),…,x(i),…,x(N)}，其样本熵的计算步骤如下：

a. 构造一个m维的模板向量xm(i)={x(i),x(i+1),…,x(i+1-m)},1≤i≤(N-m+1)；

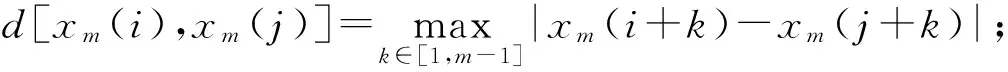
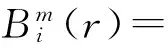
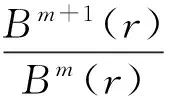
1.2 多尺度熵

多尺度熵算法的原理与步骤如下：

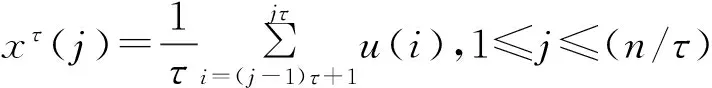
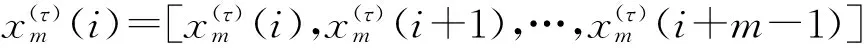
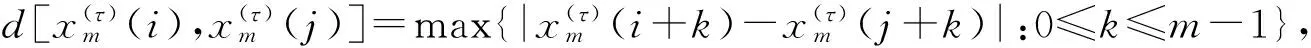
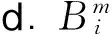
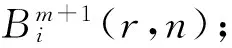
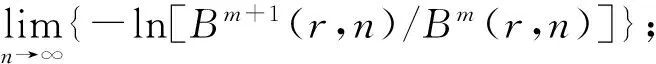
g. 计算粗粒化后各个尺度τ所对应的时间序列的样本熵值，即得到多尺度熵。

为便于分析，上述计算过程中序列的匹配长度m取2，阈值r为原始时间序列标准差σ的0.10～0.25倍，数据长度8 000点，最大粗粒化尺度20。

2 压力脉动信号的获取

实验装置由动力系统、循环流化床与压力检测系统组成，如图1所示。循环流化床主体部分立管的横截面积为0.12m×0.70m，床高2.50m。床底材料为直径0.32mm的石英砂，密度为2 600kg/m3。压力脉动信号在距离布风板200mm处采集，采用Kistler7261型传感器，量程-5～5kPa，响应频率1Hz，采样频率400Hz，采样时间60s。

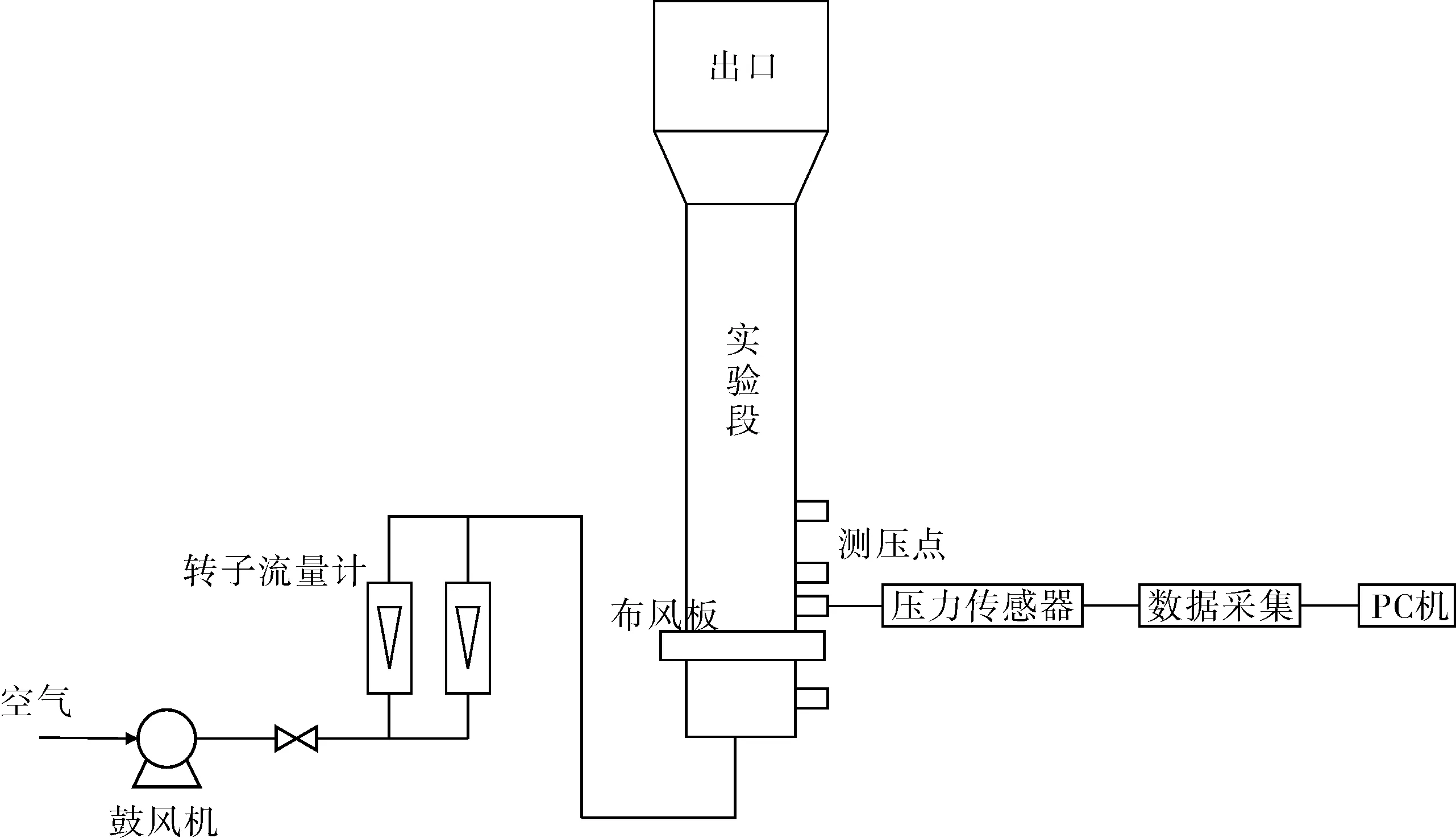
图1 流化床压力脉动实验装置示意图

实验过程中石英砂的总量保持不变，气相速度的变化范围在0.6～5.0m/s，随着气流速度的增加，在流化床依次观察到固定床、鼓泡流化床、湍流流化床和气力输送床4种流型，其对应的压力脉动信号如图2所示。在每种流化型态下，分别采样17段压力脉动时间序列，长度75 000，经过奈奎斯特频率低通滤波由计算机记录。

3 流化床流型的多尺度熵分析

不同工况下，固定床压力脉动信号多尺度熵的计算结果如图3所示，在尺度1～10，随着尺度的增加样本熵值近似呈线性增长，在第10个尺度后样本熵值基本保持不变；样本熵值在小尺度上对流动工况的变化不太敏感。分析其原因，在固定床流型下，气体主要从固体颗粒间的缝隙中通过流化床，粒子的搅动由气体射流，粒子搅动的运动规则毫无规律或者是混沌的，压力脉动信号反映的是整体行为，脉动幅度相对较小，夹杂着较多的周期性成分。

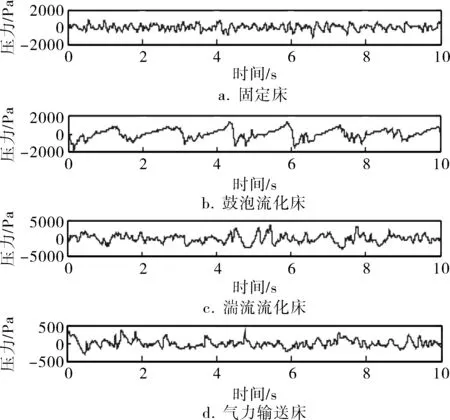
图2 压力脉动信号的时间序列

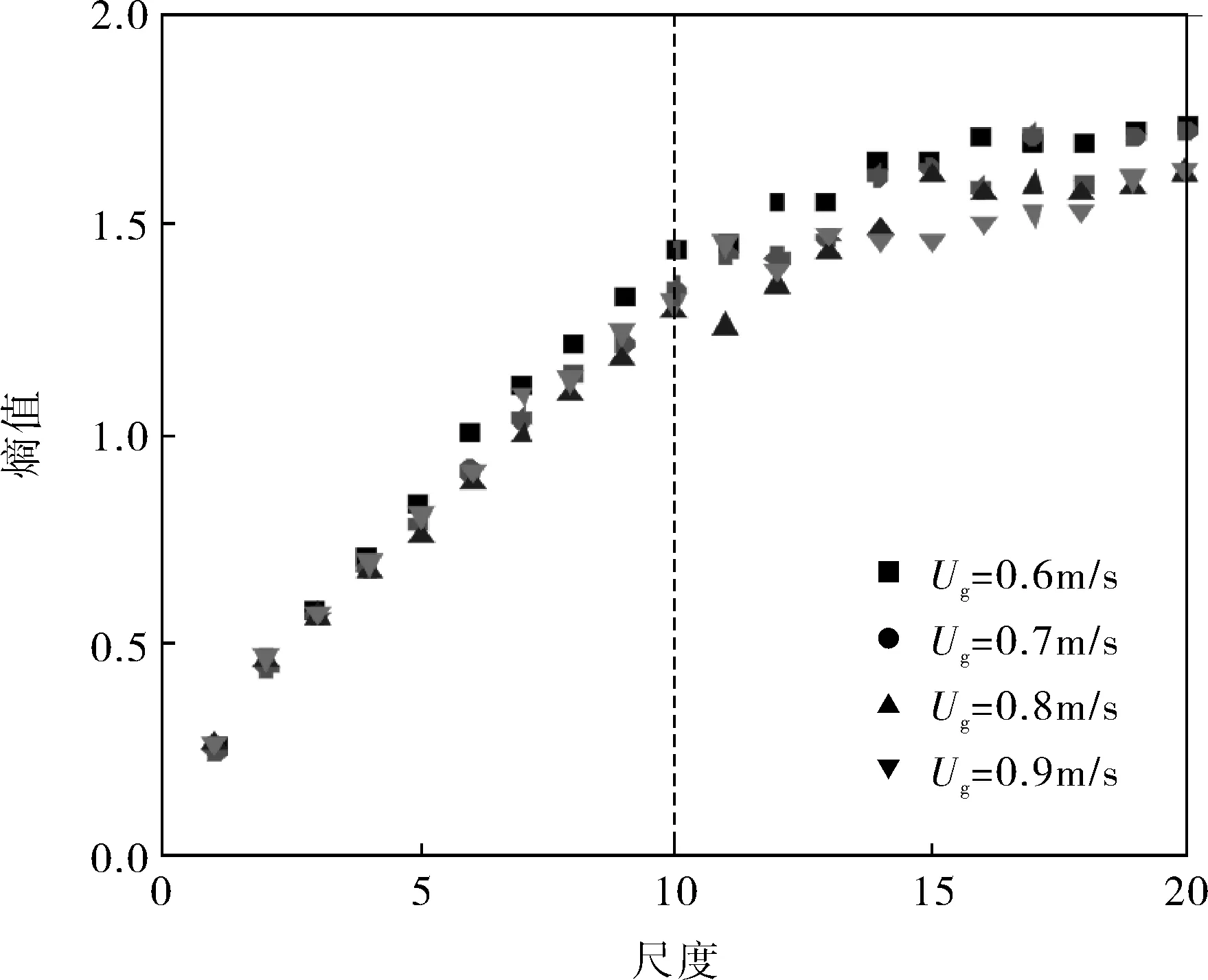
图3 不同工况下固定床多尺度熵特性

不同工况下，鼓泡流化床压力脉动信号多尺度熵的计算结果如图4所示，在尺度1～6，随着尺度的增加样本熵值近似呈线性增大趋势，且样本熵值对工况的变化不敏感；尺度8后，每种工况的样本熵值增长缓慢，且样本熵值对工况的变化十分敏感。这是因为在鼓泡床流化型态下，由于在流化床内产生明显的气泡，气泡引起的颗粒运动在床层运动中占主导作用，气泡的运动相对颗粒的搅动有规律得多，而随着气相速度的逐渐增大，气泡团聚并产生的大气泡在乳化相的剧烈扰动下破碎，大气泡量明显减少，床内的总体趋势表现为由鼓泡态的大尺寸、少量气泡的状态向小尺寸、多数量气泡的状态演变，床层慢慢进入湍流状态，压力脉动信号中随机分量迅速增强。

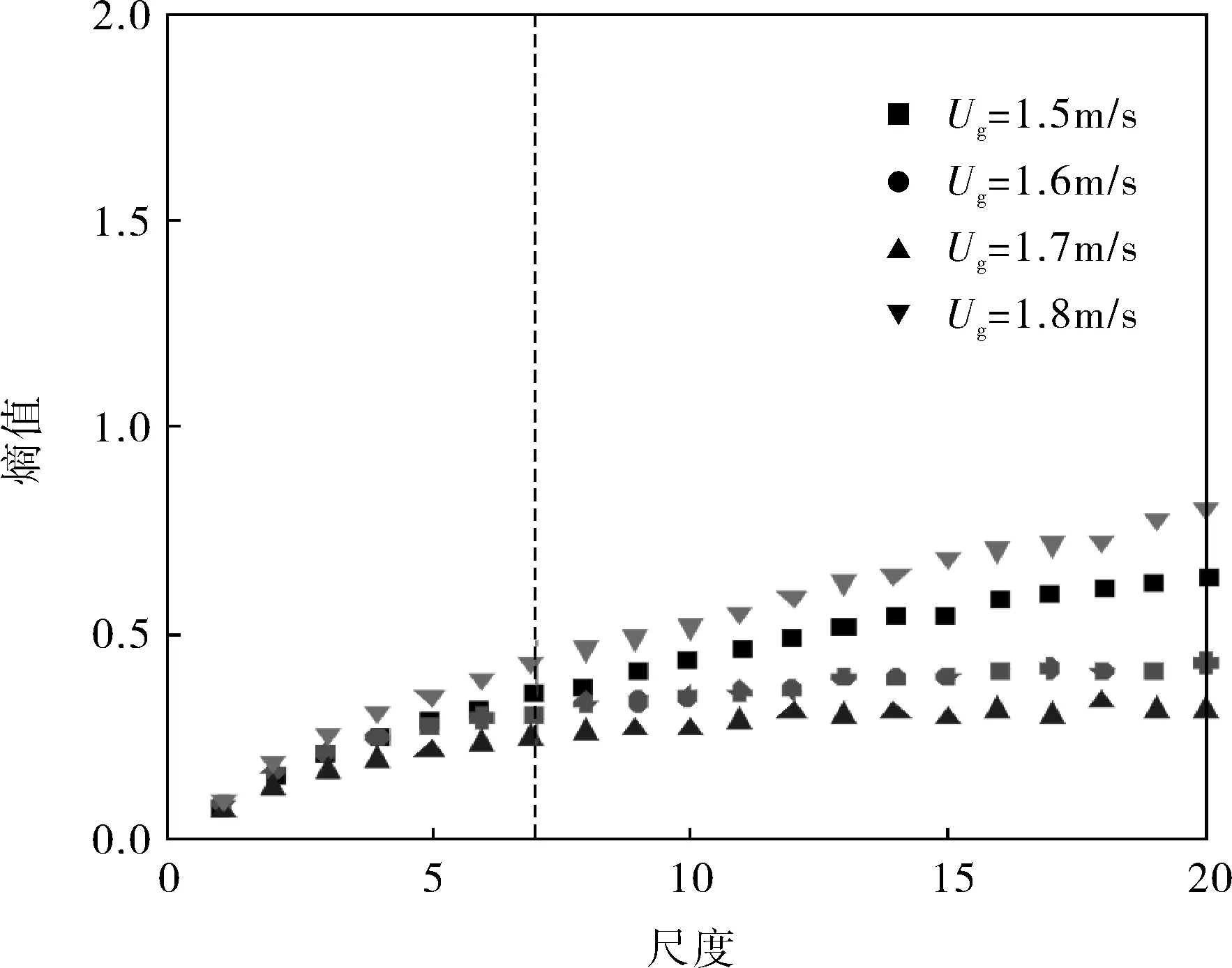
图4 不同工况下鼓泡流化床多尺度熵特性

不同工况下，湍流流化床压力脉动信号多尺度熵的计算结果如图5所示，在尺度1～12，随着尺度的增加样本熵值近似呈线性增长；在尺度10后，样本熵值的增长十分缓慢，而且在大尺度上样本熵值对流动工况的变化比较敏感。这是由于在流化床湍流流态下，气泡破裂，床面不存在或很难区分；颗粒浓度随高度连续下降，需要一定的颗粒循环量来维持颗粒总量，床密度不依赖颗粒循环倍率。

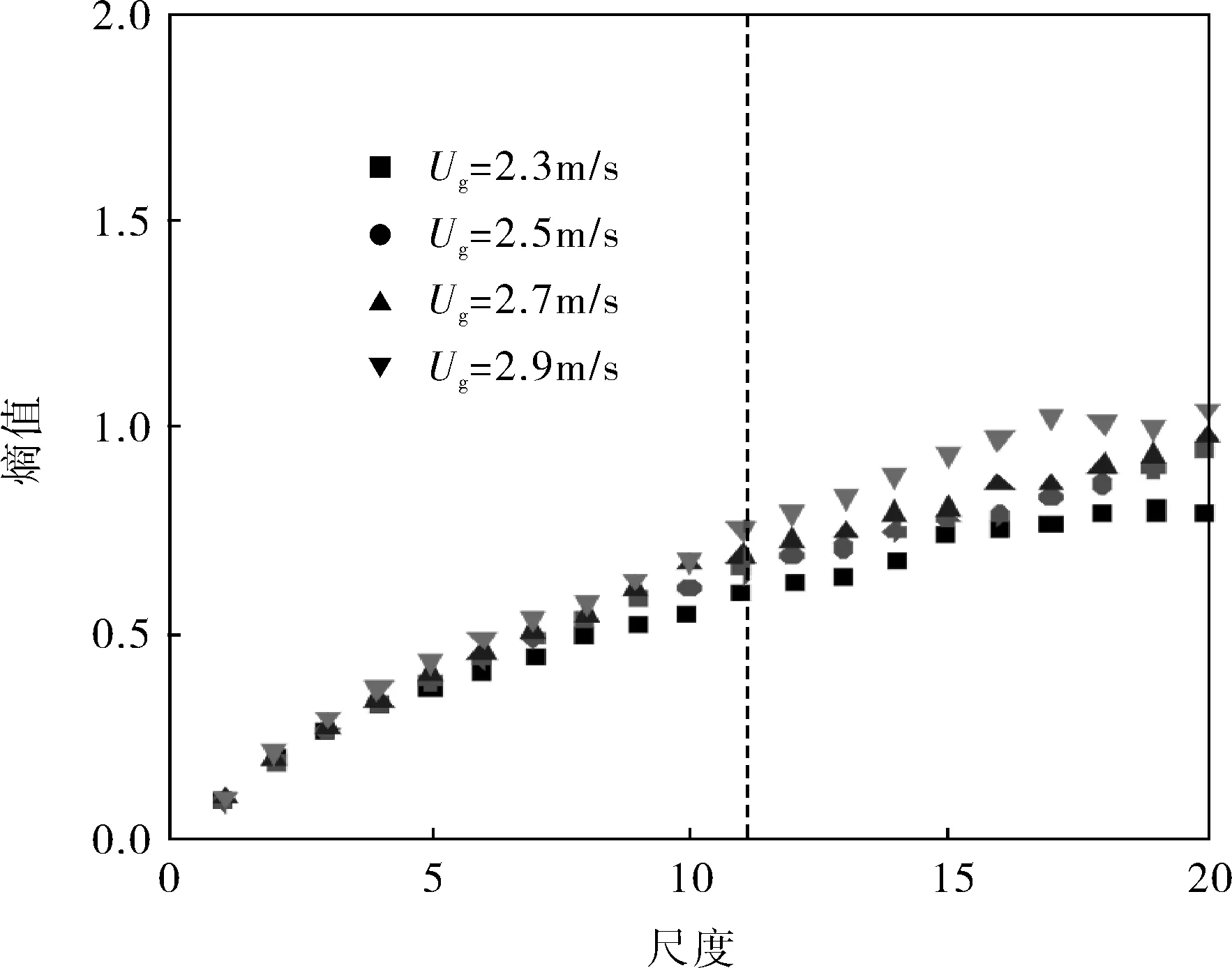
图5 不同工况下湍流流化床多尺度熵特性

不同工况下，气力输送床压力脉动信号多尺度熵的计算结果如图6所示，在尺度1～10，随着尺度的增加样本熵值增长趋势近似呈线性；在尺度10后，样本熵值对流动工况的变化较敏感，而且随着气相速度的增加，在相同尺度上样本熵值增大。这是由于颗粒在循环装置中相互碰撞或颗粒与壁面碰撞，颗粒随着气体的运动十分复杂，气相和颗粒处于混沌状态，压力脉动信号接近于固定床的压力脉动信号，脉动幅度相对最小，其内部还夹杂着较多的周期性成分。

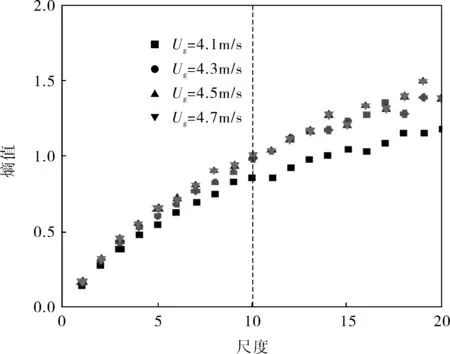
图6 不同工况下气力输送床多尺度熵特性

从图3～6可以看出，利用固定床压力脉动信号的多尺度熵特征分析可知，多尺度熵可以在不同尺度上很好地揭示固定床、鼓泡流化床、湍流流化床和气力输送床的动力学特性。样本熵值在小尺度上近似呈线性增长，不同流型样本熵值的增长速率有很大差异，同一流型的样本熵值增长速率差别不大。可以利用这一显著特征作为区分流型的新标准。样本熵值的增长速率在熵值曲线上就是曲线的斜率，可以通过最小二乘法拟合得到。笔者将其定义为多尺度熵率(Rate of MSE)。

不同流动工况下的多尺度熵率分布情况如图7所示，4种流型的多尺度熵率差别显著，其中固定床的多尺度熵率0.100～0.150，鼓泡流化床的多尺度熵基本位于0.045以下，湍流流化床的多尺度熵率在0.050～0.070，气力输送床的多尺度熵基本在0.070～0.100。

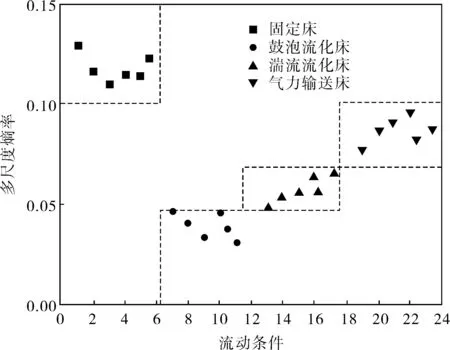
图7 不同流动条件下的流型辨识

4 结束语

多尺度熵作为一种非线性分析方法可以在多个尺度上表征信号的复杂性，并且对序列长度有较好的鲁棒性。笔者将多尺度熵分析应用到气-固两相流压力脉动信号分析中，揭示了流化床不同流型内部的动力学特性，并进一步揭示了不同流型之间的动力学差异。此外，在小尺度下4种流化型态的多尺度熵值都是随着尺度的增加近似呈线性增长，在大尺度下熵值的增长十分缓慢。在流化床气-固两相流不同流型多尺度熵表现出的不同变化趋势基础上，提出了一个新的参数——多尺度熵率，能较好地区分4种典型流型，为流化床气-固两相流流型辨识提供了新方法。

[1] Li J H,Mooson K.Particle-Fluid Two-phase Flow-the Energy-Minimization Multi-Scale Method[M].Beijing:Metallurgical Industry Press,1994.

[2] Zhao G B,Chen J Z,Yang Y R.Predictive Model and Deterministic Mechanism in a Bubbling Fluidized Bed[J].AIChE J,2001,47(7):1524～1532.

[3] Fan L T,Neogi D,Yashima M,et al.Stochastic Analysis of a Three-phase Fluidized Bed:Fractal Approach[J].AIChE J,1990,36(10):1529～1535.

[4] Franca F,Acikgoz M,Lahey R T,et al.The Use of Fractal Techniques for Flow Regime Identification[J].Int J Multiphase Flow,1991,17(4):545～552.

[5] 赵明阳,黄志尧,王保良,等.气固流化床压力波动信号的高阶统计量特性研究[J].仪器仪表学报,2001,22(z2)：11～12.

[6] 秦伟刚,王超,张文彪,等.气-固两相流差压信号的EMD和三阶累积量分析[J].仪器仪表学报,2014,35(4):762～767.

[7] 王春华,仲兆平,鄂加强.气-固流化床压力脉动信号分形标度分析[J].中国电机工程学报,2010,30(8):45～49.

[8] 张少峰,王琦,高川博,等.液固两相外循环流化床压力波动信号的统计及频谱分析[J].过程工程学报,2006,6(6):878～883.

[9] Zhu L,Jin N D,Gao Z K,et al.Multi-scale Cross Entropy Analysis for Inclined Oil-water Two-phase Countercurrent Flow Patterns[J].Chemical Engineering Science,2011,66(23):6099～6108.

[10] 郑桂波,金宁德.两相流流型多尺度熵及动力学特性分析[J].物理学报,2009,58(7):4485～4492.