端口受控哈密顿方法的永磁同步电动机弱磁扩速

王子函，于海生

(青岛大学，青岛266071)

0 引 言

交流永磁同步电动机没有换向装置和励磁绕组，因而具有结构简单、可靠性高、单位质量功率密度大、效率高等优点，所以在高精度的速度和伺服系统中得到了广泛的应用［1－3］。许多应用场合不仅要求系统在低速时具有较大的转矩输出，从而能够使系统快速起动、加速，而且还能够在电机达到额定电压和额定电流的情况下能够进一步提高电机的转速。近年来，弱磁扩速得到中外学者的广泛关注，并且取得了许多理论成果［4－6］。文献［4］提出了一种梯度下降法，但是该方法计算复杂，难以在实际中得到推广。文献［5］利用查表法实现系统的快速响应，但是该方法对数据表的精度要求很高，难以实现。文献［6］提出了一种考虑谐波的电压大小和相位的方法，但是该方法的速度响应慢。

近年来，非线性控制方法受到越来越多的关注，永磁同步电动机的非线性控制应用也越来越广泛。一种基于系统能量成形的端口受控哈密顿控制方法得到中外学者的广泛关注［7－8］，端口受控哈密顿系统具有结构简单、控制器的求取比较方便、稳态误差小、响应快速等优点，因而具有一定的实用价值。目前采用非线性方法控制永磁同步电动机的弱磁调速很少，而采用基于能量的哈密顿非线性控制方法几乎没有。本文提出了一种基于能量的端口受控哈密顿(PCH)的非线性控制新方法控制隐极永磁同步电动机的弱磁扩速。实际工程中，负载转矩并不是恒定不变的，针对这一问题设计了系统的负载转矩观测器。仿真结果表明，系统的弱磁扩速效果良好、响应速度快、稳态误差小，具有良好的抑制负载扰动能力。

1 永磁同步电动机PCH 系统模型

永磁同步电动机在d，q 坐标系下的速度数学模型可表示:

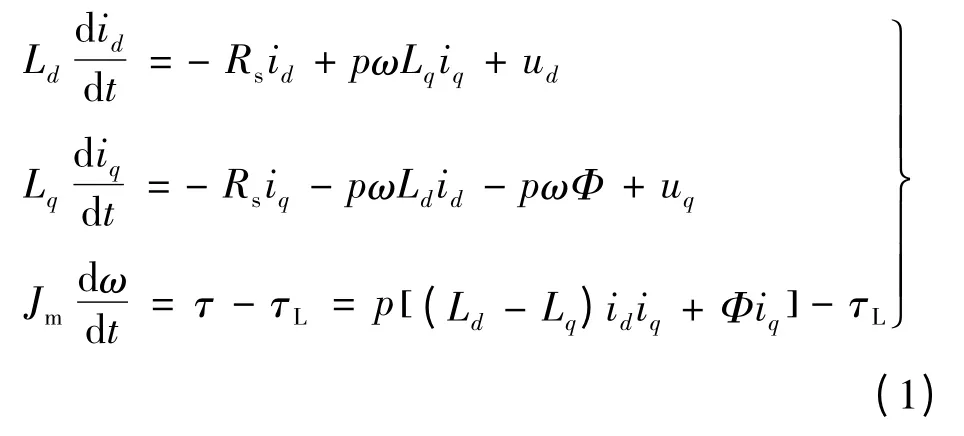
式中:ud，uq分别为d 轴、q 轴定子电压;id，iq分别为d 轴、q 轴定子电流;Jm为转动惯量;τ 为电磁转矩;Ld，Lq分别为d 轴、q 轴定子电感;τL为负载转矩;Φ为永磁体产生的磁链;Rs为定子电阻;p 为电机的极对数;ω 为转子的机械角速度。

取永磁同步电动机系统的哈密顿函数:

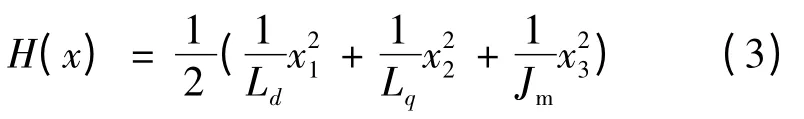
端口受控耗散哈密顿系统模型:

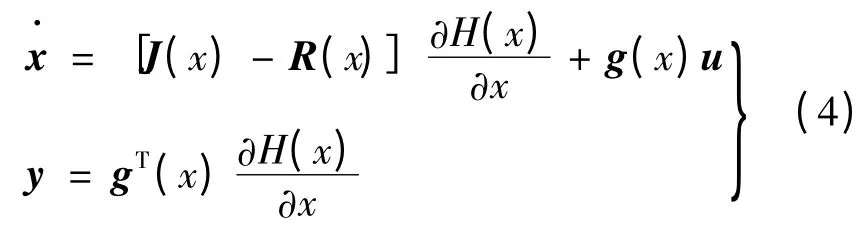
式中:x∈Rn，u，y∈Rn，R(x)为半正定对称矩阵，R(x)=RT(x)≥0;J(x)为反对称矩阵，J(x)=－JT(x)。将式(1)写成式(5)的形式，可得永磁同步电动机的PCH 模型:

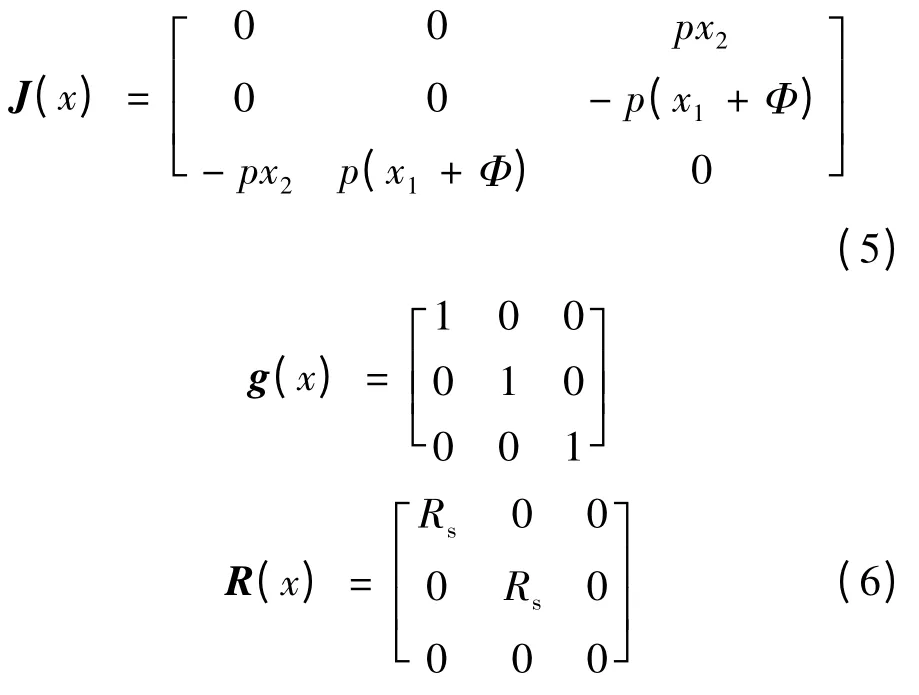
2 永磁同步电动机的PCH 弱磁控制原理

2.1 系统控制原理图

基于状态PCH 和弱磁扩速原理的永磁同步电动机速度控制系统的系统框图如图1 所示，其中ω0为给定转速，τL0为给定负载转矩。当给定转速在基速以下采用最大转矩/电流控制，求出系统的平衡点id0和iq0;当给定转速在基速以上采用弱磁控制，求出系统的平衡点［9］。

图1 控制系统原理框图

2.2 弱磁控制原理

针对隐极永磁同步电动机式(1)的前两个公式知，当永磁同步电动机达到稳态运行时，电压方程:

由于电机一般运行于较高转速，此时定子电阻可以忽略，可得到电压方程［10］:

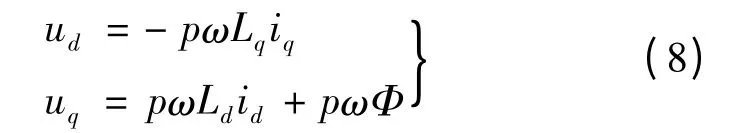
在交流调速系统逆变器容量足够大的条件下，当电机的端电压和电机的定子电流均达到额定值时，假设在dq 坐标系下电机的额定电压为ulim，额定电流为ilim，可以得到:

将式(8)代入式(10)可以得到电压极限椭圆:

由式(9)和式(11)可以得到电压极限椭圆与电流极限圆的轨迹，如图2 所示。

图2 隐极永磁同步电动机的定子电流轨迹

为了延长电机的使用寿命，电机的定子端电压和定子电流需要运行在电压极限椭圆轨迹和电流极限圆轨迹内。如图2 所示，A1点是电动机最大转矩/电流轨迹与电流极限圆轨迹的交点，电机的定子电流只能在电流极限圆内，A1点所对应的转折速度ω1就是电压极限椭圆轨迹与电流极限圆轨迹的交点。针对隐极永磁同步电动机，最大转矩/电流轨迹即q 轴如图2 中OA1段，在OA1段上电动机可以以每个点在转折速度以下(基速)作恒转矩运行，转折速度就是在该转矩下电压极限椭圆与最大转矩/电流轨迹的交点。图2 中的A1点是电机在输出最大转矩时能达到的最大转速。由于永磁同步电动机的励磁是永磁体产生的，所以要想继续提高电机的转速，只能通过调节定子电流来实现［11］。当电机运行在A1点时，要想继续提高电机的转速至ω3，可以让定子电流轨迹沿电流极限圆轨迹由A1点移动至B点，此时直轴去磁电流分量增大而交轴电流分量减小，从而使电机的气隙磁场减弱，提高了电机的转速。

2.3 弱磁控制策略

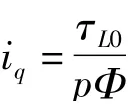
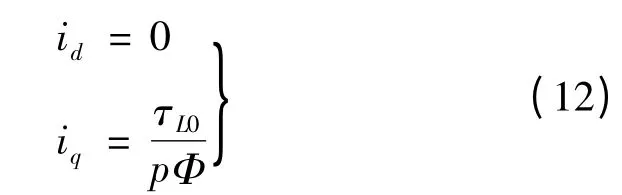
式中:τL0为负载转矩。将式(12)代入式(11)可得到转折速度:

电机在基速以上即ω ＞ωA时，采用弱磁控制［13］，此时，电压达到额定值，由式(11)、式(12)可以得到定子电流轨迹:

3 负载转矩恒定已知时控制器的求取

3.1 系统平衡点的确定

电机运行在基速以下即ω≤ωA，采用最大转矩/电流原理，由式(12)知系统平衡点:

电机运行在基速以上即ω ＞ωA时，采用弱磁控制，由式(14)、式(15)知系统平衡点:

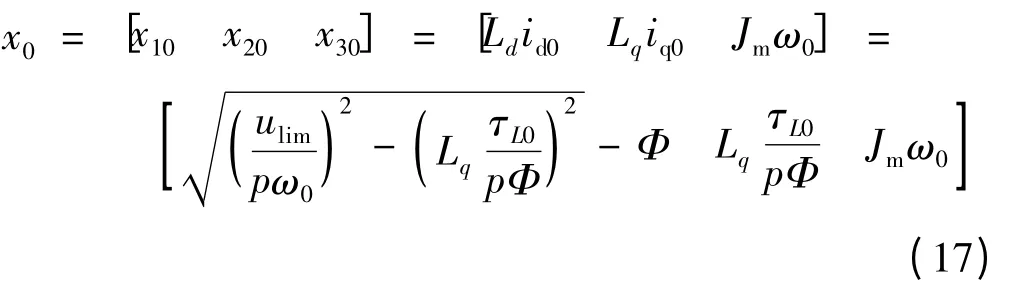
3.2 控制器的设计

取系统期望的哈密顿函数:

由状态PCH 理论［14］可以求出系统的控制器，

即:

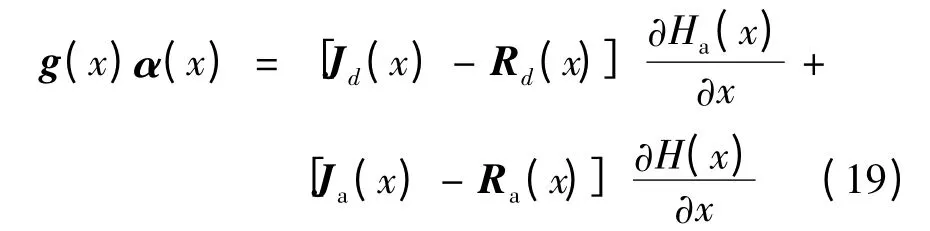
这里:

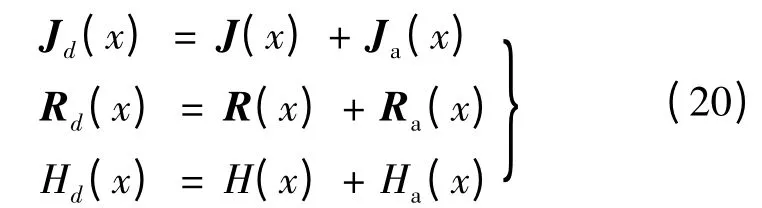
并且取:

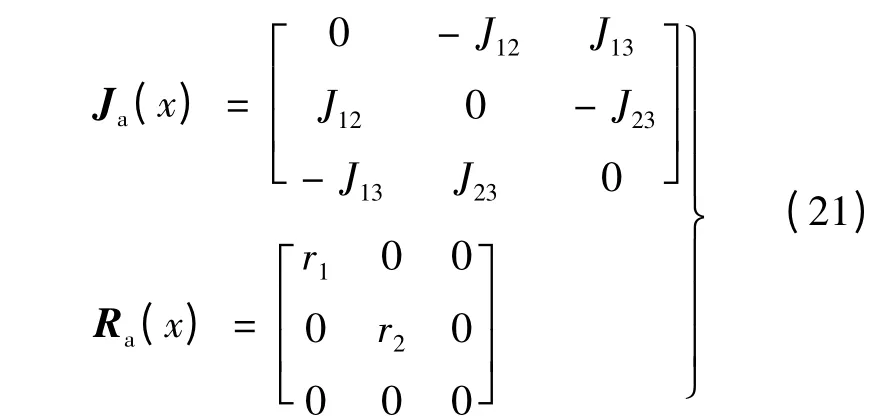
将式(3)、式(5)、式(6)、式(18)、式(20)、式(21)代入式(19)可得系统的控制器:

由式(4)和式(22)构成的系统是渐近稳定的［15］。

4 针对负载转矩未知时控制器的求取

4.1 负载转矩观测器的设计

在实际应用中，负载转矩通常情况下是不确定并且存在扰动的。为了解决这一问题，需要设计负载转矩观测器，当负载转矩恒定已知时，由式(1)、式(2)可得:

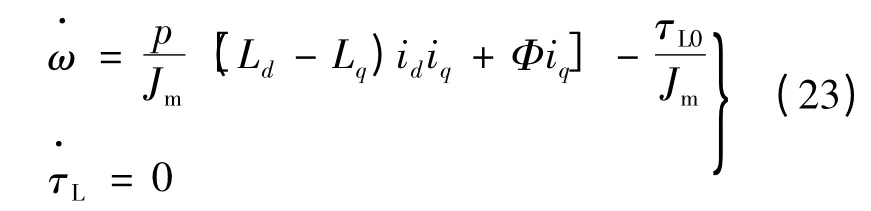
当负载转矩不确定时，根据误差反馈校正原理和式(23)可以得到负载转矩观测器:

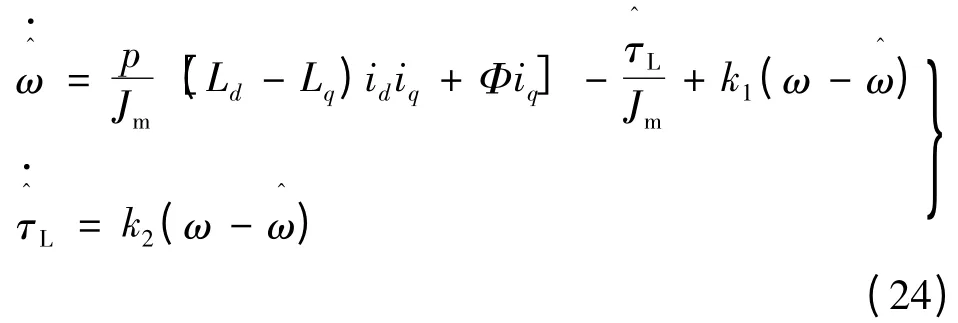
式中:k1，k2是设计参数为估计值。定义估计误差=ω－=τL－，由式(23)、式(24)可得观测器的跟踪误差动态方程:

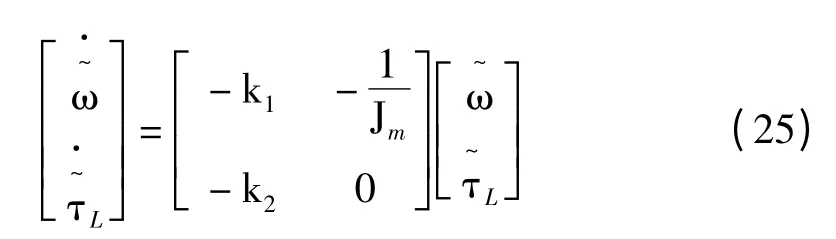
可以证明，选取适合的k1、k2可以确保观测器渐近稳定，经过配置极点能够得到良好的转矩估计的收敛速率。由式(25)可得观测器的极点:

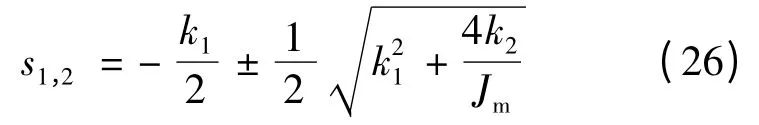
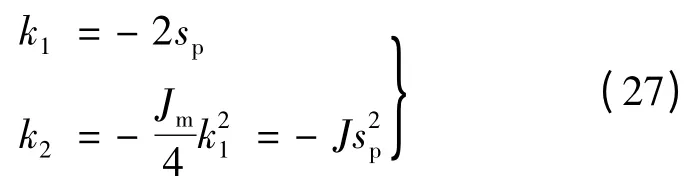
4.2 控制器的设计

式(29)是渐近稳定的［15］。

5 仿真结果

永磁同步电动机的参数:d 轴和q 轴定子电感Ld=Lq=0.008 5 H，永磁体磁通Φ =0.175 Wb，极对数4，定子电阻1.5 Ω，转动惯量J =0.001 1 kg·m2，额定电压150 V，额定电流4 A，额定转速150 rad/s，额定转矩4 N·m。

在MATLAB/Simulink 上进行仿真。

初始时刻给定转速120 rad/s，转矩1.5 N·m，在0.25 s 给系统一个0.5 N·m 的转矩扰动，在0.5 s 时给定转速400 rad/s，转矩0.5 N·m，在0.75 s给系统一个0.5 N·m 的负载转矩扰动。取控制器参数r1=r2=10，k=1，采用SVPWM 和IGBT 逆变器。

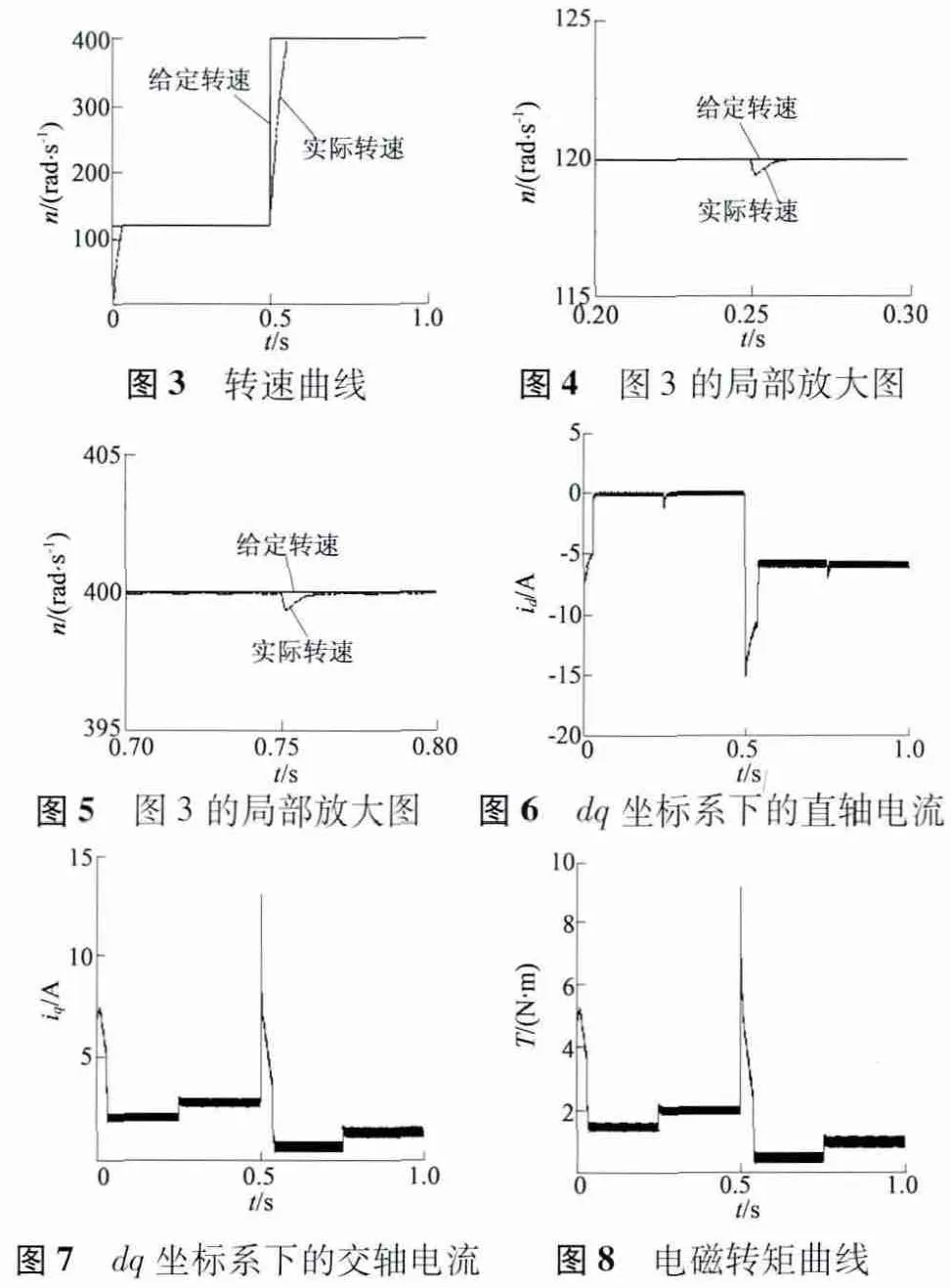
图3、图4、图5 是电机的转速曲线，在0 ～0.5 s，给定转速为120 rad/s，由于120 rad/s 小于基速，所以采用了最大转矩/电流的控制方法;在0.5 ～1 s，给定转速为400 rad/s，由于此转速大于基速，所以采用了弱磁控制方法。从图4、图5 可以看出，系统具有良好的抑制负载转矩扰动能力，并且能够快速到达给定位置，稳态误差小。图6、图7 是在dq坐标系下的直轴和交轴电流曲线，在0 ～0.5 s 内，直轴电流为零，采用了最大转矩/电流控制原理，在0.5 ～1 s 内，直轴电流的绝对值变大，为了使电流运行在电流极限圆内而减小交轴电流，以达到弱磁扩速的目的。图8 是电磁转矩曲线，在0 ～0.5 s 内，电机运行在基速以下，可以输出较大的电磁转矩，即可以带动较大的负载转矩，在0.5 ～1 s，电机运行在基速以上，为了使电机定子电流运行在电流极限圆内，必须减小交轴电流从而减小了电机的电磁转矩，即能带动较小的负载转矩。

6 结 语

本文应用端口受控哈密顿控制方法，研究了永磁同步电动机弱磁扩速问题。基速以下采用最大转矩/电流控制方法，实现了电机在低速时输出较大的电磁转矩;基速以上采用弱磁控制方法，可使电机在达到额定电流和额定电压情况下达到更高的转速。并且在负载转矩未知时设计了负载转矩观测器。仿真结果表明，基于端口受控哈密顿方法的弱磁调速系统具有良好的弱磁扩速性能，系统能够快速到达给定转速，稳态误差小，并且系统具有良好的抑制负载转矩扰动的能力。

［1］ LORIA A，ESPINOSA－PEREZ G，AVILA－BECERRIL S.Global adaptive linear control of the permanent magnet synchronous motor［J］.International Journal of Adaptive Control and Signal Processing，2014，28(10):971－986.

［2］ VIKAS K，PREMA G，MITTAL A P. ANN based self tuned PID like adaptive controler design for high performance PMSM position control［J］. Expert Systems with Applications，2014，41(17):7995－8002.

［3］ 王宏，于泳，徐殿国. 永磁同步电动机位置伺服系统［J］. 中国电机工程学报，2004，24(7):151－155.

［4］ 唐朝晖，丁强，喻寿益，等.内埋式永磁同步电机的弱磁控制策略［J］.电机与控制学报，2010，14(5):68－72.

［5］ BAE B，PATEL N，SCHUIZ S.New field weakening technique for achieving wide constant power speed operation with an interior PM alternator machine［C］//36th IEEE Industrial Application Society Annual Meeting.Chicago，USA，2001:807－814.

［6］ PAUL S，FABIEN M，XAVIER K.Control strategies for open－end winding drives operating in the flux－weakening region［J］.IEEE Transactions On Power Electronics，2014，29(9):4829－4842.

［7］ ORTEGA R，SCHAFTB A，MASCHKEC B，et al.Interconnection and damping assignment passivity－based control of port－controlled Hamiltonian systems［J］.Automatica，2002，(38):585－596.

［8］ YU Hai－sheng，YU Jin－peng，WU He－rong. Energy－shaping and integral control of the three－tank liquid level system［J］.Nonlinear Dyn，2013(73):2149－2156.

［9］ 唐任远.现代永磁电机［M］.北京:机械工业出版社，1997.

［10］ JIRI S，JAROSLAV N.FOC and flux weakening for traction drive with permanent magnet synchronous motor［J］.IEEE Transaction on Industrial Electronics，2008，3(2):753－758.

［11］ YUKINORI I，SHIGEO M，MASAYUKI S. Comparative study of PMSM drive systems Based on current control and direct torque control in flux－weakening control region［J］.IEEE Transactions On Industry Applications，2012，48(6):2382－2389.

［12］ 于海生，王海亮，赵克友.永磁同步电机的哈密顿系统建模与控制［J］.青岛大学学报，2005，20(3):3－6.

［13］ 唐朝晖，丁强，喻寿益，等. 表面贴装式永磁同步电机弱磁控制策略的研究［J］.控制工程，2011，18(3):384－387.

［14］ 刘旭东.基于无速度传感器的永磁同步电机PCH 控制［D］.青岛:青岛大学，2011:35－41.

［15］ 于海生，赵克友，郭雷，等.基于端口受控哈密顿方法的PMSM最大转矩/电流控制［J］.中国电机工程学报，2006，26(8):82－87.