三相盘式感应电动机定子磁场研究

2015-01-13上官璇峰

微特电机 2015年10期

上官璇峰，杨帅

(河南理工大学，焦作454000)

0 引言

盘式感应电动机又称轴向磁通感应电动机(以下简称AFIM)，与普通的径向磁场电机相比最大的不同是其磁场方向为轴向［1－3］。AFIM 磁场沿径向分布，随着半径和齿距的变化而呈现出一定的规律。

目前研究AFIM 常见的方法有平均半径法和分环法。平均半径法以整体为对象，忽略了磁场沿径向的分布规律;而分环法则以平均半径法为基础，通过对半径分环计算来呈现气隙磁密随半径的变化。文献大多采用分环法来设计和分析AFIM［4－6］，而在计算中发现分环法和三维有限元法的结果并不十分吻合。经分析其主要原因是分环法没有考虑到环与环之间的相互影响。虽然有一些文献在分环法的基础上也考虑了纵向、横向甚至轴向的一些边端效应［7］，但是却并未考虑环与环之间的边端效应影响。

本文分别采用解析法、分环法和三维有限元法求解气隙磁密，并绘出其基波幅值随半径变化的曲线。通过比较三种方法的计算结果，分析了其存在差异的原因，并在解析法的基础上提出了径向气隙系数。通过算例验证了该方法计算的结果和三维有限元法计算的结果基本吻合，可以正确地反映气隙磁密沿径向的变化规律。

1 解析法计算AFIM 气隙磁密

AFIM 与普通柱式电机磁路的最大不同在于其气隙磁密Bδ随半径r 是变化的［8］。

如果不计磁路铁心部分的磁压降，则气隙磁密的幅值:

式中:Fm为基波磁势幅值;Kc为气隙系数;δ 为气隙长度;μ0为真空磁导率。

1.1 基波磁势幅值Fm

在三相绕组中施加对称正序电流，在某一瞬时t距离A 相绕组轴线θs电角度处，三相合成基波磁动势［9－10］:

基波磁动势幅值:

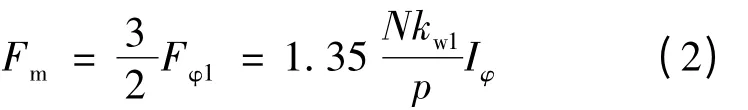
1.2 气隙系数Kc

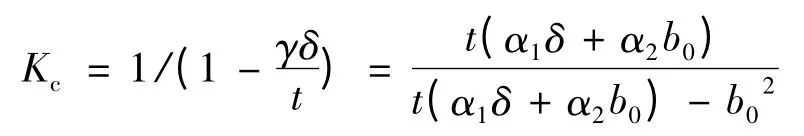
对于开口槽，α1=5.0，α2=1.0;

对于半闭口槽，α1=4.4，α2=0.75。

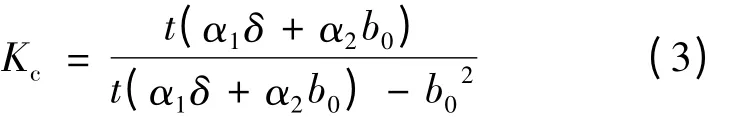
将式(2)、式(3)带入式(1)中，可得气隙磁密幅值Bδ:

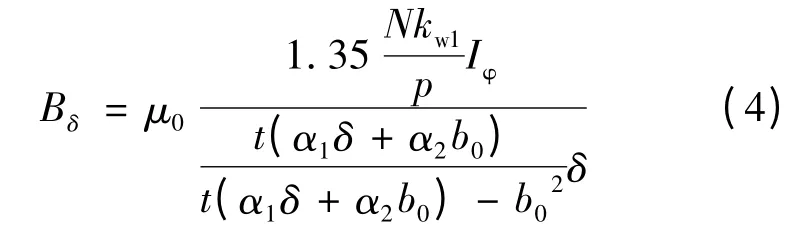
预先设计的三相AFIM 的参数如表1 所示。这里需要做如下说明:为准确研究电机的定子磁场而不受转子磁场的干扰，本文中所涉及电机在计算和仿真中均去除了转子铜盘。

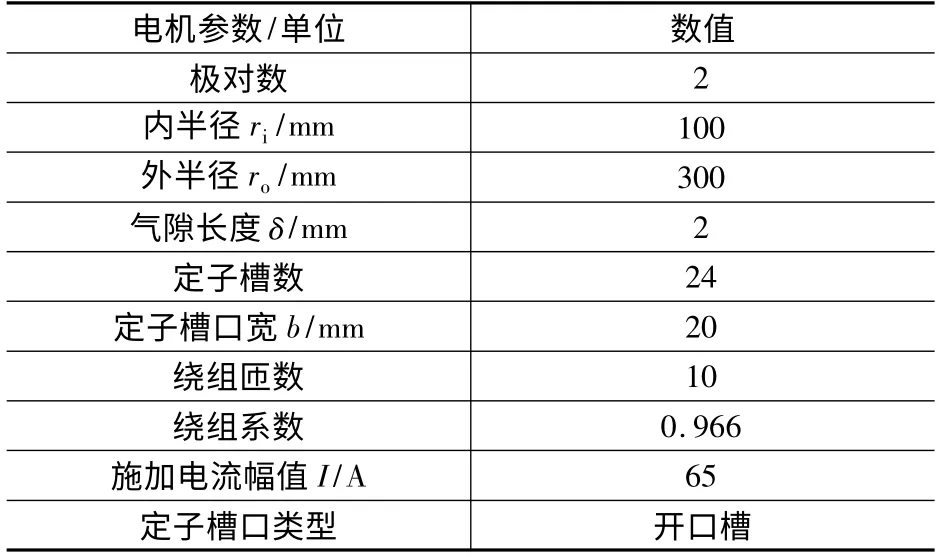
表1 半径100 ～300 mm 三相AFIM 参数

将表1 数据带代入式(3)和式(4)，并作如下假设:暂不考虑Ri，R0处的边端效应;半径r 在Ri，R0上磁路未达到饱和。则该电机气隙系数和气隙磁密随半径变化的函数:

绘出气隙系Kc和气隙磁密幅值Bδ随半径r 变化的曲线，如图1 和图2 所示。

图1 气隙系数Kc 随半径r 变化的曲线

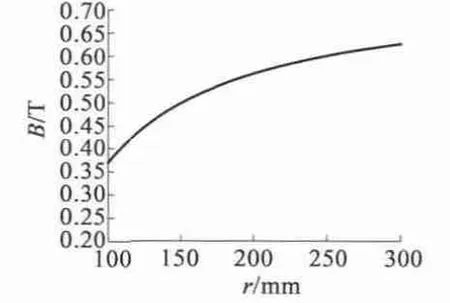
图2 气隙磁密幅值Bδ 随半径r 变化的曲线

由图1 和图2 可知，随着半径r 增加，气隙系数Kc减小，气隙磁密幅值Bδ增加。因此，在磁路不饱和情况下，气隙磁密幅值Bδ应随半径r 的增加而增加。

由气隙磁密幅值Bδ随半径的变化可得气隙磁密随半径r 在360°电角度上的三维变化，如图3 所示。

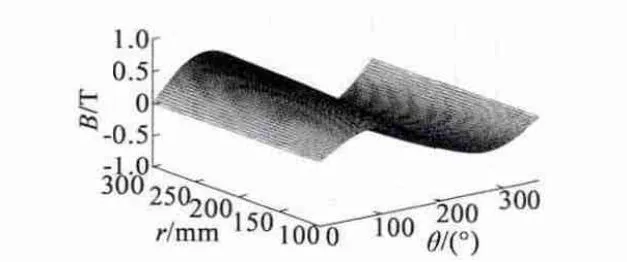
图3 气隙磁密随半径r 在360°电角度上的变化图

2 分环法计算AFIM 气隙磁密

1)根据预先设计的三相AFIM 相关参数，从内半径100 mm 到外半径300 mm 每隔25 mm 取一个半径值，则可取包括内外半径和平均半径在内的9个环，其在三维模型中的位置如图4 所示。

图4 9 个环在三维模型中的位置

2)考虑到盘式电动机定转子和气隙接触的两个面是互相平行的特征及磁路特点，与不考虑纵向边端效应的直线电动机更为一致，而且建模也更为简便，因此采用二维直线电动机模型来等效替换。则该环半径处的周长即为等效直线电动机的纵向长，而定子、转子和气隙厚度均不改变，齿槽形状尺寸也不改变，横向长度可取为25 mm。因为后续要施加电流源，而直线电动机又为二维模型，不考虑横向边缘效应，所以横向长度并不影响气隙磁密结果。为使等效前后一致，直线电动机还需要加纵向周期性边界条件来抵消断裂的影响。等效后的直线电动机模型如图5 所示。

图5 等效直线电机模型

3)对三相AFIM 施加对称三相电流则等效于对9 个直线电动机模型施加相同的三相对称电流。然后对直线电动机二维瞬态仿真至稳定状态。

4)分别对上述9 个直线电动机模型的气隙磁密进行傅里叶分解，获得各气隙磁密的基波幅值如图6 所示。

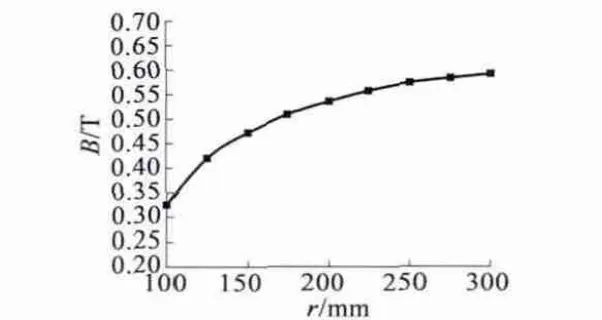
图6 9 个直线电动机的气隙磁密基波幅值

3 三维有限元法计算AFIM 气隙磁密

对三维模型施加幅值为65 A 的三相对称电流，进行三维瞬态仿真至稳定状态。由于施加边界条件故不存在内外半径处边端漏磁现象。分别对上述9个环所在三维模型位置处的气隙磁密进行傅立叶分解，获得各环气隙磁密的基波幅值如图7 所示。

图7 9 个环处的气隙磁密基波幅值

4 解析法、分环法与三维有限元法结果的比较与分析

分别将通过解析法、分环法和三维有限元法得到的气隙磁密基波幅值曲线进行比较，如图8 所示。

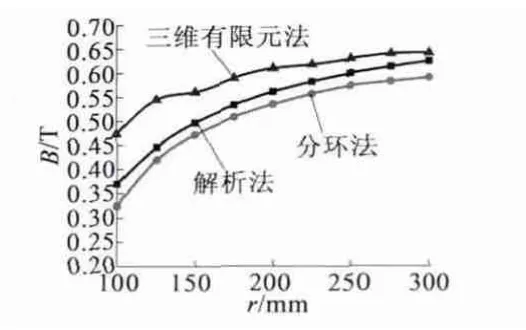
图8 解析法、分环法和三维有限元法的气隙磁密基波幅值比较

由图8 可知，在磁路不饱和情况下，三相AFIM气隙磁密基波幅值随半径增大而呈现增大的变化趋势;解析法和分环法在变化趋势和结果上基本一致，但和三维有限元法计算的结果却存在一定的差异。在半径较小处，三维有限元法计算的气隙磁密基波幅值大于解析法和分环法计算的气隙磁密基波幅值。

这种现象是因为解析法和分环法都是基于某个半径或某个环的孤立分析，没有考虑和相邻半径或环之间存在的径向边端效应;而三维有限元法则是基于整个模型的分析，将这种径向边端效应考虑在内。这种径向边端效应使气隙磁密出现了由高向低的传递，从而气隙磁密基波幅值原本高的就变得稍低，而低的又会变得稍高，类似于一种中和的现象。因此三维有限元法得到的气隙磁密基波幅值曲线就会比解析法和分环法得到的气隙磁密基波幅值曲线要平缓一些。我们把这种气隙磁密沿径向重新分布的现象归纳为径向气隙系数k 的影响。

5 径向气隙系数k 的探究

5.1 分析归纳

影响三相AFIM 气隙磁密分布的首要因素是半径，而半径的变化又引起了气隙系数的变化，因此可以通过解析法计算出每个位置的气隙磁密基波幅值。解析法只是孤立的考虑每个半径值对应的气隙磁密基波幅值，而并没有考虑到相邻半径的磁路之间的相互影响，即没有考虑到径向边端效应。径向边端效应存在的原因是相邻半径处的磁通和磁通密度不同。径向边端效应的强弱跟磁通密度的变化率有关，也就是和气隙系数Kc的变化率有关。径向气隙系数k 就是径向边端效应强弱的反映，与一般的气隙系数相对应称作径向气隙系数。

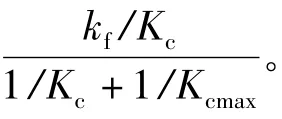
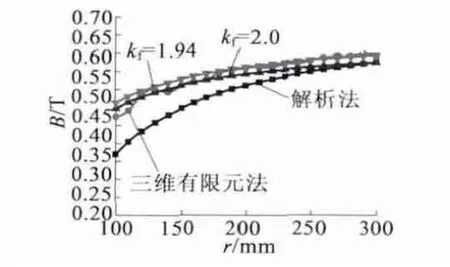
图9 kf =2.0 和kf =1.94 时气隙磁密基波幅值与解析法和三维有限元法结果的比较

5.2 验证径向气隙系数k 的准确性

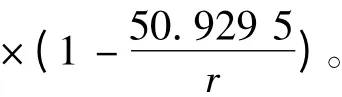
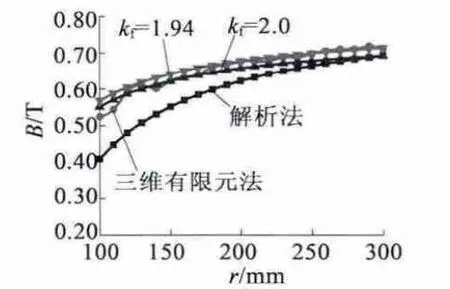
图10 kf =2.0 和kf =1.94 时气隙磁密基波幅值与解析法和三维有限元法结果的比较

另设计半径150 ～300 mm 盘式电机，其具体参数如表2 所示。

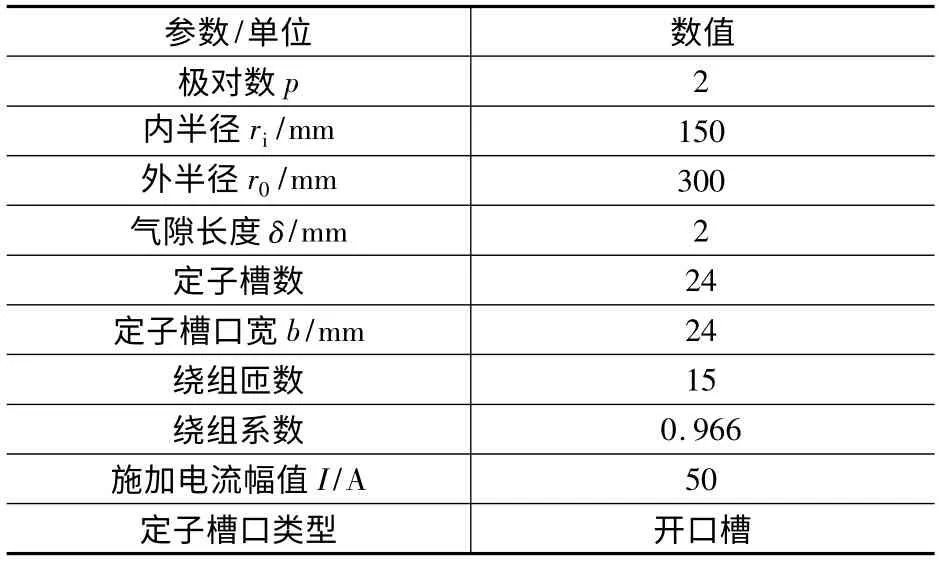
表2 半径150 ～300 mm 三相AFIM 参数

对应气隙磁密幅值Bδ的表达式:

同上例的方法，得到三维有限元法的结果。通过径向气隙系数k 计算得到的气隙磁密基波幅值与解析法和三维有限元法结果的比较，如图11 所示。

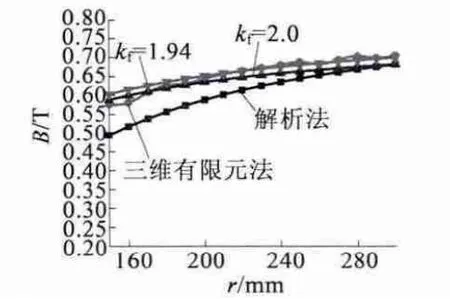
图11 kf =2.0 和kf =1.94 时气隙磁密基波幅值与解析法和三维有限元法结果的比较

由图10 和图11 可知，当kf取较大值时在内半径到平均半径范围内得到的气隙磁密基波幅值曲线和三维有限元法的气隙磁密基波幅值曲线吻合较好;当kf取较小值时在平均半径到外半径范围内得到的气隙磁密基波幅值曲线和三维有限元法的气隙磁密基波幅值吻合较好。但两者结果相差很小，可根据设计和分析需要在1.9 ～2.0 范围内取kf值，基本可以满足要求。