一种基于矢量控制的异步电动机节能策略

胡福年，林宗浩，孙守娟

(江苏师范大学，徐州221116)

0 引 言

异步电动机的电能消耗量约占全国工业用电量的60%以上［1－2］，交流异步电动机在实际运行中，由于负载特性，可能经常会处于轻载(或空载)状态，致使异步电动机的功率因数低，效率不高［3－4］。

近年来，国内外开展了许多关于异步电动机降损节能的研究。降损节能的方法主要有两大类，一类是优化电动机结构和制造工艺来提高电动机本身的效率，这适用于电动机的设计生产制造阶段［5］，在电动机运行时无法对损耗进行控制［6］。另一类是在电动机调速运行的过程中，通过合理有效的控制方法减少电动机的运行损耗，提高运行效率。对变频调速的异步电动机节能降损的控制方法主要有损耗模型控制、在线搜索控制［7］以及混合搜索控制。但是无论采取何种控制策略，电机在轻载运行时其磁通都将降低，为了保证矢量控制下的异步电动机转矩的高动态性能，节能控制过程仅在电动机处于稳态时才有效［5，9，16］，且节能控制一般适用于电动机的轻载工况［8］。文献［9］建立了异步电动机损耗模型，分析了异步电动机在不同负载转矩、转速下损耗与转子磁通之间的关系，并提出了调节转子磁链实现异步电动机的降损节能。文献［10］给出了电动机总损耗与定子磁链的关系式，在一定运行工况于异步电动机调速控制方法主要有调压调速、变压变频调速、矢量控制变频调速等。目前基于矢量控制下求得最小损耗时的定子磁链，文献［11］给出了异步电动机效率最高时，励磁电流iM1和转矩电流iT1的最优分配策略。以上分析都是基于损耗模型的控制方法。文献［12］在线搜索损耗功率最小的定子磁链值，文献［13］基于遗传算法在线搜索损耗最小时的转子磁链，并将此转子磁链作为矢量控制转子磁链给定值，达到降损节能的目的。文献［14］运用了模糊寻优控制，自适应减少isd以降低转子磁链。以上都为在线搜索控制方法。文献［15］采用了基于黄金分割法的混合搜索，搜索损耗功率最小时的转子磁链来提高效率。文献［16］提出了一种结合模糊搜索和黄金分割法的混合搜索方法，在线搜索转子磁链以达到节能的目的。根据上述分析，对于损耗模型控制，其最优给定值直接由计算得到，响应速度快，但受电动机参数变化的影响较大;对于在线搜索控制，它在一定程度上解决了电动机参数变化对节能控制的影响，但算法的收敛时间较长;混合搜索控制则结合了以上两种方法的优点，在一定程度上解决参数变化对控制精度的影响和算法收敛时间较长的问题，但当电动机输出转矩发生改变时，需重启搜索算法。

本文通过分析电动机的损耗模型发现，一定工况下电动机损耗最低时定子电流isq与isd的比值不随电动机的电磁转矩变化而改变，由于这种关系，本文提出了一种基于黄金分割算法的混合搜索节能控制方法。该搜索方法将传统以输入功率最小为搜索目标，不断调整异步电动机转子磁链的搜索方式改为不断调整异步电动机定子电流isq与isd的比值，使电动机输入功率达到最小，损耗最低。由于该最优比值与电动机的转矩无关，所以当转矩变化时该比值不变，无需重启搜索算法，这样可以减少搜索次数以减少搜索时间和搜索过程中电动机的转矩脉动。

1 异步电动机节能运行分析

1.1 异步电动机损耗模型

异步电动机的损耗可分为定子铜耗、定子铁耗和转子铜耗、转子铁耗［17］。异步电动机按转子磁场定向含铁耗的稳态等效电路［18］如图1 所示。为简化其数学模型，图1 忽略了定转子漏感，铁心损耗用等效电阻RFe的损耗来表示，另外由于转子铁损相对于定子铁损较小，所以通常情况下忽略转子铁耗［9］，因此忽略不计。

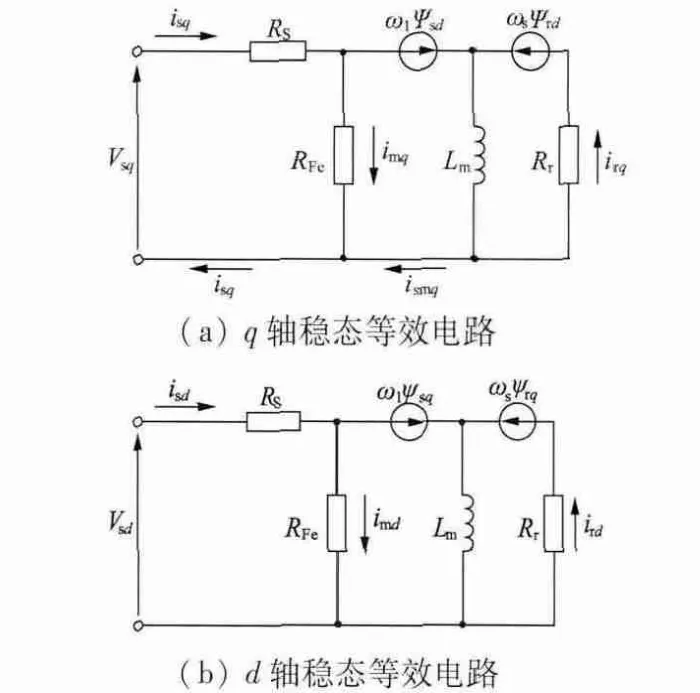
图1 异步电动机稳态等效电路

由于在按转子磁场定向的同步旋转坐标系中，d－q 轴电流为直流，所以图1 中电感两端的感应电压为零［9］。由于按转子磁场定向，所以可得:

式中:ψsd为定子d 轴磁链;ψrd为转子d 轴磁链;ψr为转子磁链;ψsq为定子q 轴磁链;ψrq为转子q 轴磁链。再由电机磁链方程可得:

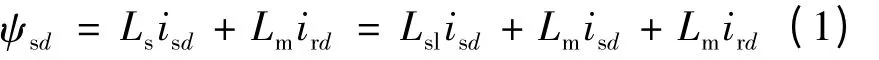
式中:Ls为定子电感;Lm为互感;Lsl为定子漏感;ird为转子d 轴电流。忽略Lsl，且稳态下ird=0，所以式(1)可以写成:

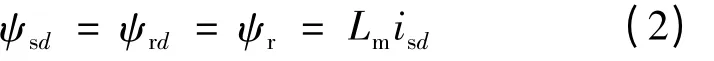
由图1(a)可知:

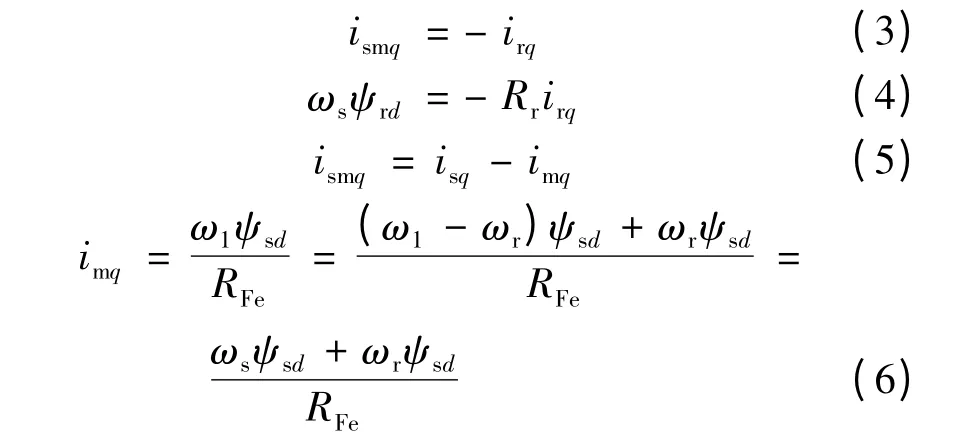
联立式(2)～式(6)可得:

即:

异步电动机的损耗由定子铜耗、定子铁耗和转子铜耗组成。

定子铜耗:

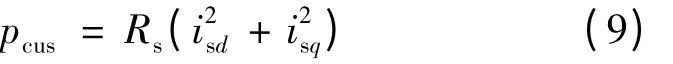
定子铁耗:

转子铜耗:

总损耗:

联立式(3)、式(5)、式(8)～式(12)可得:

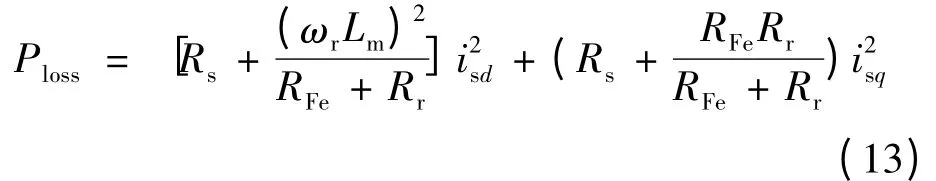
令

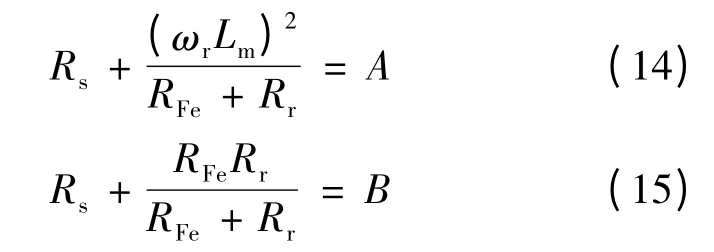
将式(14)～式(15)代入式(13)可得:

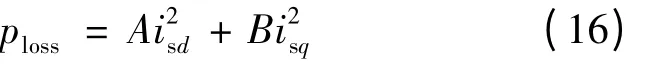
由上式可知，异步电动机总损耗与定子电流isd，isq的大小有关。也就是说在保证满足工作条件的情况下，可以控制定子电流isd，isq，使得总损耗降到最小。

1.2 损耗模型的优化计算

为了实现异步电动机节能控制，磁链的大小要根据当前的负载和转速来进行调节。当异步电动机在轻载弱磁区工作时，突然加速或转矩变大，为了提高系统的响应速度，磁链要恢复额定值以满足转矩要求，所以效率控制一般仅在稳态时进行。矢量控制中，电动机电磁转矩可以写成下式:

式中:Te为电磁转矩;p 为极对数。

构造目标函数:

列出下列偏导数:

联立式(19)～式(21)，可求得isq与isd比值的最优值，即:

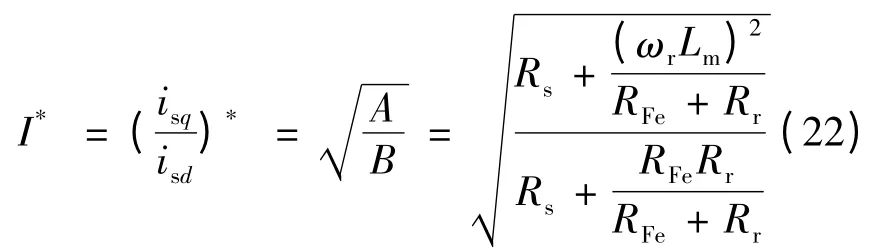
该最优比值只与电动机参数和转速有关，和电动机的电磁转矩Te无关，所以当电动机恒速运行时，当电磁转矩改变，该最优比值保持不变。

2 最小损耗运行点在线搜索

这里引入基于黄金分割算法的在线搜索法，本文主要以保持输出功率一定为前提，即稳态时电动机输出转矩和转速保持不变，不断调整isq，isd的分配比例，同时检测输入功率，输入功率最小时，损耗最低。其流程图如图2 所示。

第一步:由式(19)确定电流最优比值I*，并以［I*－0.5 I*+0.5］为搜索区间;

第二步:按照黄金分割算法的规则，插入两个搜索比例值I1和I2，并测量出当比例值为I1时系统的输入功率Pin(I1)和为I2时系统的输入功率Pin(I2);

第三步:根据这两个点的功率值，作出判断:

(1)如果Pin(I1)≥Pin(I2)，则缩小搜索区间为［I1，b］，同时在此区间确定下一个搜索点;

(2)如果Pin(I1)＜Pin(I2)，则缩小搜索区间为［a，I2］，同时在此区间确定下一个搜索点。

之后的过程与此相同，直到搜索区间长度小于一给定值ε，退出搜索，取区间中点值为最优比例值。

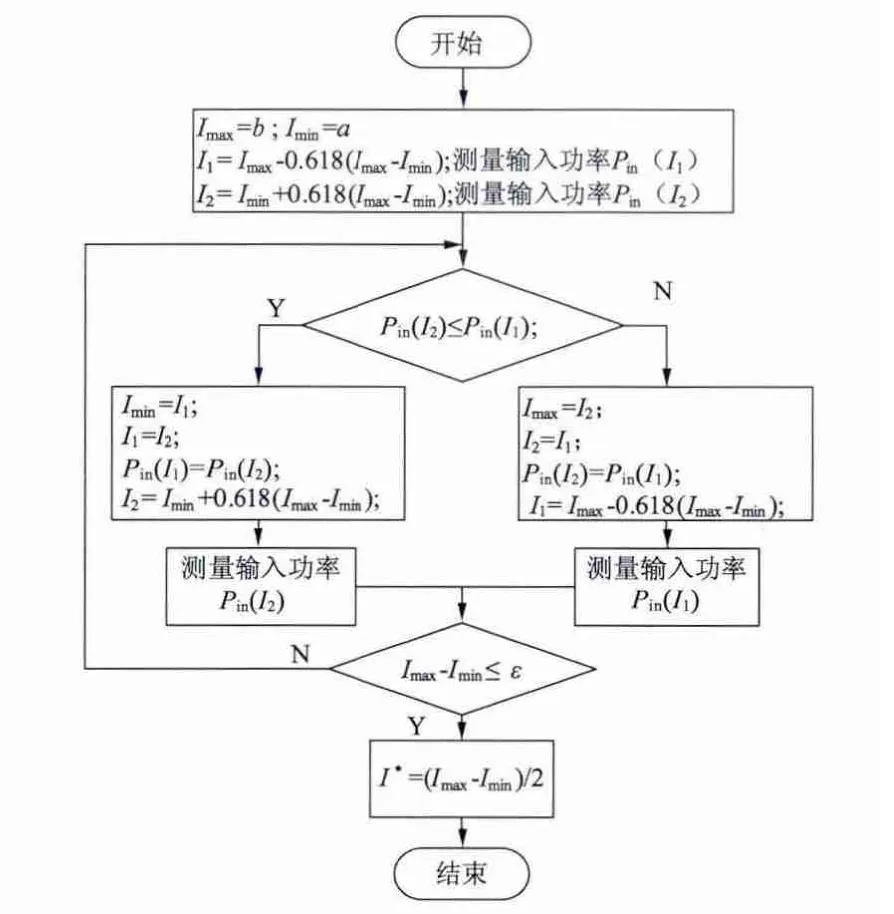
图2 基于黄金分割法最佳运行点搜索流程

3 实验系统设计

针对以上的节能控制策略，本文设计实验验证系统。实验系统采用以DSP 为控制核心的硬件设计方案，系统主要由主电路模块、控制模块和检测模块组成。PC 作为上位机与DSP 通过RS－232 接口实现通讯，并且在PC 机上观察运行结果。当系统进入节能控制过程时，DSP 根据电动机运行时的输入功率来调节isq，isd的分配比例。DSP 对采样获得的电流、转速等信息进行计算，获得电机的转速和位置，并计算得到PWM 控制信号，PWM 控制信号经过光耦隔离驱动IPM 模块。当系统出现短路、过流、过压等故障时，故障信号经光耦隔离送到DSP的PDPINTx 引脚，封锁PWM 的输出，使电动机停转。系统硬件结构框图如图3 所示。

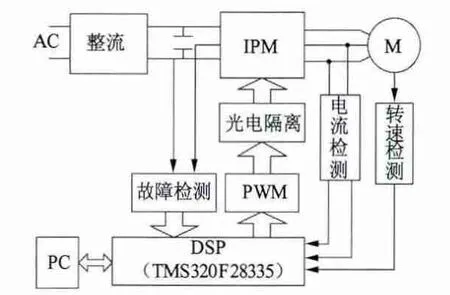
图3 系统硬件结构框图

3.1 主电路模块

本文的实验系统的主电路模块是由整流电路、滤波电路、逆变电路组成的AC－DC－AC 变频电路。逆变部分采用智能功率模块IPM。本文的IPM采用富士的6MBP75RA060，其最高工作电压为600 V，最大工作电流为75 A，开关频率为20 kHz。此型号的IPM 其内部集成了6 个IGBT，PWM 信号经光电隔离电路输入到其控制脚。IPM 模块内部包含短路保护(SC)、过流保护(OC)、过热保护(OH)、控制电源欠压保护(UV)等内置保护电路。

3.2 控制与检测模块

3.2.1 DSP 的选用

本系统由于采用矢量控制策略，且还需要进行搜索节能控制，所以数据计算的工作量很大，对精度的要求较高，同时为了保证节能控制的实时性，还要求DSP 的计算速度快，所以本系统采用了TI 公司新推出的一款浮点型数字信号处理器TMS320F28335，它在原有的DSP 平台上增加了浮点运算内核，在保持原有DSP 芯片的优点同时，能够执行复杂的浮点运算，可以大大节省代码的执行时间，具有精度高、成本低、功耗小、A/D 转换更精确快速等优点。

3.2.2 转子转速检测

矢量控制要求对转速进行闭环控制，电动机的转子位移、转速等信息检测的正确性和精度将直接影响调速系统的稳定性和控制精度，所以对转子转速的检测尤为重要。本文选用的是欧姆龙公司的E6B2－CWZ6C 型号的光电编码盘来检测转速。TMS320F28335 接收并记录来自光电编码盘发出的电平脉冲信号，输入的脉冲信号经DSP 内部处理计算，得出转子转速，转速nr的计算公式如下:

式中:m 为脉冲数;T 为时间。

3.2.3 定子电流检测

矢量控制系统中，因为有电流闭环，所以需要检测电动机定子电流，其检测精度同样对整个调速系统有很大影响。目前在电流检测方面采用霍尔传感器法的较多。用霍尔电流传感器检测电流较用电流互感器来检测，能够明显提高工作频带，具有线性好、响应快等优点。所以霍尔传感器法能够满足本系统的要求，本文采用霍尔传感器来检测定子电流。

3.2.4 输入功率检测

本文提出的节能搜索算法需要检测电动机运行时的输入功率，以作为搜索过程中判断的标准，当输入功率最低时即为电动机最优的节能运行状态。一般异步电动机驱动系统的输入功率可以由逆变器直流侧的两个直流量相乘得到:

但是考虑到逆变器的直流侧Ud和Id都含有不同成分的谐波，所以两个值相乘后的功率值不能直接用于节能搜索，要对其进行相应的滤波处理。但是滤波处理过程相对比较复杂，本文提出了一种替代的检测方法。系统的输入功率可以看作是电动机运行时候消耗的功率。对于三相异步电动机，其三相瞬时功率的和即为所消耗的功率:

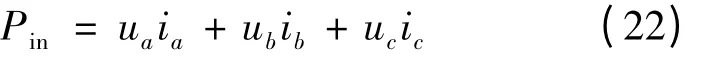
由于在矢量控制中的坐标变换，三相电压和电流转换成了两相解耦的直流量即usd，isd，usq，isq。又因为坐标变换是基于功率不变的原则，所以电动机的输入功率可以表示:

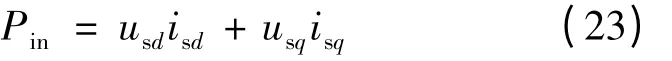
在实际系统中，usd，isd，usq，isq是程序的控制对象。可以很方便地获得，所以由式(23)计算出来的输入功率十分方便。

4 实验验证

本文实验验证了电动机在不同负载率下的节能控制过程。异步电动机参数:额定功率PN=2. 2 kW，额定转速n=1 430 r/min，极对数p =2，定子电阻Rs=0.865 Ω，转子电阻Rr=1.39 Ω，铁耗等效电阻RFe=98 Ω，定子电感Ls=0.159 78 H，转子电感Lr=0.159 78 H，互感Lm=0.156 H，转动惯量J =0.014 kg·m2。其结果如表1 所示。

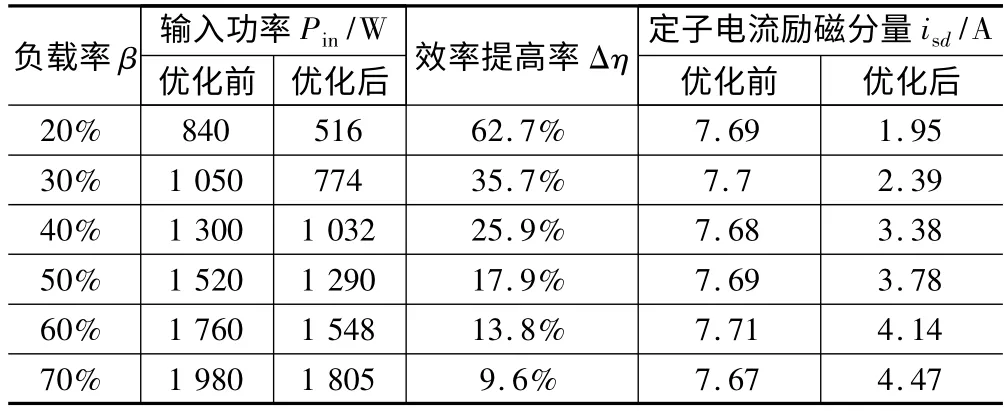
表1 节能控制数据

从以上数据看出，节能的效果还是非常明显的，尤其是在轻载时，效率提高率最高。

为了验证本文提出的控制策略，在一定程度上减少搜索过程中的转矩脉动，分别进行以下两组实验，给定的转子角速度为140 rad/s。结果如图4 和图5 所示。

图4 节能优化过程

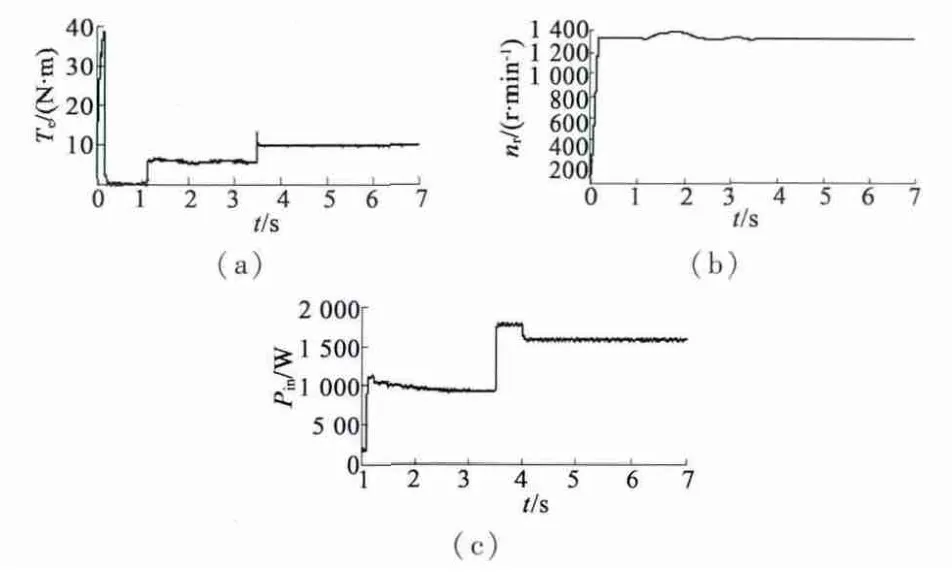
图5 节能优化过程(在线搜索定子电流最优比值)

图4 中，电机空载起动，1.1 s 时突加6 N·m 负载，待电机稳定后，在1.3 s 时启动搜索算法，搜索过程进行约2 s，输入功率从1100 W降到900 W;3.5 s 时电机突加10 N·m，磁链恢复额定值，延迟0.5 s 待电机稳定后，在4 s 时启动搜索算法，输入功率从1 760 W 降到1 580 W。从整个搜索过程可以看见，转矩有明显的脉动且电动机的转速也有一定程度的波动。

图5 的过程与图4 的过程大致一样，只是在4 s时没有启动搜索算法，而是将前一次搜索的结果(isq与isd的最优比值)直接用于此次节能优化。从图5(a)、图5(b)可以明显看出，在4 s 开始的搜索过程中，转矩和转速没有明显波动，整个搜索过程比较平稳，且最终节能效果相同。

5 结 语

通过对异步电动机损耗模型的优化分析得出，矢量控制中异步电动机稳态运行时，保持最低损耗的定子电流isq与isd比值不随电动机电磁转矩的变化而改变。本文提出以降低异步电动机运行损耗为目标，采用混合搜索法在线搜索最优比值。通过理论分析和实验结果表明，针对异步电动机轻载运行时存在的效率低下问题，本文提出的节能控制策略不仅能够降低矢量控制中异步电动机的运行损耗，提高效率，而且能够减少节能搜索过程中的转矩脉动，且不需要复杂的算法，易于实现。

［1］ 崔纳新，张承慧，杜春水. 变频调速异步电动机效率优化控制的研究进展［J］.电工技术学报，2004，19(5):36－41.

［2］ 高梅梅.异步电机矢量控制变频调速系统效率优化控制研究［D］.长沙:中南大学，2012.

［3］ 胡福年，胥露，刘亚军. 灰色预测理论在异步电动机调压节能中的应用［J］. 江苏师范大学学报，2013，31(1):42－43.

［4］ 李宗臣. 基于矢量控制的异步电机效率优化控制研究［D］.北京:北京交通大学，2010.

［5］ 徐飞，史黎明，李耀华. 异步电机在线参数观测及损耗控制策略［J］. 中国电机工程学报，2013，33(6):112－113.

［6］ BZAAI A M，KREIN P T. Review of method for real－time loss minimization in induction machines［J］. IEEE Transactions on Industry Application，2010，46(6):2319－2328.

［7］ KABOLI S，ZOLOGHADRI M R，ESMAEEL V K.A fast flux search controller for DTC－based induction motor drives［J］.IEEE Transactions on Industrial Electronics，2007，54(5):2407－2416.

［8］ CASADEI D，MENGONI M，SERRA G，et al. A control scheme with energy saving and DC－link overvoltage rejection forinduction motor drives of electric vehicles［J］. IEEE Transactions on Industry Application，2010，46(4):1436－1446.

［9］ 崔纳新，张承慧，孙丰涛.异步电动机的效率优化快速响应控制研究［J］. 中国电机工程学报，2005，25(11):118－123.

［10］ 张兴华，张振兴，王德明.电动汽车用感应电机直接转矩控制系统的效率最优控制［J］. 电工技术学报，2013，28(4):254－260.

［11］ 徐占国，邵诚.感应电机最大效率控制时损耗模型研究［J］.大连理工大学学报，2010，50(5):762－766.

［12］ 于伟光，祁新梅，郑寿森.基于定子磁链规划的异步电机最优效率控制［J］.电气传动，2012，42(1):14－15.

［13］ 马秀娟，刘金凤，李宏宇，等. 基于遗传算法的感应电机效率优化控制研究［J］. 微电机，2013，46(10):36－40.

［14］ 陈可，杨文焕.异步电机基于在线效率优化的模糊控制［J］.电机与控制应用，2010，37(12):38－41.

［15］ 李健健，刘新正.基于矢量控制的异步电动机节能运行的研究［J］.微电机，2010，43(3):14－17.

［16］ 李延峰，于海斌. 一种用于异步电机效率优化的混合搜索方法［J］.电机与控制学报，2009，13(3):337－341.

［17］ 任晋旗，李耀华，王珂.直线异步电动机的损耗模型与效率优化控制［J］.电工技术学报，2009，24(12):68－69.

［18］ FERNANDEZ－BERNAL F，GARCIA－CERRADA A，FAURE R.Model－based loss minimization for DC and AC vector－controlled motors including coresaturation［J］.IEEE Trans. on Ind.Appl.，2000，36(3):755－763.

［19］ 栾睿，彭珍瑞. 基于Matlab/Simulink 的异步电动机矢量控制系统仿真［J］. 电气应用，2011，(20):22.