中空环形行波超声波电动机赫兹接触模型

蒋春容，张津杨，董晓霄，张小莲

(1.南京工程学院，南京211167;2.东南大学，南京210096)

0 引 言

超声波电动机定子与动子之间的接触摩擦耦合是电机能量输出的关键，因此，建立定子与动子的接触模型，对超声波电动机的设计、优化乃至控制都具有重要作用。目前，国内外已有许多学者对超声波电动机接触模型进行研究。刘锦波等［1］采用解析法建立了环形行波超声波电动机摩擦传动模型，在该模型中，忽略了定转子接触界面上的粘滑分布，简化地认为接触界面上仅存在滑动分布情况。Storck等［2］采用解析法建立行波超声波电动机定转子粘弹性接触模型，指出摩擦材料的切向弹性变形既是定转子接触粘滞区形成的原因，也是影响摩擦损耗和电机效率的重要因素。曲建俊等［3］同样基于解析法建立了粘弹性接触模型，对摩擦材料粘结在定子表面上的接触模型进行了有益探索。考虑到接触的非线性，采用解析法建立超声波电动机的接触模型时，往往需要进行一定的简化，如忽略定子齿槽，将定子表面看成是连续的表面等。除了采用解析法，研究学者还提出了基于有限元法的超声波电动机接触模型。Maeno 等人［4－5］用有限元法研究了环形行波超声波电动机定转子的接触模型，计算了定子和转子接触表面质点的切向和法向的位移及速度，得到了电机的输出特性，同时指出接触区内存在复杂的粘滑分布。周盛强等［6］用ANSYS 软件的三维点点接触单元，对旋转行波超声波电动机定转子稳态接触问题建立了简化的有限元模型，分析电机稳定工作的某一时刻定转子的接触状态。Shen等［7］建立了行波超声波电动机简化的二维有限元接触模型，以分析接触界面内摩擦材料应力分布及劣化情况。采用有限元法建立接触模型时，可以考虑电机齿槽等复杂的结构，但需要较多的计算资源，当电机结构变化时，需要重新建立模型，因此比较费时。Ro Jong－Suk 等［8］总结比较了多种不同的行波超声波电动机接触模型，将不同接触模型的理论分析结果和实验结果进行对比，指出基于赫兹接触理论的模型具有最高的精度。

本文基于赫兹接触理论，建立一种无摩擦材料的中空环形行波超声波电动机的接触模型，分析定转子间的法向接触和切向力合成，进而得到电机的性能并进行实验验证。

1 电机的结构

所研究的中空环形行波超声波电动机的结构如图1 所示，此电机为佳能照相机镜头自动调焦系统所使用的超声波电动机［4］。电机的定转子均为金属弹性体圆环，无内部支撑结构，定转子通过一个波浪形圆环结构的弹簧紧压在一起。定子一面粘接沿厚度方向极化的压电陶瓷PZT，另一面开有齿槽，齿数为63。电机定子材料采用钢，转子材料为硬铝合金。电机定转子的截面如图2 所示，在定子和转子的接触表面上，均不粘接摩擦材料，转子通过较薄的法兰凸缘盘结构与定子齿接触，保证了预压力作用下转子的柔性变形。

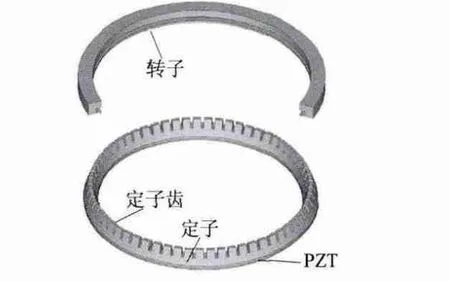
图1 中空环形超声波电动机的结构

图2 定转子截面

2 定转子接触分析

由于中空超声波电动机径向接触宽度比周向接触长度小得多，因此将三维接触问题简化为二维接触问题，并将定子表面看成是连续表面。定转子接触变形如图3 所示，图中，为静止坐标系，(x，z)为固定在定子行波波峰上的运动坐标系。在预压力的作用下，转子法兰凸缘盘产生柔性变形，使定转子在行波波峰附近接触，一个波长内定转子的周向接触长度为2L。

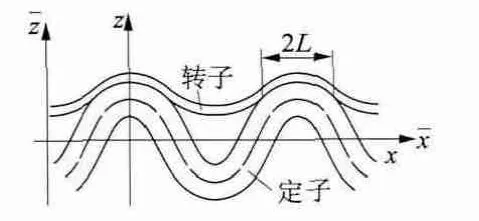
图3 定转子接触变形

2.1 定子运动方程

根据克希霍夫薄板理论，定子中性层的弯曲行波:

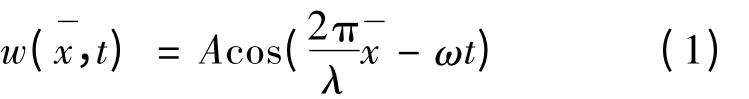
式中:A，λ 和ω 分别为定子中性层弯曲振动的振幅、波长和角频率。运动坐标系(x，z)和静止坐标系)之间有如下关系:

将式(2)代入式(1)可得在(x，z)坐标系下的行波运动:

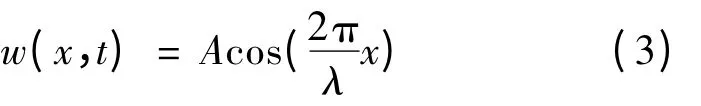
定子表面质点的切向速度vs(x):

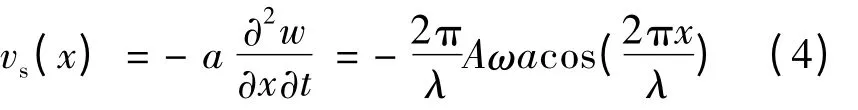
式中:a 为定子中性面到定子齿面的距离。

2.2 法向接触分析

假设转子法兰凸缘盘完全弹性，定子在行波波峰附近等效为一个等曲率半径的圆柱体，其曲率半径ρk满足:

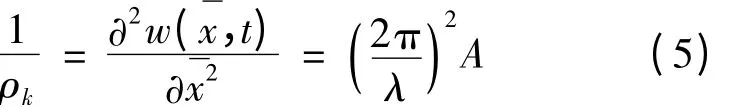
等效圆柱体的直径D:

设定转子间施加的法向预压力为FN，则每个波长内单位长度的平均法向力Funit:

式中:n 为定子行波的波峰数，b 为定转子径向接触宽度。根据赫兹接触理论［9］，一个波长内定转子间的周向接触长度:

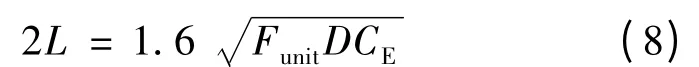
CE由下式计算得到:

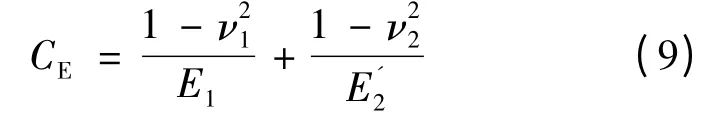
式中:ν1和E1分别为定子的泊松比和弹性模量;ν2和分别为转子的泊松比和等效弹性模量。考虑到转子法兰凸缘盘的柔性变形，转子的等效弹性模量取为转子实际弹性模量E2的10%。由式(8)可求得一个波长内周向接触半长度L 的大小。在接触区域［－L，L］范围内，赫兹接触压力分布满足:

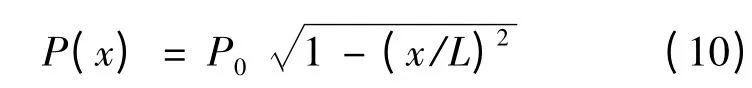
式中:P0为接触压力的幅值。稳态时，由转子法向受力平衡可得:

将式(10)代入式(11)，求解可得P0:

2.3 切向推力合成

定子上的行波运动通过接触摩擦传递给转子，形成转子的旋转运动。假设定转子间的滑动摩擦系数为μd，在接触区域内法向接触压力作用下，合成的转子上的切向推力FT:

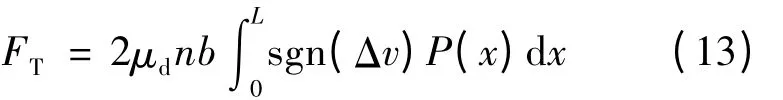
式中:符号函数sgn(Δv)定义:

Δv 为接触区内定子表面质点的切向速度vs(x)与转子转速vr的大小之差:

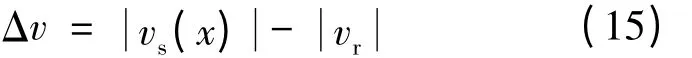
在接触区域［0，L］范围内，设x =x0处，Δv =0，则式(13)可化:

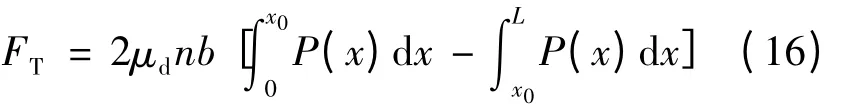
需要注意的是，在由Δv =0 求得x0时，若x0＞L，则说明整个接触区均为推力，式(16)计算时应取x0=L。将式(10)代入式(16)求解可得:

式中:θ0=arcsin(x0/L)。转子的输出转矩T:

式中，r 为定转子等效接触半径。

3 仿真结果与验证

中空环形行波超声波电动机的参数如表1 所示。

表1 中空超声波电动机的参数

定转子周向接触长度取决于预压力的大小。当定子振幅保持1 μm 不变时，不同的预压力下，一个波长内周向接触半长度L 与预压力FN的关系如图4 所示。随着预压力增大，L 先迅速增加，而后增加速度趋缓。在相同振幅、不同的预压力下，电机的输出转矩T 与转速n 之间的变化关系如图5 所示。随着预压力增大，堵转转矩增大，空载转速减小。

当保持预压力为15 N 不变，定子振幅变化时，电机的空载转速n0和堵转转矩Tst随振幅变化的趋势，如图6 所示。随着振幅增大，空载转速n0线性增大，堵转转矩先增大，而后维持在最大值不变。

图4 L 与FN 的变化关系

图5 不同预压力下电机的T－n 特性曲线

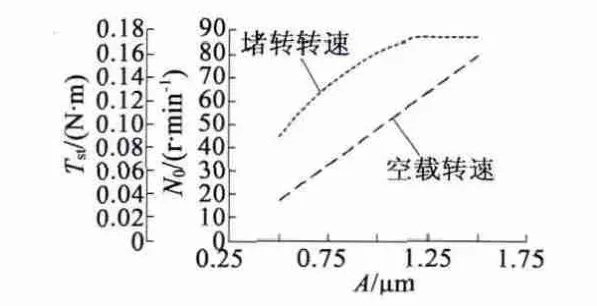
图6 电机空载转速和堵转转矩与定子振幅的关系

电机正常工作时所施加的预压力为15 N，定子振幅为1 μm，此时，定转子间的法向接触压力分布如图7 所示。接触压力分布为关于定子行波波峰对称的半椭圆形状。将计算得到正常工作状态下电机的转矩－转速(T－n)特性与实验测试数据进行比较，如图8 所示，其中实验测试数据来自于文献［5］。由图8 可知，理论计算值与实验测试值基本吻合，验证了所提出的赫兹接触模型的有效性。

图7 接触区内接触压力分布

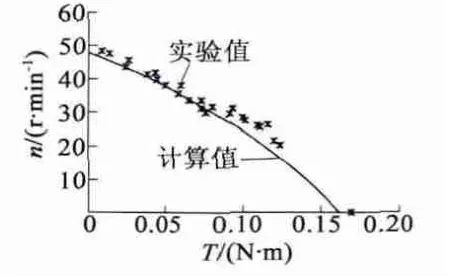
图8 T－n 特性曲线的计算值与测量值对比

4 结 语

1)随着预压力的增大，定转子间的周向接触长度先迅速增加，而后增加速度趋缓。

2)定子振幅相同的情况下，随着预压力的增大，堵转转矩增大，空载转速减小。

3)保持预压力不变，定子振幅增大时，电机空载转速随着振幅增大而线性增加，堵转转矩先增大，而后维持在最大值不变。

4)定转子间的接触压力分布为关于定子行波波峰对称的半椭圆形状。

5)电机的转矩－转速特性计算值与测试值基本吻合，验证了所提出的模型的有效性。

［1］ 刘锦波，陈永校. 超声波电机定转子接触的摩擦传动模型及其实验研究［J］. 中国电机工程学报，2000，20(4):59－63.

［2］ STORCK H，WALLASCHEK J.The effect of tangential elasticity of the contact layer between stator and rotor in travelling wave ultrasonic motors［J］. International Journal of Non－Linear Mechanics，2003，38(2):143－159.

［3］ QU Jianjun，SUN Fengyan，ZHAO Chunsheng.Performance evaluation of traveling wave ultrasonic motor based on a model with visco－elastic friction layer on stator［J］. Ultrasonics，2006，45(1－4):22－31.

［4］ MAENO T，TSUKIMOTO T，MIYAKE A.Finite－element analysis of the rotor/stator contact in a ring－type ultrasonic motor［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，1992，39(6):668－674.

［5］ MAENO T，BOGY D B.FE analysis and LDA measurement of the dynamic rotor/stator contact in a ring－type ultrasonic motor［J］.Journal of Tribology，1993，115(4):625－631.

［6］ 周盛强，赵淳生，黄卫清. 旋转型行波超声电机接触界面的空间域分析［J］. 中国电机工程学报，2010，30(12):63－68.

［7］ SHEN Shengnan，LEE H P，LIM S P，et al. Contact mechanics of traveling wave ultrasonic motors［J］. IEEE Transactions on Magnetics，2013，49(6):2634－2637.

［8］ RO J－S，JUNG S－Y，LEE C－G，et al.Survey of a contact model and characteristic analysis method for a travelling wave ultrasonic motor［J］. International Journal of Applied Electromagnetics and Mechanics，2014，46(3):437－453.

［9］ JOHNSON K L. Contact Mechanics［M］. Cambridge:Cambridge University，1985:84－106.