一种改进的经验模态分解算法与测井信号去噪
2015-01-13高丙坤崔行悦孙灵川
高丙坤 崔行悦 张 莉 孙灵川
(1.东北石油大学电气信息工程学院,黑龙江 大庆163318;2.北京邮电大学信息与通信工程学院,北京 100876)
经验模态(EMD)分解信号处理方法不需要先验信息,能够依据信号的自身特性,自适应地提取信号的固有模态函数,能够把信号进行平稳化处理,适用于非线性、非平稳性信号。该方法打破了常规的以线性和平稳性为基础的傅里叶变换及小波变换等传统时频域分析方法,开辟了信号处理与分析的新途径。由于经验模态分解过程存在端点效应,导致虚假分量的产生和边界信号的失真,为此笔者对端点效应进行了抑制,并将改进后的经验模态分解算法应用于核磁共振油气井探测回波信号处理中,有效地滤除了噪声信号。
构造原始信号x(t)为:
x(t)=2sin(20πt)+50sin(50πt)
(1)
对信号进行EMD分解后,得出各固有模态分量(imf)和残余分量(res)如图1所示。
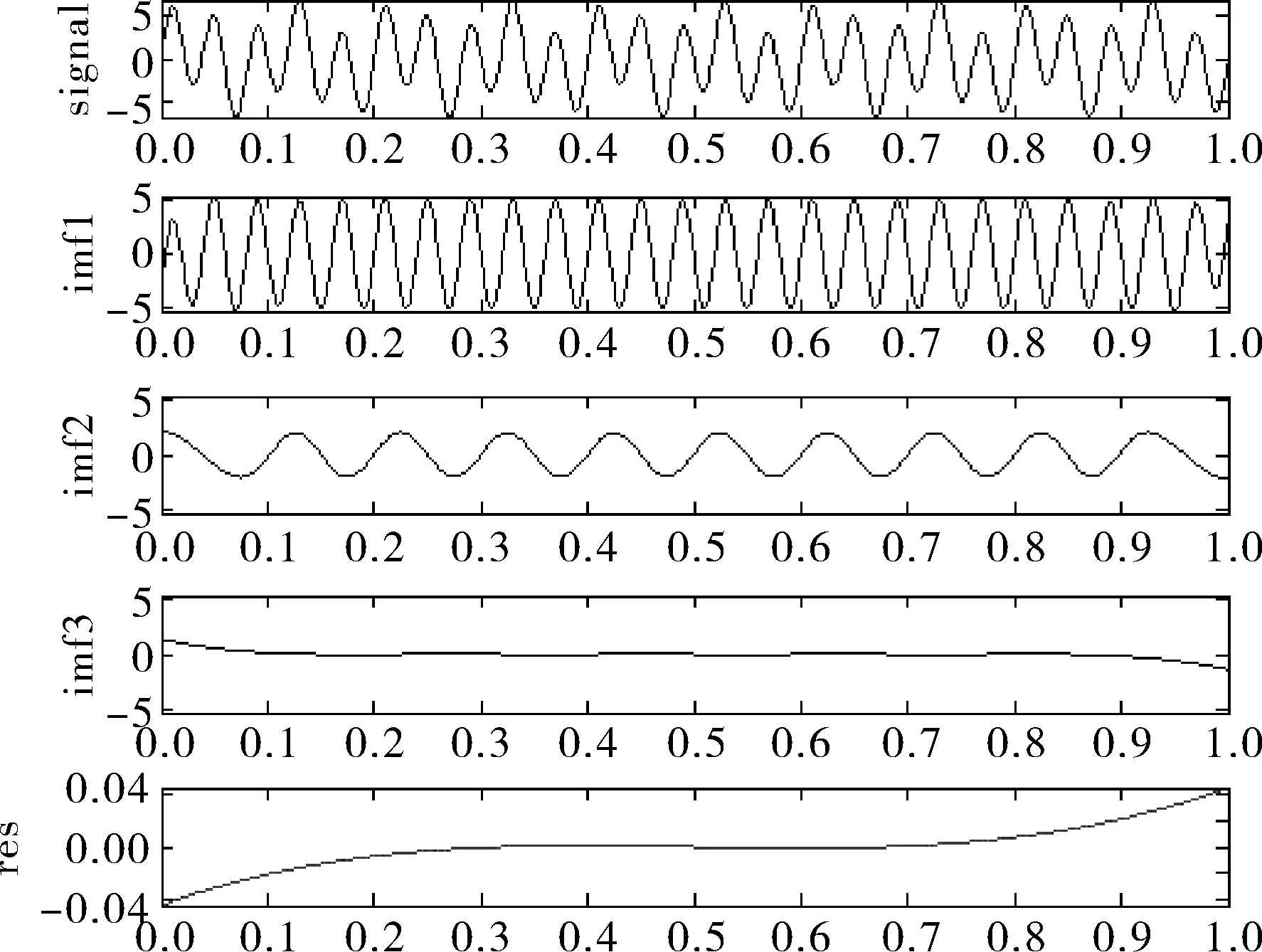
图1 信号EMD分解
从图1可以看出,第一个imf分量包含了原始信号x(t)的25Hz正弦信号,第二个imf分量包含了原始信号x(t)的10Hz的正弦信号,但在实际分解后出现了不应该存在的第三个imf分量,即原始信号经过EMD分解后产生了虚假分量。此外,第一个imf分量边界附近出现了严重失真,从而导致在第二个imf分量的边界也产生了这种失真,即第一个imf分量端点处的失真污染了后面分解出的固有模态函数,这种现象称之为端点效应。
端点效应是由于EMD分解过程中采用了三次样条插值函数进行上下包络的拟合造成的。由于在运用三次样条函数的过程中,不能确保原始信号的两端点就是信号的极值点,在端点附近没有能约束极值点的信息,导致拟合出的包络线与原始信号的实际包络线偏离。在原始信号的高频分量中,由于其极值点距离较近,端点效应仅仅局限在信号端点附近很小的范围内,因此影响较小;但是在低频分量中,由于信号的极值点间距较大,导致端点效应很容易影响到信号的内部。
2 EMD分解后的Hilbert变换
为了根据瞬时频率的定义计算出瞬时频率,从而进行时频域分析,需要对分解出的每一个imf分量进行Hilbert变换。由于分解出的残余分量res为单调函数或者常数,故在做Hilbert变换时舍去残余分量,则原始信号为:
(2)
因此,对于任意的imf分量ck(t),其Hilbert变换为:
(3)
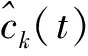
其中,信号的幅值信息为:
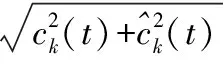
信号的相位信息为:
故:
ck(t)=Re(ak(t)ejφk(t))
由于瞬时频率为:
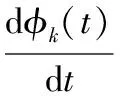
对上式两边取积分,得:
因此,原始信号可以表示为:

(4)
这就是Hilbert谱形式。对式(1)做HHT谱分析,其结果如图2所示,可以看到两条近似平行的直线,代表着频率的聚集程度,同时也可以清楚地看到端点效应引起的边缘失真。

图2 Hilbert谱分析
3 EMD分解端点效应的改进
端点效应的总体原因是在原始信号进行三次样条采样时缺少了一个能够约束端点处的条件,即没有使用某种条件去判断端点是否是极值点。为了消除这种端点问题带来的EMD分解失真问题,出现了基于神经网络的数据延拓法[1]、镜像闭合延拓法[2]及基于AR模型的时间序列线性预测方法[3]等,这些方法通过补充数据来抑制端点效应。采用适应延长边界特征点的办法对包络线进行拟合,然后再截取有效长度能够抑制端点效应,但会增加计算量。为此,在边界局部特征延拓法[4]的基础上,通过判断原始信号的端点能否作为极值点插入到新的上下包络中,来抑制端点效应。实施步骤为:
a. 求出信号所有的极值点。
b. 设信号的采样长度为Δt,该信号有M个极大值和N个极小值,则极大值对应的时间序列为Tmax(1),Tmax(2),…,Tmax(M),每一个时间点对应的函数值为Xmax(1),Xmax(2),…,Xmax(M);极小值对应的时间序列为Tmin(1),Tmin(2),…,Tmin(N),每一个时间点对应的函数值为Xmin(1),Xmin(2),…,Xmin(N),则新的端点处的极值点平均幅值为Xmax=(Xmax(1)+Xmax(2)+Xmax(3)+Xmax(4))/4和Xmin=(Xmin(1)+Xmin(2)+Xmin(3)+Xmin(4))/4,平均时间间隔为Tmax=(Tmax(5)-Tmax(1))/4和Tmin=(Tmin(5)-Tmin(1))/4。
c. 计算出平均幅值和平均时间间隔后,放入原信号端点的两侧。
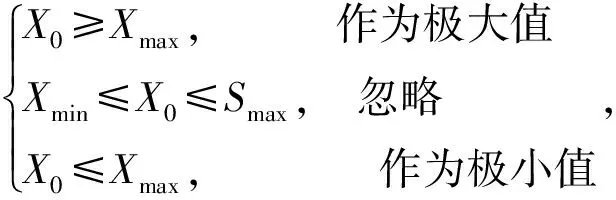
e. 对添加后的信号进行拟合,得出原始信号的上下包络线。
对式(1)经过端点处理后的信号Hilbert时频谱如图3所示,端点效应得到了有效抑制,体现了更好的时频聚集性,更加准确地描述了信号频率在时间轴上的变化特征。
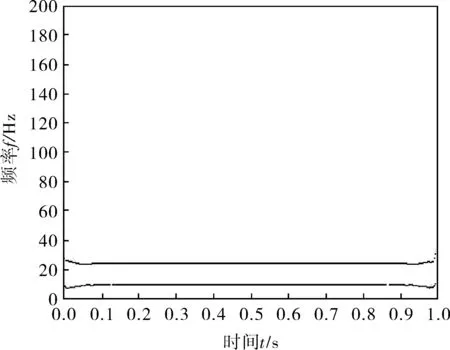
图3 经过端点处理的Hilbert谱
4 改进端点效应的EMD方法在测井信号去噪中的应用
利用核磁共振技术对油气探井测试时得到的回波信号含有大量噪声,其Hilbert谱如图4所示,导致所测得的原始信号不能准确反映井下油气信息特征。采用改进的EMD分解去噪后Hilbert谱如图5所示,保留下来的是低频中的有用信号和少量的噪声,为油气勘探和开发提供了有效数据。
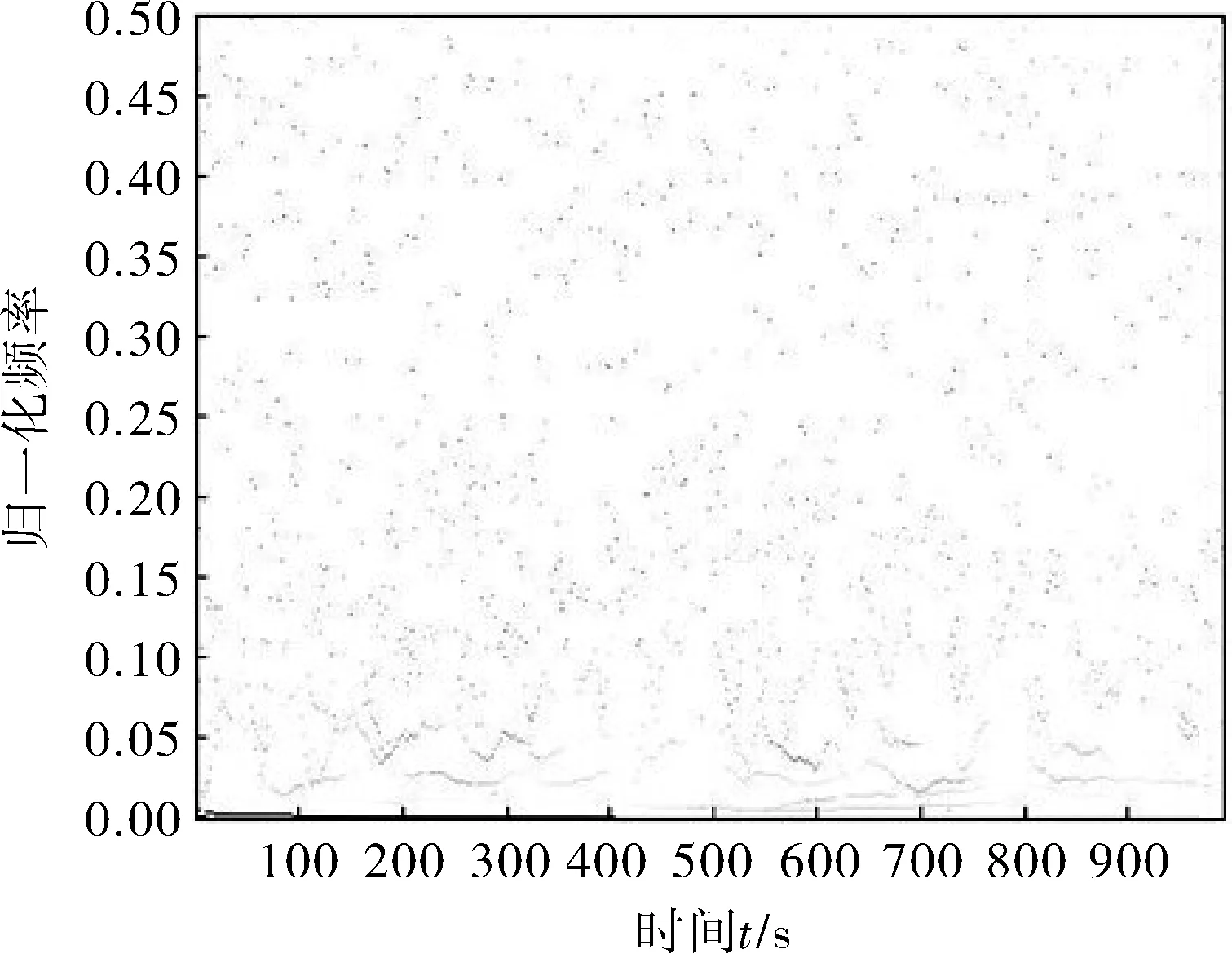
图4 测井回波信号Hilbert谱

图5 测井信号经改进的EMD处理后的Hilbert谱
5 结束语
基于边界局部特征延拓法,通过判断原始信号的端点能否作为极值点插入到新的上下包络中,有效抑制了EMD分解方法中的端点效应。将改进的EMD分解算法应用于核磁共振油气井探测回波信号处理中,通过Hilbert谱分析可知,高频噪声被有效滤除。
[1] 邓拥军,王伟,钱成春,等.EMD方法及Hilbert变换中边界问题的处理[J].科学通报,2001,46(3):257~263.
[2] 黄大吉,赵进平,苏纪兰.希尔伯特-黄变换的端点延拓[J].海洋学报(中文版),2003,25(1):1~11.
[3] 张郁山,梁建文,胡聿贤.应用自回归模型处理EMD方法中的边界问题[J].自然科学进展,2003,13(10):48~53.
[4] 林丽,周霆,余轮.EMD算法中边界效应处理技术[J].计算机工程,2009,35(23):265~268.
