基于多水质参数融合的锅炉连排复合控制
2015-01-13周晓东张腾宇赵鑫岩王冰礁曹生现
王 恭 周晓东 张腾宇 赵鑫岩 王冰礁 曹生现
(1.东北电力大学自动化工程学院,吉林 吉林 132012;2.山西新华化工有限责任公司,太原 030008; 3.华能罗源发电有限责任公司,福州 350026)
随着火电机组容量的不断增大,对锅炉连续排污的控制要求也进一步提高。目前,锅炉连排普遍采用以炉水电导率为被控量的PID反馈控制系统。随着电厂控制技术的发展,锅炉连排控制技术不断改进,文献[1,2]指出小容量锅炉在工业生产的连排过程中,以排污率为标准,根据蒸汽量计算得到连排流量,对其进行有效控制,可取得较好的排污效果。文献[3]基于锅炉连排流量由多水质参数共同影响的特点,应用现场实验数据,建立了炉水电导率和二氧化硅浓度与连排流量的函数关系。综合比较这些控制策略在炉水连排中的控制效果,笔者根据炉水连排控制的实际情况和过程特点,建立了一种能够应对连排过程中大迟延、多变量和强时变性的多水质参数连排复合控制系统,并进行了仿真验证。
1.1 复合控制系统策略的确定
锅炉连排控制存在多变量及大迟延等特点,而前馈-反馈控制策略在克服迟延和扰动方面具有一定的优势[4,5],为确保炉水pH值、电导率、磷酸根离子和二氧化硅4个水质参数指标适应锅炉运行的要求,设计了锅炉连排复合控制系统,系统结构如图1所示。其中被控量为炉水电导率,执行器为连排流量阀,输出为连排流量的调整值。在该控制系统设计中,前馈控制器采用数据融合算法[6~10],实现多水质参数与连排流量的关联,融合结果作为前馈控制量,而在反馈环节中采用了模糊自整定PID控制方式,既具备了模糊控制的鲁棒性又兼顾了PID控制高精度的特点[11],可根据排出炉水电导率实时值对PID的控制参数进行连续调整,以适应参数时变的控制过程。

图1 锅炉连排复合控制系统结构框图
1.2 控制系统参数辨识
考虑到连排流量和炉水电导率之间的关系在电厂生产中难以确定,因此,笔者基于电厂锅炉排污实际运行情况,设计了控制系统参数模拟实验平台,具体结构如图2所示。实验系统模拟了恒压环境下影响炉水含盐量的补给水、锅炉连排及蒸发等环节的锅炉水循环过程,然后根据实验数据对系统被控对象进行参数辨识。实验得到的阶跃响应曲线如图3所示,由曲线分析可知该系统具有明显二阶过阻尼特性,且为自平衡系统,参考文献[12]系统辨识的算法,利用被控对象阶跃响应多组实验数据,辨识对象的传递函数,确定的系统传递函数如下:

(1)

图2 模拟锅炉连排系统结构
1.3 前馈控制器的设计
前馈控制器的设计采用数据融合算法,两级融合模型采用局部并行总体串行的复合结构,然后通过BP神经网络融合算法,预测锅炉连排流量,并以此克服水质参数扰动对系统带来的影响。


(2)
二级融合。二级融合采用BP神经网络算法,建立各水质参数与连排流量的关联,根据各水质参数数据实时、准确地完成锅炉连排流量的预测。
设xk表示第k次迭代的权值和阈值所组成的向量,新的权值和阈值组成的向量xk+1可根据下式求得:
xk+1=xk+Δx
(3)
对于牛顿法,则有下式:
Δx=-′2E(x)J-1·′E(x)
(4)
式中 ′E(x)——梯度;
′2E(x)——误差指标函数E(x)的Hessian矩阵。
确定误差目标函数后,由Jacobian矩阵推导出的L-M表达式如下:
Δx=[JT(x)J(x)+μI]-1J(x)e(x)
(5)
式中I——单位矩阵;
μ——常数,μ>0。
μ作为调整因子用于控制L-M算法的迭代,通过自适应调整该值,L-M算法可以使梯度下降法与高斯牛顿法较好的结合。
二级融合的输入为一级融合后的数据,输出为连排流量。BP神经网络采取单隐含层、四输入、一输出的三层网络结构。将隐含层神经元个数设为7,相邻层的传递函数依次选取“tansig”、“purelin”函数。训练函数选取“trainlm”。设定的网络参数为:学习速率0.05,动量因子0.9,训练目标最小误差0.001。
为实现连排流量的准确预测,二级融合网络选用某火电厂600MW亚临界机组110组样本数据(表1),对网络进行训练和验证。
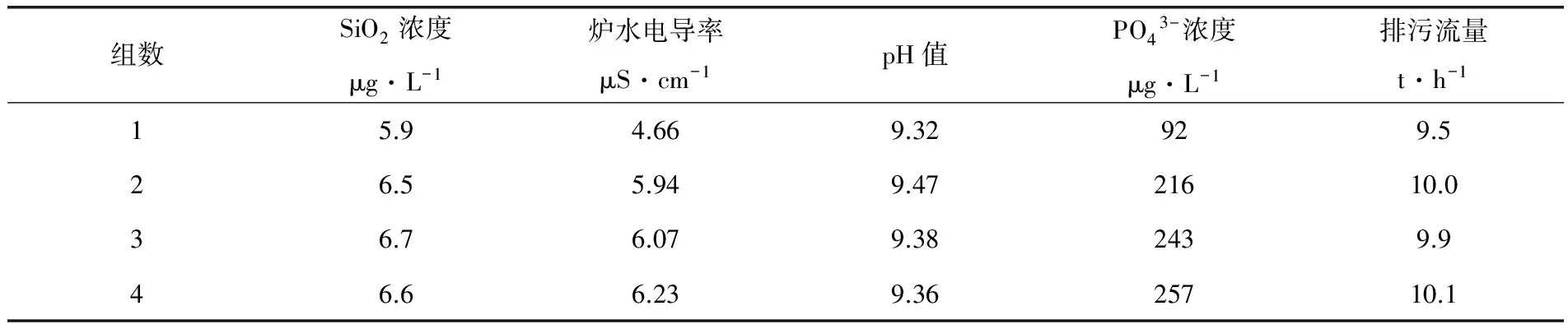
表1 样本数据

(续表1)
1.4 反馈控制器设计
反馈控制器采用模糊自整定PID控制算法,实现对PID参数KP、KI、KD的在线调整。模糊控制器有两个输入,分别为设定的炉水电导率和出水电导率的偏差E和偏差变化率Ec,取其对应的基本论域为[-6,6]和[-5,5],量化因子为5和2。输出量为PID控制器的增量ΔKP、ΔKI、ΔKD,取其对应的基本论域为[-0.6,0.6]、[-0.012,0.012]和[-1.2,1.2],比例因子为0.2、0.04和0.40。为提高系统的灵敏度,模糊子集选取{NB,NM,NS,ZO,PS,PM,PB}。为了便于算法实现,隶属函数选取隶属度幅值等于模糊论域步长的三角形隶属度函数,建立模糊控制规则(表2),利用重心法求解模糊控制量。

表2 三参数模糊控制规则表
通过上述步骤,计算模糊控制器的3个输出值ΔKP、ΔKI、ΔKD,利用临界比例带法确定的式(1)所示控制对象的初始控制参数为KP=1.2,KI=0.031,KD=11.27。至此模糊自整定PID控制器的参数实时调整如下:
(6)
2 控制系统仿真分析
在一级融合过程中选取某火电厂600MW亚临界机组炉水中磷酸根离子某一段时间的测量值进行处理,处理结果如图4所示。由数据曲线可以看出,融合后数据曲线较为平滑,原始数据均方差为0.37,而融合后数据均方差为0.11。由此说明经数据融合算法处理的数据可提高测量数据的准确度。
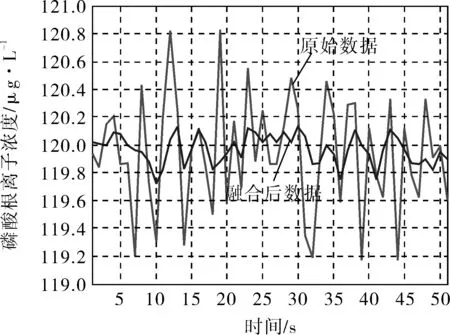
图4 一级融合数值与原始数值对比
二级融合处理结果如图5所示,图中实际值和预测值能基本吻合,只有少数预测值与实际值有所差别,经计算其平均绝对误差为3.78%。因此设计的二级融合网络能够较为准确地实现连排流量的预测。

图5 二级融合数值与实际值对比
选取30组测试数据分别采用两级融合和BP神经网络进行排污流量预测,计算结果如图6所示,两级融合算法平均误差为2.92%,BP神经网络平均误差为5.76%。由此说明设计的两级数据融合算法在满足系统实时性的要求下,预测值更为准确。
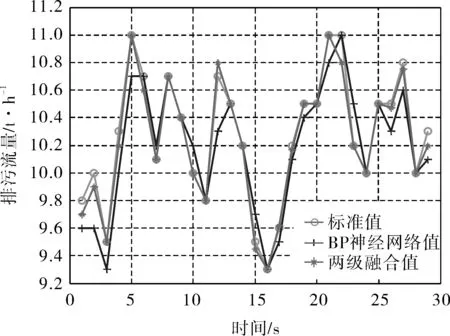
图6 两级融合与BP神经网络预测值对比
鉴于炉水加药对连排流量影响较大,特别是炉水加磷对炉水电导率影响最为显著,为此选取磷酸根浓度作为干扰量。采用了典型的一阶惯性模型,比例系数设为1.5,惯性时间常数T设为20,基于Simulink分别对前馈-反馈控制器、传统PID控制和笔者设计的复合控制进行仿真,仿真曲线如图7所示。
仿真结果表明:前馈-反馈控制器相比传统PID控制,超调量由34.0%下降到19.6%,调整时间由传统PID的237s缩短到185s,且系统振荡周期明显缩短;当加入干扰量时,系统的炉水电导率波动较小,且能快速消除扰动带来的影响。引入模糊自整定PID控制器后,系统超调量控制到10.5%,调整时间相比前馈-反馈控制缩短了27s,外界扰动的影响趋于平稳,表明建立的复合控制模型能更好地适应实际工况,与传统控制系统对比,具有控制精度高、反应速度快、抗干扰能力强及动态性能稳定等特点。
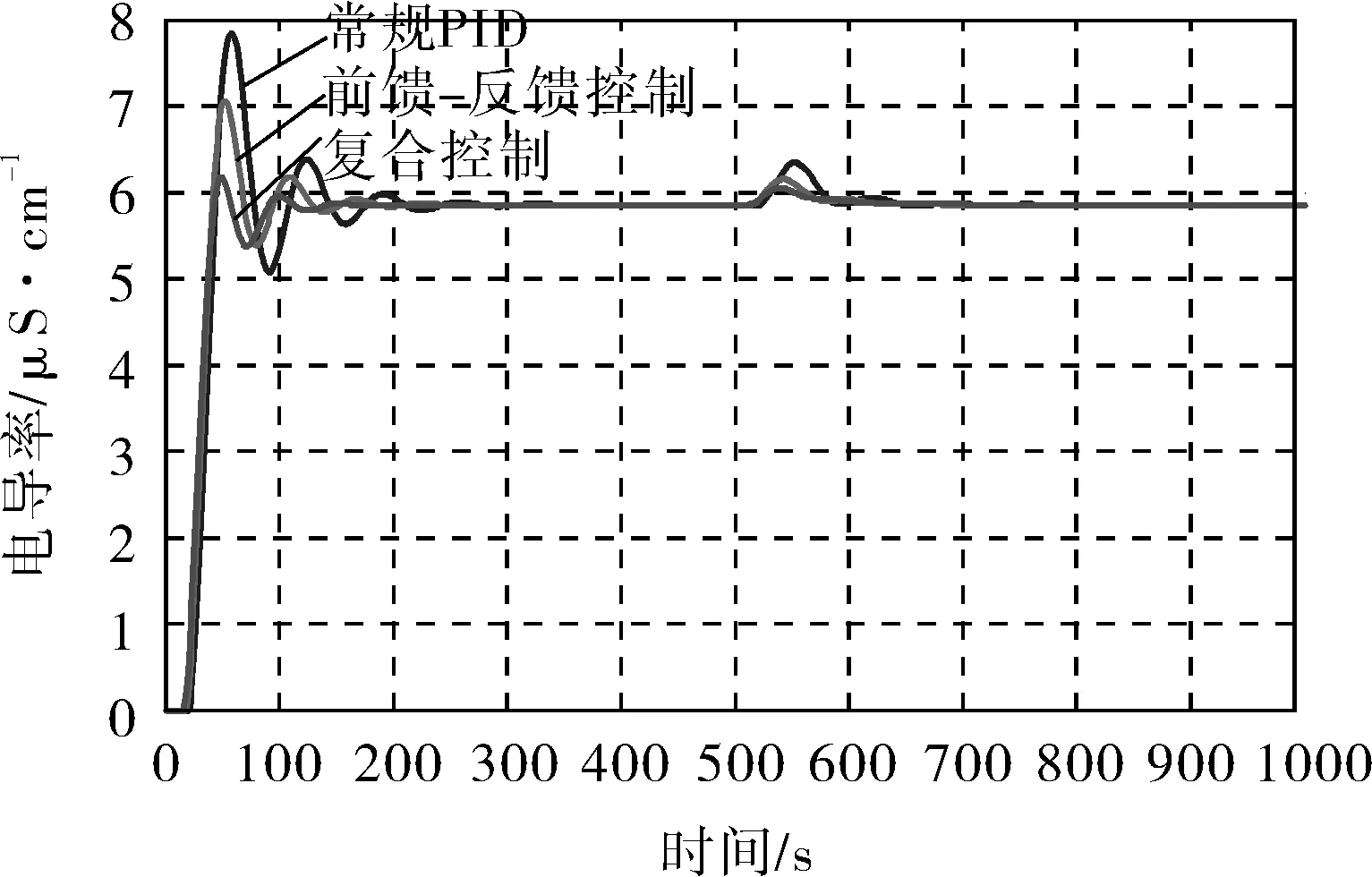
图7 复合控制系统仿真对比曲线
3 结束语
针对锅炉连续排污过程的特点,利用数据融合算法建立了预测排污流量的前馈模型,结合模糊PID控制器作为反馈校正,设计了锅炉连排复合控制系统,实现了对连排流量的实时调整和炉水电导率的有效控制。控制系统仿真结果表明:该系统具有较好的动、静态性能,当引入较大的外部扰动时,系统表现出较好的鲁棒性。
[1] 徐庆新.完善锅炉连续排污控制与节能增效[J].工业锅炉,2007,(2):48~51.
[2] Li M,Zhang H B,Zhang W,et al.Optimal Energy-saving Control of the Steam Boiler Blowdown[J].Industrial Instrumentation & Automation,2011,(6):77~79.
[3] 郭鹏.模糊前馈与模糊PID结合的风力发电机组变桨距控制[J].中国电机工程学报,2010,30(8):123~128.
[4] 韩广,乔俊飞,薄迎春.溶解氧浓度的前馈神经网络建模控制方法[J].控制理论与应用,2013,30(5):585~591.
[5] 王德明,王莉,张广明.基于遗传BP神经网络的短期风速预测模型[J].浙江大学学报(工学版),2012,46(5):837~841,904.
[6] 郭鹏程,罗兴锜,王勇劲,等.基于粒子群算法与改进BP神经网络的水电机组轴心轨迹识别[J].中国电机工程学报,2011,31(8):93~97.
[7] 邵良衫,付贵祥.基于数据融合理论的煤矿瓦斯动态预测技术[J].煤炭学报,2008,33(5):551~555.
[8] 王恒,贾民平,陈左亮.基于多传感器信息融合技术的球磨机料位测控系统[J].电力自动化设备,2012,32(9):138~141.
[9] 张雪,丁艳军,郑康捷,等.基于多信息融合的旋流燃烧器燃烧状态评价[J].中国电机工程学报,2010,30(2):23~28.
[10] 顾丹珍,艾芊,陈陈,等.自适应神经网络在负荷动态建模中的应用[J].中国电机工程学报,2007,27(16):31~36.
[11] 王华强,石亚娟,王健波.神经网络模糊PID在水轮机调速系统中的应用[J].合肥工业大学学报(自然科学版),2012,35(9):1187~1191.
[12] 宋志安,王文馨.由阶跃响应曲线辨识传递函数的图解方法[J].山东科技大学学报(自然科学版),2003,22(1):61~63.
