基于相关性小波奇异熵的滚动轴承故障特征提取

刘 霞 孙美岩 薛海峰 庞永贵

(1.东北石油大学电气信息工程学院，黑龙江 大庆 163318；2.中国石油集团测井有限公司，西安 710021； 3.大庆物探一公司，黑龙江 大庆 163357)

根据传感器测得的振动信号对机械故障进行诊断，是机械故障诊断中一种常用的有效方法。其中的核心技术是通过分析、处理振动信号用以提取机械故障信号的特征。常用的故障特征提取方法是短时傅里叶变换及Wigner-Ville分布等。短时傅里叶变换是应用最基本的时频分析方法，同时也是一种时窗大小和形状都固定不变的分析方法。Wigner-Ville分布有很多优点，如对称性及重构性等，但也存在交叉干扰项的问题，此问题构成了时频特征模糊不清的现象，同时也受噪声的影响。为了解决以上问题并更有效地提取故障信号的特征，笔者提出了相关性小波奇异熵的算法，将小波变换、相关性、奇异值分解和信息熵理论有效地结合在一起。首先，由于轴承振动信号具有非线性、非平稳的性质[1]，而小波分析被称为信号的显微镜，适合分析非平稳信号；其次，由于信号的小波变换在各尺度间具有较强的相关性，而噪声的小波变换在各尺度却没有明显的相关性，因此引入相关计算，以去除噪声对有效信号的影响；当轴承出现不同的故障时，故障信号的奇异值也会发生相应的变化，再对相关计算后的系数进行奇异值分解；最后，利用信息熵进行计算，信息熵是对不规则复杂程度的度量。以熵值作为故障特征向量输入到概率神经网络里进行故障识别。

1.1 小波变换

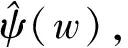
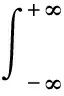
(1)

则称ψ(t)为一个小波函数或母小波。将母小波ψ(t)经过伸缩和平移后生成：

(2)

称其为一个小波序列。其中，a为尺度因子，b为平移因子。

(3)

相应的离散小波函数为：

(4)

设有离散采样序列x(n),n=1,2，…，N，如果以x(n)表示在尺度j=0时刻的近似值，a0=x(n)，则x(n)小波变换由下式确定：

(5)

其中，H和G分别为高通滤波器和低通滤波器，aj和bj分别为信号尺度的近似系数和细节系数。故障振动信号x(n)经过尺度1,2,…,j层分解，最终分解为d1,d2,…,dj,aj，它们包含了信号从高频到低频不同频带的信息。

1.2 相关性理论

根据信号与噪声的小波变换在各个尺度下不同的传播特性，引入相关计算，以去除噪声对信号的影响。介绍一下相关系数，其定义为：

Cor(j,k)=Wf(j,k)·Wf(j+1,k)

(6)

Wf(j,k)={aj(k),dj(k)}

(7)

式中Cor(j,k)——分解尺度j上k点的相关系数；

Wf(j,k)——尺度j上k点的小波系数。

对相关系数进行规范化处理以便使小波系数和相关系数能够具有对比性。

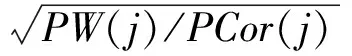
1.3 奇异值分解原理

当轴承出现不同的故障时，振动信号中的频率分布会发生变化，信号的奇异值也会发生相应的变化[3～5]。同时，矩阵奇异值还具有比例不变性和旋转不变性。为了检验轴承故障的类型，在小波分解的基础上，计算各个尺度上奇异值的改变。首先对规范化以后的相关系数进行相空间重构。

设j层上相关计算后的信号为Dj={dj(k)}。将Dj中dj(1),dj(2),…,dj(n)作为相空间的第一个矢量，然后右移1步即可得到第二个矢量，依次类推，可以构造出一个(N-n+1)×n维矩阵A，一般说来，A多采用Hankel矩阵形式：

(8)

对相空间重构的信号A进行奇异值分解。设A是m×n维的正交矩阵，SVD可以把矩阵A分解成3部分：

A=UΛVT

(9)

其中，U是m×m维的正交矩阵，V是n×n维的正交矩阵，Λ=diag(α1,α2,…,αN)为对角矩阵，r为矩阵A的秩。U和V矩阵分别称为左奇异矩阵和右奇异矩阵，α1，α2，…，αN为矩阵A的奇异值，且呈递减顺序，即α1≥α2≥…≥αN≥0，并且每个奇异值的重要性是不同的。

1.4 相关性小波奇异熵

信息熵是信源输出信息不确定性的定量评价指标，也是表征信源总体特征的一个量。信息熵对于调制信号的内在信息具有很好的刻画能力，应用比较广泛。因此可以将信息熵应用于对轴承故障信号的特征提取[6]。

(10)

其中，pi=αi/α，α为所有奇异值之和，即α=α1+α2+…+αN。

1.5 相关性小波奇异熵特征提取算法

相关性小波奇异熵特征提取算法的步骤如下：

a. 对轴承故障信号进行小波分解；

b. 根据相关公式对各尺度小波分解系数进行计算和规范化处理；

c. 利用式(8)对每层相关计算后的系数进行相空间重构；

d. 对每层相空间重构的矩阵A进行奇异值分解；

e. 根据式(10)计算故障信号的相对性小波奇异熵；

f. 将熵值作为特征向量对滚动轴承进行特征提取。

2 改进算法的性能分析

2.1 容噪能力分析

当滚动轴承出现不同故障时,振动信号会出现调制现象,具体现象为在共振频率周围存在边频带,边带间隔就是调制频率,也是轴承故障特征频率。为此，建立滚动轴承仿真信号为：

x(k)=e-at×sin2fckT

(11)

(12)

式中fc——载波频率；

fm——调制频率；

T——采样时间；

α——指数频率。

当α=800，fm=100Hz，fc=5000Hz，T=1/25000s，信号长度为8 192点时，信噪比为3dB，原信号和加噪信号如图1所示。选择db5小波对其进行十二层小波分解，对原信号和加噪信号计算相关性小波奇异熵，其中第十一层和第十二层的熵值相等，具体数据见表1。

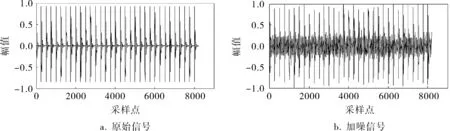
图1 原始信号和加噪信号波形

信号第一层第二层第三层第四层第五层第六层第七层第八层第九层第十层第十一/十二层原始信号4．35144．43874．21573．79383．04452．39241．68871．28601．08720．72750．4055加噪信号4．31584．44514．21823．77632．97922．36161．69641．27701．07650．76300．4171

通过仿真研究可以看出，加噪前后的相关性小波奇异熵没有明显的变化，说明该方法能够很好地消除噪声对信号的影响，更好地判断信号的局部分布状况，因此相关性小波奇异熵可以应用于轴承故障信号的特征提取。

2.2 稳定性分析

通过对实际的轴承测量，对故障信号的稳定性进行分析。实验用的轴承为圆柱滚子轴承N205，轴承参数为：转速1 200r/min，频率40Hz，采样数8 192点。故障类型为滚动轴承的内圈故障、外圈故障和滚珠故障，其轴承故障信号如图2所示。对轴承的4种故障信号各做40次实验，然后为每种故障信号的40组数据进行相关性小波奇异熵计算，得到部分熵值见表2。

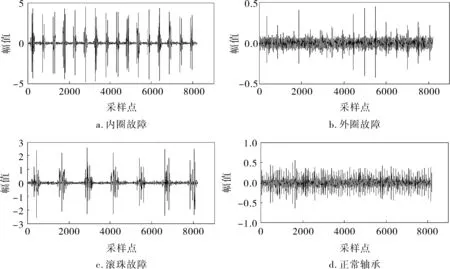
图2 轴承故障信号

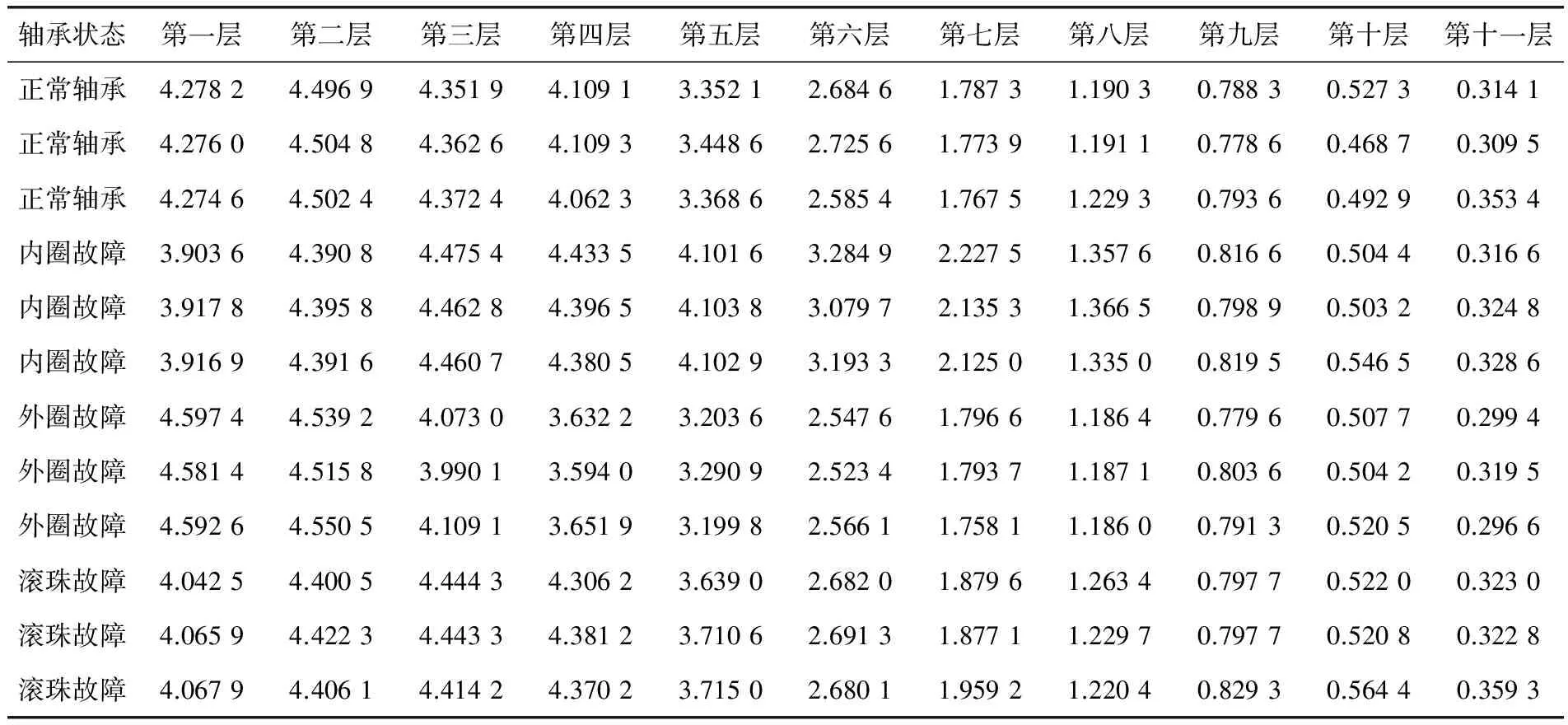
轴承状态第一层第二层第三层第四层第五层第六层第七层第八层第九层第十层第十一层正常轴承4．27824．49694．35194．10913．35212．68461．78731．19030．78830．52730．3141正常轴承4．27604．50484．36264．10933．44862．72561．77391．19110．77860．46870．3095正常轴承4．27464．50244．37244．06233．36862．58541．76751．22930．79360．49290．3534内圈故障3．90364．39084．47544．43354．10163．28492．22751．35760．81660．50440．3166内圈故障3．91784．39584．46284．39654．10383．07972．13531．36650．79890．50320．3248内圈故障3．91694．39164．46074．38054．10293．19332．12501．33500．81950．54650．3286外圈故障4．59744．53924．07303．63223．20362．54761．79661．18640．77960．50770．2994外圈故障4．58144．51583．99013．59403．29092．52341．79371．18710．80360．50420．3195外圈故障4．59264．55054．10913．65193．19982．56611．75811．18600．79130．52050．2966滚珠故障4．04254．40054．44434．30623．63902．68201．87961．26340．79770．52200．3230滚珠故障4．06594．42234．44334．38123．71062．69131．87711．22970．79770．52080．3228滚珠故障4．06794．40614．41424．37023．71502．68011．95921．22040．82930．56440．3593

从表2中的相关性小波奇异熵值可以看出，内圈故障、外圈故障、滚珠故障和正常轴承的奇异熵值处于不同的数值范围内，有明显的区分度。每种轴承故障信号相关性小波奇异熵没有明显的变化，说明该方法所得的特征矢量相对比较稳定。

3 基于概率神经网络的故障分类

概率神经网络(Probabilistic Neural Networks，PNN)是吸收了径向基函数网络和经典的概率密度估计的优点发展而来的一种前馈型神经网络。其理论依据是叶斯最小风险准则，概率神经网络是一种径向神经网络，适合于模式分类。由于概率神经网路模型具有非线性分类能力，可以将故障样本空间映射到故障模式空间中，因此可形成一个具有较强容错能力、结构自适应能力的网络系统，从而提高故障特征提取的准确率。

PNN由输入层、模式层、求和层和输出层4部分组成。其中训练样本的值送给输入层，将特征向量传送给网络，其神经元个数和样本向量的维数是一样的。模式层计算来自输入的故障信号的特征向量与训练样本中各个类型的匹配关系，模式层神经元的数目等于各个类型所有的训练样本数，该层每个模式部分的输出如下：

(13)

其中，W为从第一层到第二层的连接权值，等于输入向量的转置；δ为平滑因子，在分类中起着非常重要的作用。

第三层是求和层，是将属于某种类型的概率累计，按式(13)计算，可以得到故障模式的估计概率密度函数。求和层单元的输出与各类基于内核的概率密度的估计成比例，通过输出层即最后一层的归一化处理，能够得到各种类型的概率估计。网络的输出层决策由简单的阈值辨别器组成，输出层神经元是一种具有竞争能力的神经元，每个神经元分别对应于一种故障模式，神经元的个数相当于训练样本数据的类型个数。

在组建神经网络模型中，选用的特征向量都必须能够正确反映样本信号的特征信息。本实验共采集了160个样本数据，每种类型40个，其中20个作为训练样本，20个作为测试样本。利用相关性小波奇异熵计算，将熵值作为特征向量输入到概率神经网络中进行分类，分类结果见表3。

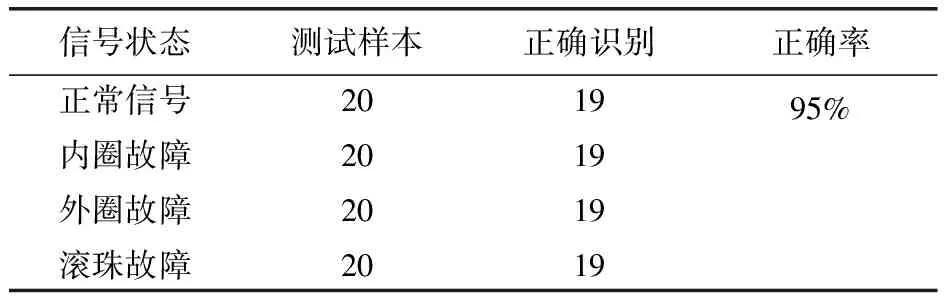
表3 概率神经网络分类结果

4 结束语

随着现代化工业自动化程度的日益提高，故障诊断被广泛地应用在机械设备中，而特征提取是故障诊断的重要部分。笔者提出了将小波变换、相关性、奇异值分解和信息熵理论结合在一起，用于对滚动轴承故障信号进行特征提取。通过实验测试表明，该方法具有良好的容噪能力和稳定性，能够准确地提取故障信号的特征。同时，利用概率神经网络对滚动轴承故障信号进行分类，该方法简单、识别率高。但是由于实验室采集到的轴承运动状态比较简单，而且故障较为明显。因此，对于复杂的运行环境下对滚动轴承故障信号的特征提取还有待进一步研究。

[1] Southard L,Hoeg T M,Palmer D W,et al.Exploring Mars Using a Group of Tumbleweed Rovers[C].2007 IEEE International Conference on Robotics and Automation.Roma：IEEE,2007：775～780.

[2] 孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005.

[3] 赵学智,叶邦彦,陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J].机械工程学报,2010,46(1):100～108.

[4] 杨宇,于德介,程军圣.基于EMD的奇异值分解技术在滚动轴承故障诊断中的应用[J].振动与冲击,2005,24(2):12～15，145.

[5] 于德介,陈淼峰,程军圣,等.基于EMD的奇异值熵在转子系统故障诊断中的应用[J].振动与冲击,2006,25(2):24～26，34，181.

[6] 傅祖芸.信息论——基础理论与应用[M].北京：电子工业出版社，2001.