基于神经网络优化的永磁同步直线电机迭代学习位置控制方案

2015-01-13温阳东

化工自动化及仪表 2015年9期

汪昕林勇温阳东

(合肥工业大学电气与自动化工程学院,合肥 230009)

永磁同步直线电机(PMLSM)是一种将电能直接转换成直线运动机械能的传动装置，近年来在工业控制领域有着广泛的应用[1]。由于直线电机系统是一个多变量、时变的非线性系统，因此传统的PID算法对这类系统很难实现精确控制。

迭代学习(ILC)是一种新型控制算法，在给定时间内能以简单的学习算法实现对期望轨迹的高精度跟踪[2]。ILC可以处理系统中各种周期性的扰动，且不依赖于系统的精确模型[3]。ILC适合于某种重复运行性质的被控对象，可实现有限时间区间上的完全跟踪任务，因此对它的研究对直线电机的控制具有重要意义[4]。但是单纯的开环ILC算法具有局限性，其基本控制原理是利用系统当前运行产生的误差信息，修正其控制输入，以得到系统下次运行时的控制输入。王丹凤等提出了一种基于神经网络优化的ILC控制算法，但是该算法采用的仍是开环控制，对误差信息的利用不够充分[5]。白敬彩和吴君晓提出了一种开闭环ILC控制算法，但该算法是固定的学习速率，学习速度慢[6]。在此，笔者采用神经网络优化的开闭环P型ILC控制算法来控制PMLSM，以较快的收敛速度逼近期望位置轨迹，达到较理想的位置控制效果。

对PMLSM采用矢量控制方法，利用坐标变换，建立永磁同步电机在d-q坐标的数学模型，令d轴的参考电流id*=0，因此电磁力矩仅和q轴电流有关，便于控制。

PMLSM的机械运动模型可以描述为：

式中Ffric——摩擦力；

Fm——电磁推力；

Frip——推力脉动；

iq——q轴电流；

Kf——推力系数；

m——动子质量。

磁阻产生的脉动力模型Frip=bsin(ω0x)，x为位置[7]。完整的摩擦力模型通常很复杂，选用LuGre摩擦力数学模型[8]，即：

Ffric=[fc+(fs-fc)e-(v/vs)2]sgn(v)+Bv

式中B——粘滞摩擦系数；

fc——动摩擦力；

fs——静摩擦力；

sgn()——符号函数，其值由运动方向决定；

vs——润滑系数。

PMLSM的电压平衡模型为：

式中Ld、Lq——动子电枢d、q轴电感分量；

R——电枢电阻；

ψf——定子的磁链。

根据上述模型建立的控制系统模型如图1所示，为典型的三环控制结构，位置环采用ILC算法进行调节，速度环和电流环采用PI算法进行调节[9]。

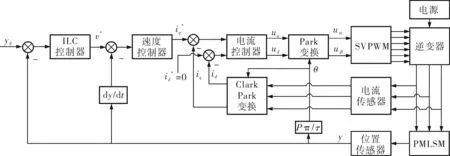
图1 控制系统模型

系统工作过程：ILC控制器根据期望位置数值与反馈值之差，得到速度的参考值，该参考值与实际速度值相比较后，将差值送入速度调节器，得到q轴参考电流值。由此可得到d、q轴电压值，经过坐标变换得到α和β轴的参考电压，并由电压空间矢量脉宽调制器(SVPWM)生成逆变器的驱动信号来控制电机。

2 控制方案

2.1 开环ILC算法

开环P型ILC的学习律为：

uk+1(t)=uk(t)+kpek(t)

式中ek(t)——第k次迭代的误差；

k——迭代次数；

kp——ILC的学习增益；

uk+1(t)——第k+1次的控制输入。

2.2 开闭环ILC算法

由于开环ILC只利用了系统前一次运行的信息，对当前运行的信息没有加以利用，所以对被控对象无镇定作用，本质上属于一种离线控制。因此笔者在开环ILC的基础上引入反馈，构成开闭环ILC。开闭环ILC的结构框图如图2所示，yd(t)为期望输出；yk(t)为实际系统输出。由图2可知，第k+1次控制系统的输入uk+1(t)由3部分组成：开环ILC控制提供的输入优化uff,k(t)，闭环ILC控制提供的输入优化ufb,k+1(t)，前一个迭代周期的输入uk(t)。因此开闭环P型ILC的学习律可表示为：

uk+1(t)=uk(t)+uff,k(t)+ufb,k+1(t)

其中，uff,k(t)=kopek(t)为开环控制学习律；ufb,k+1(t)=kcpek+1(t)为闭环控制学习律。

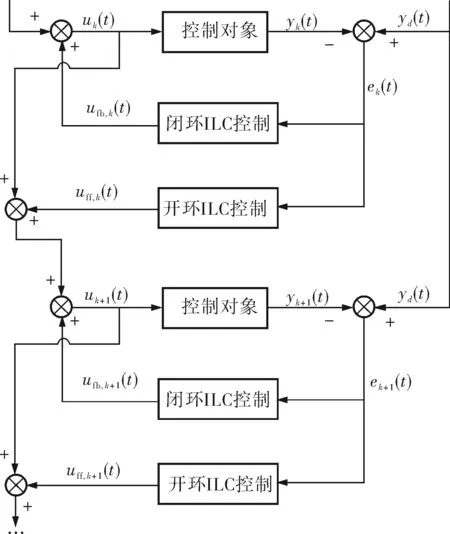
图2 开闭环ILC的结构框图

开闭环P型ILC控制算法既利用前一迭代周期的误差，也利用当前周期的输出误差作为迭代依据，经过多次迭代后位置误差可达到较小的范围[10]，理论上性能会优于开环ILC控制。

2.3 基于神经网络优化的开闭环ILC控制

径向基函数(RBF)神经网络是一种三层前向网络，包含输入层、隐含层和输出层。由输入到输出的映射是非线性的，但隐含层空间到输出层空间的映射是线性的，从而加快了学习速度且避免了局部极小值问题[11]。

采用RBF网络对反馈部分进行在线整定优化，即对kcp进行优化。神经网络选为3-6-1结构，网络的输入向量X=[u(n),y(n),y(n-1)]T，径向基向量H=[h1,h2,…,h6]T，其中hj为常用的高斯函数[12]，即：

根据梯度下降法，各参数的迭代算法如下：

wj(n)=wj(n-1)+Δwj(n)+α(wj(n-1)-

wj(n-2))

bj(n)=bj(n-1)+Δbj(n)+α(bj(n-1)-

bj(n-2))

cji(n)=cji(n-1)+Δcji(n)+α(cji(n-1)-

cji(n-2))

式中α——动量因子；

η——学习速率。

由梯度下降法得到kcp的调整量Δkcp为(η1为参数调整率)：

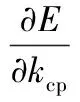
基于神经网络优化的ILC控制过程：在第k次迭代运行过程中，输入信号加入被控对象中，产生输出信号，RBF神经网络根据实时误差和开环调整量不断改变kcp，加快系统的收敛速度，直到误差满足条件或此次迭代过程结束。

3 仿真实例与分析

永磁直线电机的仿真参数设置：m=1.97kg，fc=10N，fs=20N，B=82.22N·s/m，vs=0.01，b=8.5N，ω0=100rad/s，Ld=Lq=82.6mH，R=0.2Ω，极距τ=36mm，ψf=0.15287Wb，速度环的PI参数分别为50、80。直线电机的初始位置和期望初始位置相同，期望位置轨迹yd(t)=-20(15t4-6t5-10t3)，t∈[0,1]。仿真时间1s，过程中采样周期设为0.001s，最大迭代次数20。

采用Matlab软件分别对开环P型ILC控制、开闭环P型ILC控制和神经网络优化的开闭环P型ILC控制算法的直线电机进行位置跟踪仿真。令开环ILC系数kp=20，开闭环ILC系数kop=20、kcp=25；同样令神经网络优化的ILC初始系数kop=20、kcp=25，神经网络的初始权值设为(-0.5,0.5)之间的随机数，学习速率η=0.15，参数调整率η1=0.5，动量因子α=0.05。位置最大跟踪误差随迭代次数的变化曲线如图3所示，不同迭代次数的最大误差绝对值见表1。

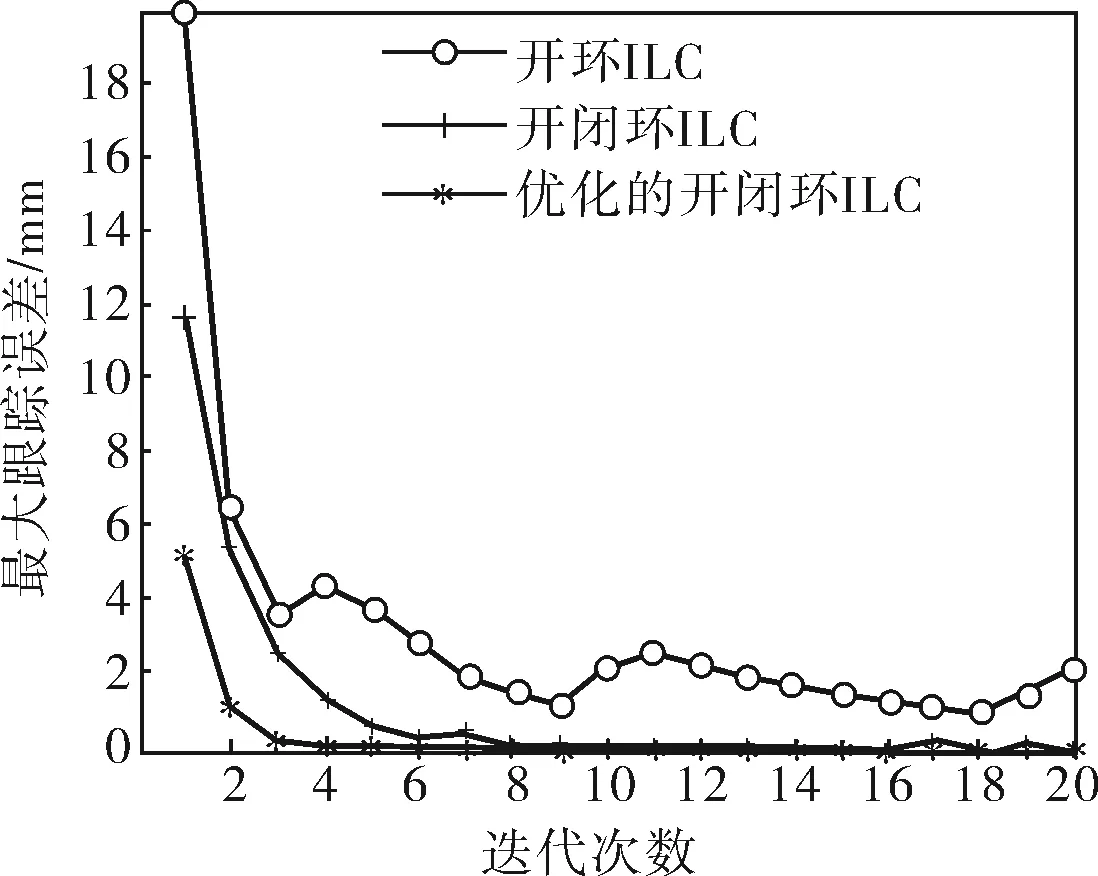
图3 位置最大跟踪误差随迭代次数的变化曲线

分析可以看出，随着迭代次数的增加，开闭环ILC控制的误差收敛速度相对于开环ILC控制有所加快，第20次迭代的最大位置误差下降为0.018 9mm；而神经网络优化的开闭环ILC控制误差的收敛速度进一步加快，第20次迭代的最大位置误差达到2.743 0×10-4mm，可见加入神经网络后误差变小且收敛速度明显加快。