基于Fisher KNMF的非线性多故障诊断方法

冉永清 李 楠 杨煜普

(上海交通大学电子信息与电气工程学院系统控制与信息处理教育部重点实验室，上海 200240)

传统的故障诊断方法根据监控统计量来检测是否有故障发生，采用贡献图及故障重构等方法来辨识故障发生的位置，以此达到故障诊断的目的[1，2]。然而这类方法都是基于过程中出现单一故障的假设，如果在检测过程中同时出现多个故障，这类方法的故障诊断性能将急剧下降。为解决上述问题，笔者从模式识别的角度考虑故障诊断问题，将故障诊断分为两个步骤，在离线状态下，学习数据之间的内部关系及模式等抽象概念，建立故障诊断模型；在在线状态下，所建立的故障诊断模型运用学习到的知识，对新数据的内在关系和模式做出预测，把故障数据分类到最接近的故障类中。从这个角度出发，笔者把故障诊断看成一个多类分类问题，提出了有监督学习方法——FKNMF方法，建立多故障诊断模型，解决多故障诊断问题。

KNMF算法通过核函数将输入空间的非线性数据映射到高维特征空间[3，4]，采用迭代的矩阵分解形式，挖掘特征空间数据的局部信息表示数据整体结构。令输入空间的数据X=[X1，X2，…,Xn]∈Rm×n，通过映射函数将数据映射到一个高维的特征空间F内，得到的特征空间数据矩阵Φ(X)=[Φ(x1),Φ(x2),…,Φ(xn)]∈Rd×n。在特征空间F内，寻找一个基矩阵U和一个系数矩阵V，使得Φ(·)：Rm→F:Rd：

Φ(X)≈UVT

(1)

其中U∈Rd×r，r表示降维后的维数；V∈Rn×r。

根据KNMF算法，假设基矩阵U是特征数据Φ(X)的凸组合，即U=Φ(X)W，则在特征空间F内，把特征空间数据分解成如下形式：

Φ(X)≈Φ(X)WVT

(2)

KNMF算法是在特征空间内通过学习寻找到参数矩阵W和系数矩阵V。

2 Fisher判据分析

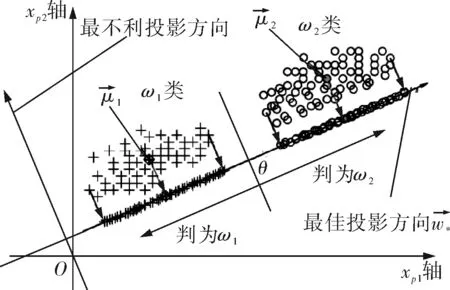
图1 Fisher判别的基本原理

以下为Fisher准则的若干个必要判别参数。

在d维空间内，各个样本均值向量mi：

(3)

样本类内离散度矩阵Si和总类内离散度矩阵Sw：

(4)

Sw=S1+S2

(5)

样本类间离散度矩阵Sb：

Sb=(m1-m2)(m1-m2)T

(6)

Fisher准则函数定义：

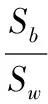
(7)

在特征空间里面，各个样本在特征空间上的投影：

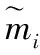
(8)

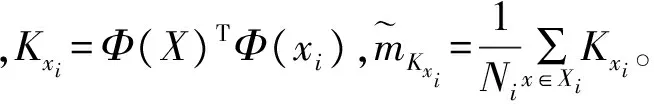
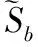
(9)

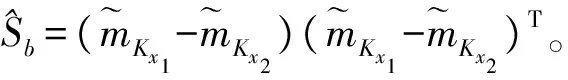
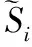
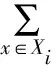
(10)

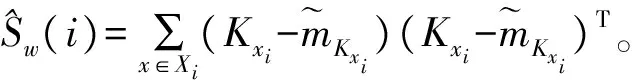
(11)

根据式(7)的定义可得：

(12)

由式(12)可见，在特征空间中，Fisher准则就是寻找使JF(w)最大的参数矩阵W，使各类样本尽可能地分开，同时同一样本尽量靠拢。

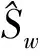
(13)

3 Fisher KNMF算法

笔者结合KNMF和FDA两者的优点，使KNMF算法在降维过程中，引入FDA分类思想，使得降维过程中同一类的数据尽量靠拢，不同类的数据尽量远离。这样既保持了KNMF算法挖掘局部信息的能力，综合了FDA的优点，也弥补了FDA分类算法过度依赖数据均值的缺点。

3.1 目标函数的建立

在特征空间内，采用欧式距离来度量特征数据矩阵Φ(X)与Φ(X)、参数矩阵W和系数矩阵V三者乘积之间的误差，将KNMF问题转化为求取参数矩阵W和系数矩阵V，并使得以下目标函数取得最小值：

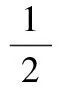
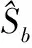
(14)

其中ε是任意的极小值，该限制的含义是使式(13)尽可能相等。

将式(14)转化成下列形式：

(15)

式(15)表示Fisher KNMF算法在KNMF算法的框架上增加了FDA分类思想作为正则项，其中参数α是一个系数，通过调节它来调整Fisher正则项的影响程度，使Fisher KNMF算法具有良好的灵活性。

3.2 目标函数求解

目标函数式(15)对于W和V单个变量是凸函数，但是同时对两个变量是非凸函数，对于目标函数求取的解可能不是全局最优解。根据式(15)的KKT最优松弛条件和互补松弛条件可以得到：

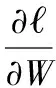
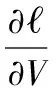
(16)

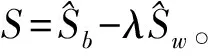
根据式(16)得到W、V和λ的更新规则：

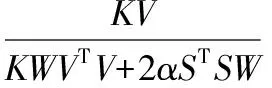
(17)

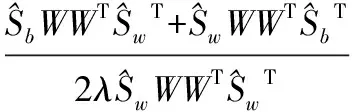
采用式(17)的更新规则，最终可以得到FKNMF算法的参数矩阵W和系数矩阵V。

4 基于Fisher KNMF的多故障诊断方法

Fisher KNMF算法从一个包含正常数据和故障数据的训练数据集中通过迭代矩阵分解，获得参数矩阵W。对于未知类别的样本，需要一个判别函数值来量化观测向量和类之间的关系。观测向量xi在类K上面的判别函数值采用下面判别式[6]：

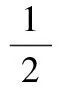
(18)

其中pk是第K类的概率。

对于每一个测试样本xt，通过式(18)计算出它在每一类上的判别值，然后判断该样本属于判别函数值最大的那一类。即：

(19)

如果训练样本中只有正常数据和一种故障数据，即故障检测；如果训练数据包含了多种故障数据，那么在建立模型之后，就可以对测试样本进行故障诊断，判别该样本处于正常状态或是哪一类故障状态，即完成了多故障诊断。

5 仿真实验

TE过程是基于实际工业过程的仿真案例[8]，整个过程系统共包括12个控制变量和41个测量变量，并且预定了21种故障。图2为TE过程结构图。

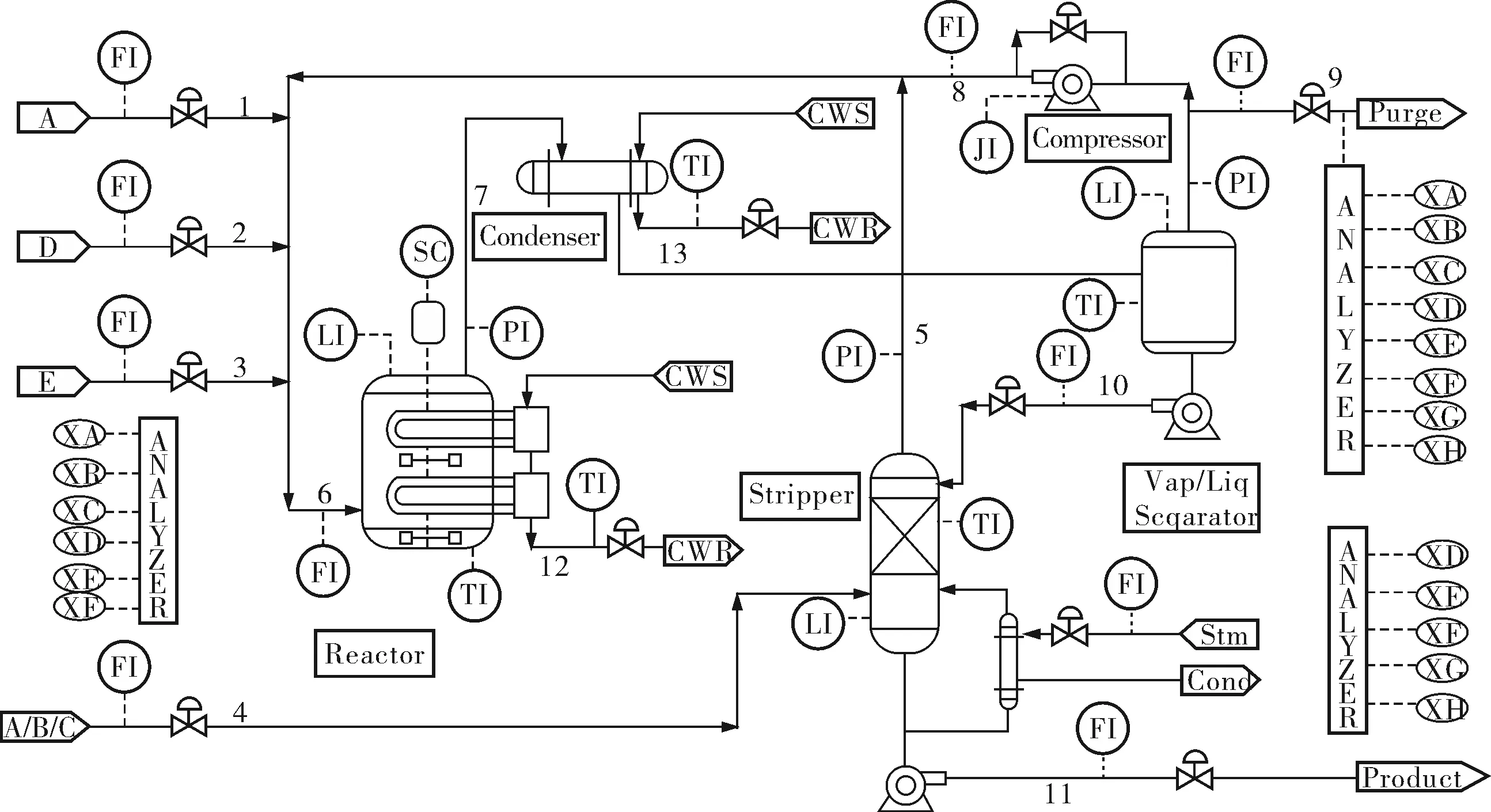
图2 TE过程结构图

5.1 单故障的诊断情况

选取正常数据的前200个数据和故障数据的201～400之间的200个数据共同作为训练数据，选取正常数据的281～480之间的200个数据和故障数据81～280之间的200个数据作为测试数据。设置降维维数为17，取系数α为0.5。表1是FDA算法和Fisher KNMF算法故障诊断准确率对比。

表1 FDA算法和Fisher KNMF算法故障诊断准确率对比 %

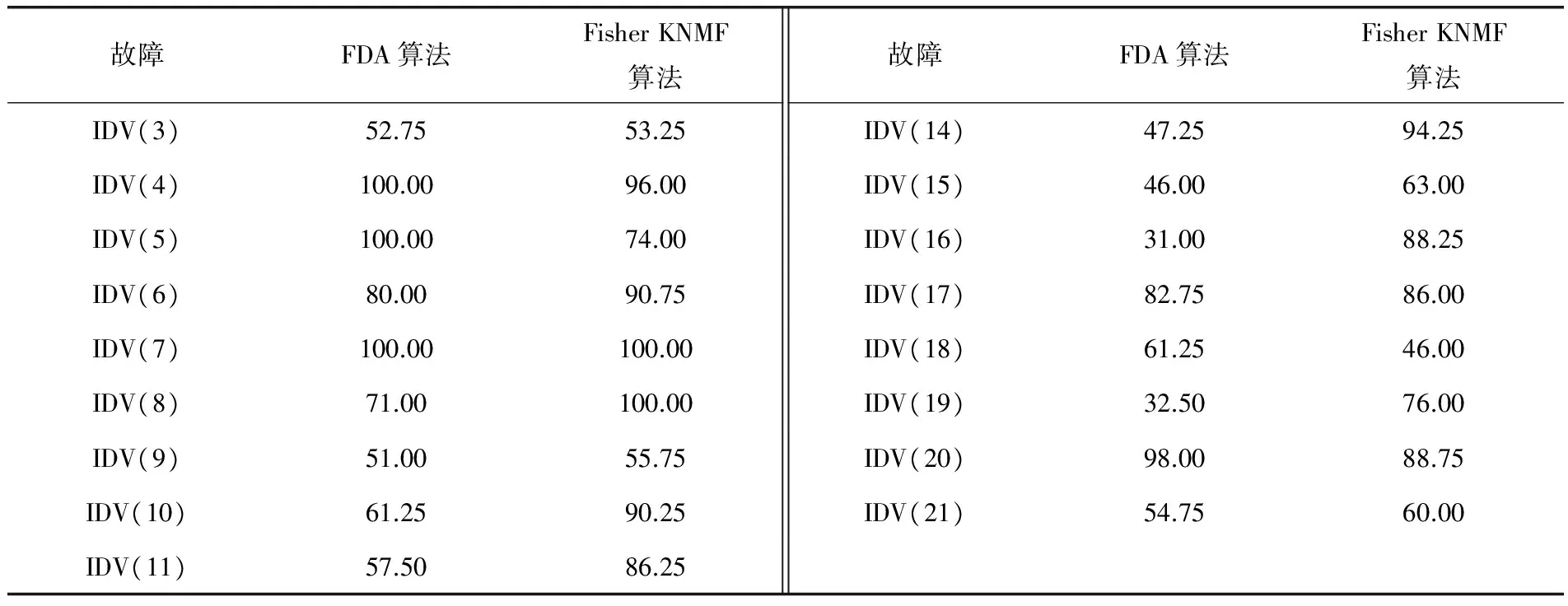
(续表1)

从表1可以看出，Fisher KNMF算法的故障诊断准确率总体上是优于FDA算法的，其中在故障IDV(8)、IDV(10)、IDV(11)、IDV(12)、IDV(14)、IDV(16)和IDV(19)发生时，Fisher KNMF算法的故障诊断准确率明显优于FDA算法。图3是IDV(1)和IDV(14)的FDA算法和Fisher KNMF算法的诊断效果图。FDA算法故障诊断效果图横坐标1～200表示两类故障都为200个点，故障IDV(1)和IDV(14)的纵坐标如果差距越大分的就越开，Fisher KNMF算法纵坐标表示两类故障的个数，前200个应该是正常数据，后200个是故障数据。从图3可以得知，在故障IDV(1)发生时，FDA和Fisher KNMF算法都能够完全分开故障，但是在故障IDV(14)发生时，FDA算法不能完全分开故障类别，而Fisher KNMF算法依然有94.25%的准确率。

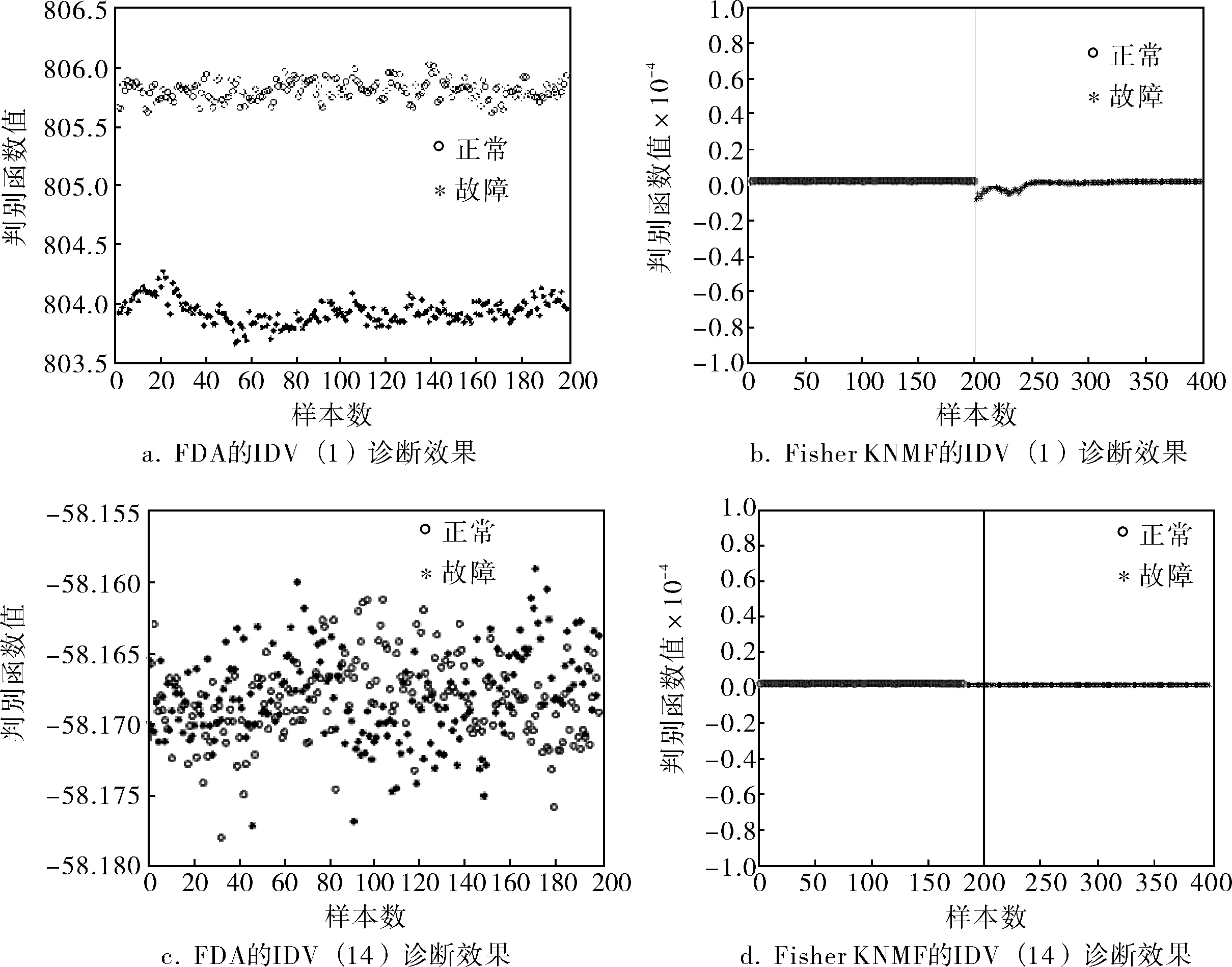
图3 IDV(1)和IDV(14)发生时，FDA和Fisher KNMF算法的故障诊断效果

5.2 多故障的诊断情况

采用正常数据和两种故障训练数据来进行仿真实验。取正常数据和两类故障训练数据分别为200个数据，同样每类测试集各选取200个点组成。仿真实验中，设置降维维数为17，系数α为0.5。图4是IDV(10)和IDV(14)同时发生时FDA算法和Fisher KNMF算法的故障诊断效果图。

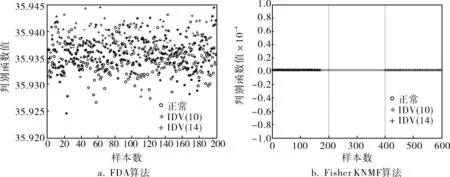
图4 IDV(10)和IDV(14)同时发生时，FDA和Fisher KNMF算法的故障诊断效果

图4中FDA算法基本不能分出3类数据，但是Fisher KNMF算法能够达到93.25%的诊断正确率，仅有少数数据标识错误，通过此仿真实例说明，Fisher KNMF算法在多类故障诊断中具有很好的性能。

6 结束语

为解决多故障诊断问题，笔者从模式分类的新角度考虑，提出了一种新的有监督分类方法——Fisher KNMF算法，该算法结合了KNMF算法优秀的处理非线性数据的能力和FDA算法优秀的分类能力。建立的多故障诊断模型用于在线监控，并在TE模型上仿真，结果表明：在单故障和多故障的情况下都具有很好的效果。

[1] 王迎，王新明，赵小强.基于小波去噪与KPCA的TE过程故障检测研究[J].化工机械，2011,38(1):49～53.

[2] 唐友福，刘树林，刘颖慧，等.基于α稳定分布的往复压缩机故障诊断方法[J].化工机械，2011,38(5):555～558.

[3] Lee H,Cichocki A,Choi S.Kernel Nonnegative Matrix Factorization for Spectral EEG Feature Extraction[J].Neurocomputing,2009,72(13-15):3182～3190.

[4] 李巍华.基于核方法的机械故障特征提取与分类技术研究[D].武汉：华中科技大学，2003.

[5] Chiang L H,Kotanchek M E,Kordon A K.Fault Diagnosis Based on Fisher Discriminant Analysis and Support Vector Machines[J].Computers & Chemical Engineering,2004,28(8):1389～1401.

[6] 李祥宝.基于广义非负矩阵投影算法的故障检测与诊断研究[D].上海：上海交通大学，2014.

[7] 何晓斌.基于统计学方法的自适应过程监控与故障诊断[D].上海：上海交通大学,2008.

[8] Yoon S,MacGregor J F.Fault Diagnosis with Multivariate Statistical Models Part I:Using Steady State Fault Signatures[J].Journal of Process Control,2001,11(4):387～400.