拟静力分量对列车-轨道-桥梁系统地震响应的影响

雷虎军， 李小珍

(西南交通大学土木工程学院，四川 成都610031)

我国位于世界两大地震带——环太平洋地震带和亚欧地震带之间，是全球大陆地震最活跃的地区之一.地震除引起桥梁结构本身破坏外，对桥上列车行车安全性的影响不容忽视.如在日本新潟地震中就曾发生过运行于高架桥上的新干线列车脱轨的事故，造成了惨重的人员伤亡和经济损失.

近年来，不少学者针对地震作用下桥上列车的行车安全问题进行了广泛研究. 其中，在地震力输入方法上大体可分为2 类，一类是忽略结构的拟静力分量，只考虑地震力引起的动力分量，在相对坐标系下求解.夏禾、邓子铭、熊建珍、韩艳、王少林等均采用相对运动法输入地震力，忽略结构拟静力分量的影响，研究了地震作用下不同结构桥梁上列车的行车安全性［1-5］;另一类是同时考虑地震力引起的动力分量和拟静力分量，在绝对坐标系下求解.张楠等采用大质量法研究了多点激励下车桥系统的地震响应［6］;YANG Y B 等采用直接求解法研究了地震发生时高速列车通过简支梁桥的稳定性［7］;杜宪亭等分别采用直接求解法和相对运动法求解车桥系统的地震响应，比较了位移输入模式和加速度输入模式对车桥系统地震响应的影响［8］.

传统的桥梁抗震更关注力，与相对位移有关，结构拟静力分量的影响有限.而地震作用下车桥耦合振动的研究更关注车辆的行车安全性，与绝对位移有关，此时需要探讨结构拟静力分量的影响. 因此，研究结构拟静力分量的影响对在车桥系统中正确输入地震力具有重要意义.然而，到目前为止，还鲜有针对列车-轨道-桥梁系统研究结构拟静力分量影响的报道.

本文在已有研究［9-11］的基础上，根据列车-轨道-桥梁动力相互作用理论，考虑路基和桥梁地震力边界条件，分别采用相对运动法和大质量法，在相对坐标系和绝对坐标系下处理地震力边界条件，建立了不同坐标系下的列车-轨道-桥梁系统地震响应分析模型，并以某跨度48 m+5 ×80 m+48 m的刚构-连续组合梁桥为例，分别探讨了结构单向和三向拟静力分量对系统地震响应的影响.

1 列车-轨道-桥梁系统地震响应分析模型

地震作用下的列车-轨道-桥梁耦合振动模型是由车辆模型、轨道模型和桥梁模型在轮轨接触界面处、线桥接触界面处分别通过动态轮轨关系和桥轨关系相关联的耦合时变系统，其自激激励源为轮轨间的几何不平顺，外部激励源为作用于地面支撑点的地震激励.由地震荷载的作用机理可知，只要与地面接触的部分均要直接承受地震力. 因此，列车-轨道-桥梁系统的地震力边界条件应包含路基地震力边界条件和桥梁地震力边界条件，见图1.

图1 地震作用下列车-轨道-桥梁耦合振动模型Fig.1 Dynamic model of train-track-bridge coupling system subjected to an earthquake

车辆采用35 个自由度的四轴机车车辆模型，轨道采用三层弹性点支撑梁有砟轨道模型，桥梁采用空间杆系有限元模型，动力学模型及运动方程见文献［12］.通过推导，在地震作用下，列车-轨道-桥梁耦合振动方程为

式中:下标v、t 和b 分别代表车辆、轨道和桥梁子系统;M、C 和K 分别为质量、阻尼和刚度矩阵;u、和分别为位移、速度和加速度列向量;Ptv和Pvt分别为车辆子系统与轨道子系统间的作用力和反用力;Ptb和Pbt分别为桥梁子系统与轨道子系统间的作用力和反作用力;Pgt为基础作用于轨道的地震力;Pgb为基础作用于桥梁的地震力.

假设轮轨刚性接触，并允许发生脱离，轮轨法向接触力采用Hertz 非线性弹性接触理论求解，轮轨切向作用力采用Kalker 线性蠕滑理论求解，并通过Johnson-Vermeulen 理论进行非线性修正［13］.

将轨道子系统和桥梁子系统的所有自由度分别按地面支撑节点和非支撑节点分块，则在绝对坐标系下轨道子系统的运动方程为

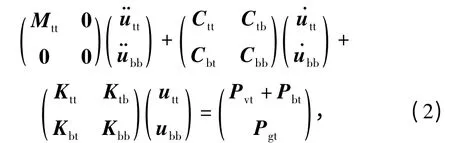
式中:下标tt 代表轨道子系统的非支撑节点自由度项，bb 代表地面支撑节点自由度项，tb 和bt 代表地面支撑节点自由度与非支撑节点自由度之间的相互影响项.

同样，桥梁子系统的运动方程为

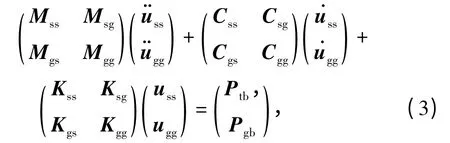
式中:下标ss 代表桥梁子系统的非支撑节点自由度项，gg 代表地面支撑节点自由度项，sg 和gs 代表地面支撑节点自由度与非支撑节点自由度之间的相互影响项.

以下分别采用大质量法和相对运动法处理列车-轨道-桥梁耦合系统的地震力边界条件.

1.1 大质量法处理地震力边界条件

大质量法是一种求解结构非一致地震响应的近似方法，它通过质量矩阵的置大数，巧妙地将地震荷载输入结构，其基本原理见文献［14］.采用大质量法处理列车-轨道-桥梁耦合系统的地震力边界条件时，轨道和桥梁子系统的运动方程分别变为

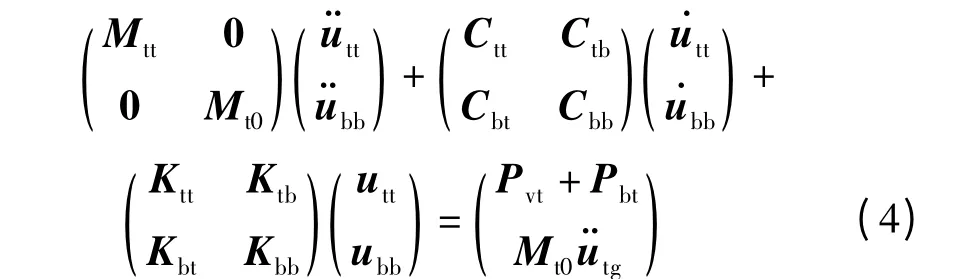
和

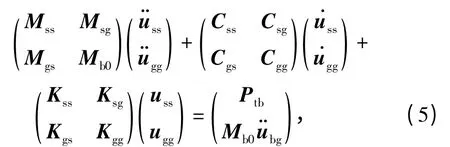
式中:Mt0为轨道子系统的大质量矩阵，附加大质量取轨道子系统总质量的108倍tg为输入路基支撑点的地震加速度时程;Mb0为桥梁子系统的大质量矩阵，附加大质量取桥梁子系统总质量的108倍;为输入桥梁支撑点的地震加速度时程.

式(4)和(5)即为绝对坐标系下考虑结构拟静力分量影响时轨道和桥梁子系统的运动方程，通过输入地震波加速度时程，联立车辆运动方程即可求出考虑结构拟静力分量时耦合系统的地震响应.

1.2 相对运动法处理地震力边界条件

相对运动法是人为将系统响应分为拟静力部分和动力部分分别求解，然后通过叠加获得系统的总响应.然而，考虑到轨道子系统可能存在非线性因素，此时叠加原理不再适用.因此，采用相对运动法输入地震力时进行如下简化:(1)忽略桥梁结构拟静力分量的影响;(2)忽略左、右侧路基支撑点传递给轨道系统的地震力. 由此，轨道子系统的运动方程可简化为

对于桥梁子系统，将结构的绝对位移分解为动位移和拟静力位移之和:

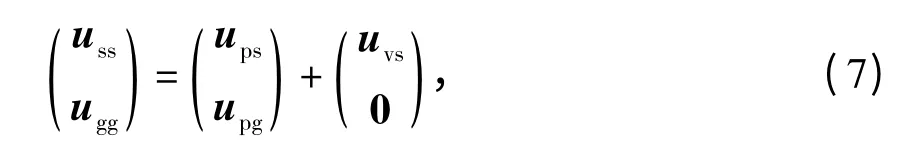
式中:ups和uvs分别为结构非支撑节点的拟静力位移分量和动位移分量;upg为结构支撑点处的基础位移，对于确定的地震动，upg已知.

根据相对运动法的基本理论，将式(7)代入式(3)，并假设采用集中质量矩阵和Rayleigh 阻尼模型，化简可得

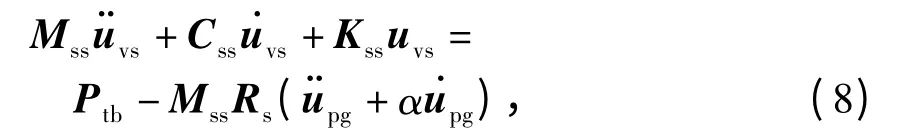
式中:Rs为影响矩阵，表示支撑节点自由度发生单位位移时在非支撑节点自由度处引起的位移;α 为质量阻尼系数.

式(6)和(8)即为相对坐标系下不考虑结构拟静力分量影响时轨道和桥梁子系统的运动方程，联立车辆运动方程即可求出不考虑结构拟静力分量时耦合系统的地震响应.

本文在原有列车-轨道-桥梁仿真分析程序［11］的基础上，按照上述2 种地震力边界条件处理方法，分别编制了大质量法和相对运动法地震力输入模块，用于研究结构拟静力分量对列车-轨道-桥梁系统地震响应的影响.

2 计算参数

以某跨度为48 m+5 ×80 m+48 m 的刚构-连续组合梁桥为分析对象，设计时速为300 km/h，双线，桥址位于Ⅰ类场地，总体布置见图2.主梁采用单箱单室变截面箱梁，桥面宽12.2 m，中间支点处梁高7.0 m，中跨跨中和边跨端部梁高4.0 m.

采用空间杆系有限元模型进行仿真计算，主梁和桥墩均采用空间梁单元模拟，活动墩墩顶与主梁形心通过主从自由度连接，刚构墩墩顶与主梁形心通过刚臂固结，不考虑地基刚度的影响，墩底边界按刚性固结处理，二期恒载取144.0 kN/m，结构阻尼比取2%.

轨道模型采用有砟轨道，列车模型采用ICE3高速列车，按16 辆车编组，轨道参数和列车参数见文献［15］.耦合系统时域积分步长取0.1 ms，轨道不平顺按德国低干扰轨道谱模拟.

计算时，为避免路基与桥梁界面轨道位移突变使该处车辆动力响应失真，在刚构-连续组合梁桥两侧各设置1 跨长32 m 的预应力混凝土箱梁作为过渡段与路基相连.

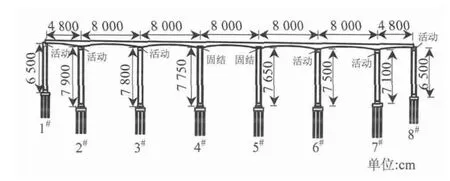
图2 刚构-连续组合梁桥总体布置Fig.2 Layout of a rigid-continuous girder bridge

以典型地震记录San Fernando (1971-02-09 14:00)地震的水平分量L09291 作为输入，记录台站为127 Lake Hughes #9. 原始数据来自太平洋地震工程研究中心网站(http://peer. berkely. edu)，且已经过基线调整和带通滤波处理，通频带宽为0.5 ～25.0 Hz，可直接用于多点激励分析. 输入地震波加速度时程ag见图3.

图3 输入地震波时程Fig.3 Input seismic wave time history

3 结果分析

3.1 单向拟静力分量的影响

首先将San Fernando 地震波分别沿纵向、横向和竖向单独输入，考察结构单向拟静力分量对列车-轨道-桥梁系统地震响应的影响.采用建立的分析模型，计算了列车以300 km/h 的设计时速过桥时列车-轨道-桥梁系统的地震响应，响应幅值见表1 ～3(相对误差为考虑与不考虑结构拟静力分量时计算结果的相对误差).

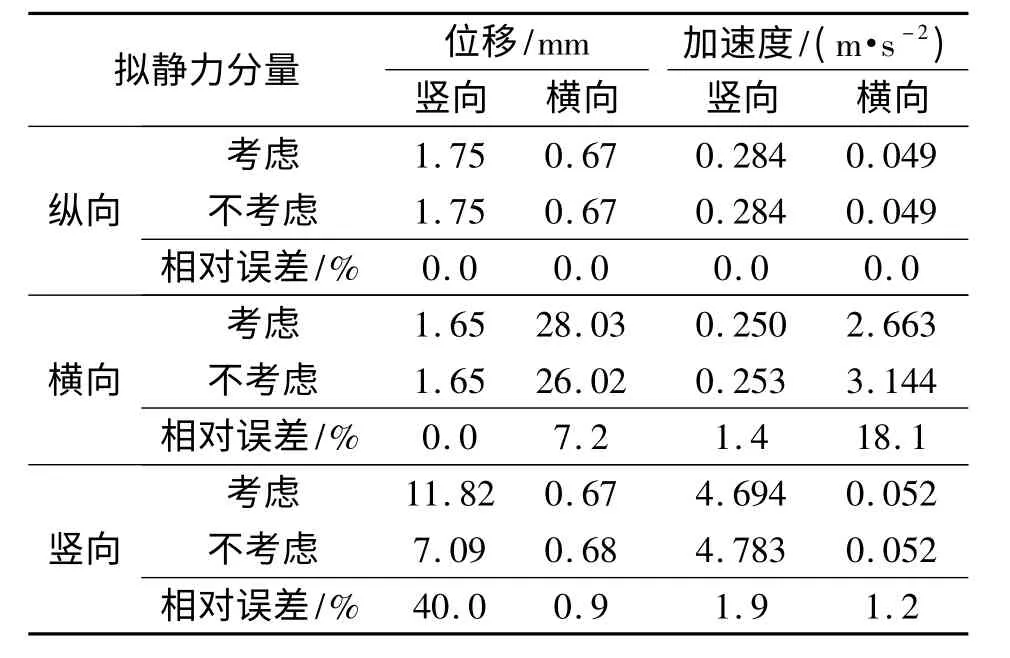
表1 桥梁动力响应幅值Tab.1 Dynamic response amplitudes of the bridge

从表1 可见:(1)桥梁纵向拟静力分量对其竖、横向位移和竖、横向加速度均无影响;(2)桥梁横向拟静力分量对其横向位移和横向加速度影响较大，而对桥梁竖向位移和竖向加速度几乎无影响.考虑桥梁横向拟静力分量时，桥梁的横向位移增大、横向加速度减小;(3)桥梁竖向拟静力分量对其竖向位移影响较大，而对横向位移和竖、横向加速度影响较小. 考虑桥梁竖向拟静力分量时，桥梁的竖向位移显著增大.

从表2 可见:(1)桥梁纵向拟静力分量对跨中截面钢轨的竖、横向位移以及车体竖、横向加速度均无影响;(2)桥梁横向拟静力分量对钢轨的竖向位移和车体竖向加速度几乎无影响，但使得横向位移和横向加速度显著增大;(3)桥梁竖向拟静力分量对钢轨的横向位移和车体横向加速度几乎无影响，而使钢轨竖向位移和车体竖向加速度增大.

从表3 可见，桥梁纵向和竖向拟静力分量对列车脱轨系数、轮重减载率和轮轨横向力几乎无影响，而横向拟静力分量使脱轨系数、轮重减载率和轮轨横向力均显著增大.

表2 钢轨位移和车体加速度幅值Tab.2 Displacement amplitudes of rail and acceleration amplitudes of car body

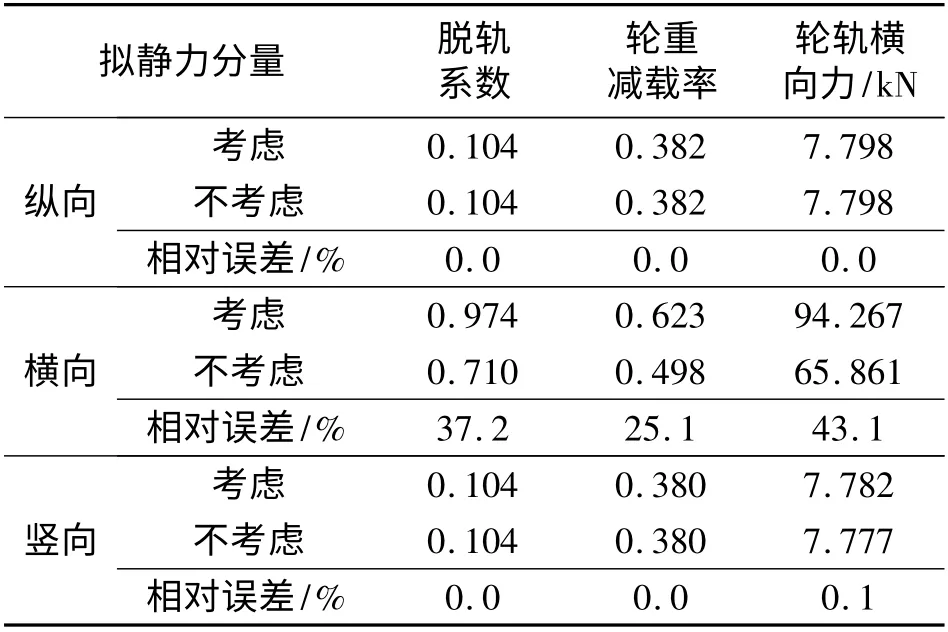
表3 列车行车安全性指标幅值Tab.3 Running safety index amplitudes

综上所述，结构拟静力分量对地震作用下列车-轨道-桥梁耦合系统动力响应的影响较大，且不同方向分量对不同动力响应指标的影响不同:

(1)桥梁纵向拟静力分量对列车-轨道-桥梁耦合系统的动力响应指标均无影响. 这是因为，耦合系统中车辆和轨道模型均未考虑纵向自由度，桥梁与轨道和车辆子系统在纵向无相互作用，纵向拟静力分量无法通过桥梁影响轨道和车辆子系统.因此，当仅研究纵向地震作用下列车-轨道-桥梁系统的动力响应时，可不考虑桥梁纵向拟静力分量的影响.

(2)桥梁横向拟静力分量将增大桥梁与钢轨横向位移、脱轨系数、轮重减载率和轮轨横向力等动力响应指标.因此，桥梁的横向拟静力分量对桥梁、轨道、车辆振动以及桥上列车的行车安全性影响最大，不考虑桥梁的横向拟静力分量可能严重低估车桥系统的动力响应.

(3)桥梁竖向拟静力分量仅影响车辆、轨道和桥梁的竖向动力响应指标，且对列车行车安全性指标的影响较小.因此，若不考虑桥梁竖向拟静力分量，将使计算得到的桥梁竖向位移、竖向加速度和钢轨竖向位移偏小.

3.2 三向拟静力分量的影响

进行实际结构的地震响应分析时，通常3 个方向的地震波分量均不可忽略. 因此，将 San Fernando 地震波沿纵向、横向和竖向同时输入，考察结构三向拟静力分量对列车-轨道-桥梁耦合系统地震响应的影响. 分别计算了高速列车以200、250、300 和350 km/h 的速度过桥时列车-轨道-桥梁系统的地震响应.图4 为三向地震波作用下高速列车以设计时速300 km/h 过桥时桥梁跨中截面动力响应的时程曲线.

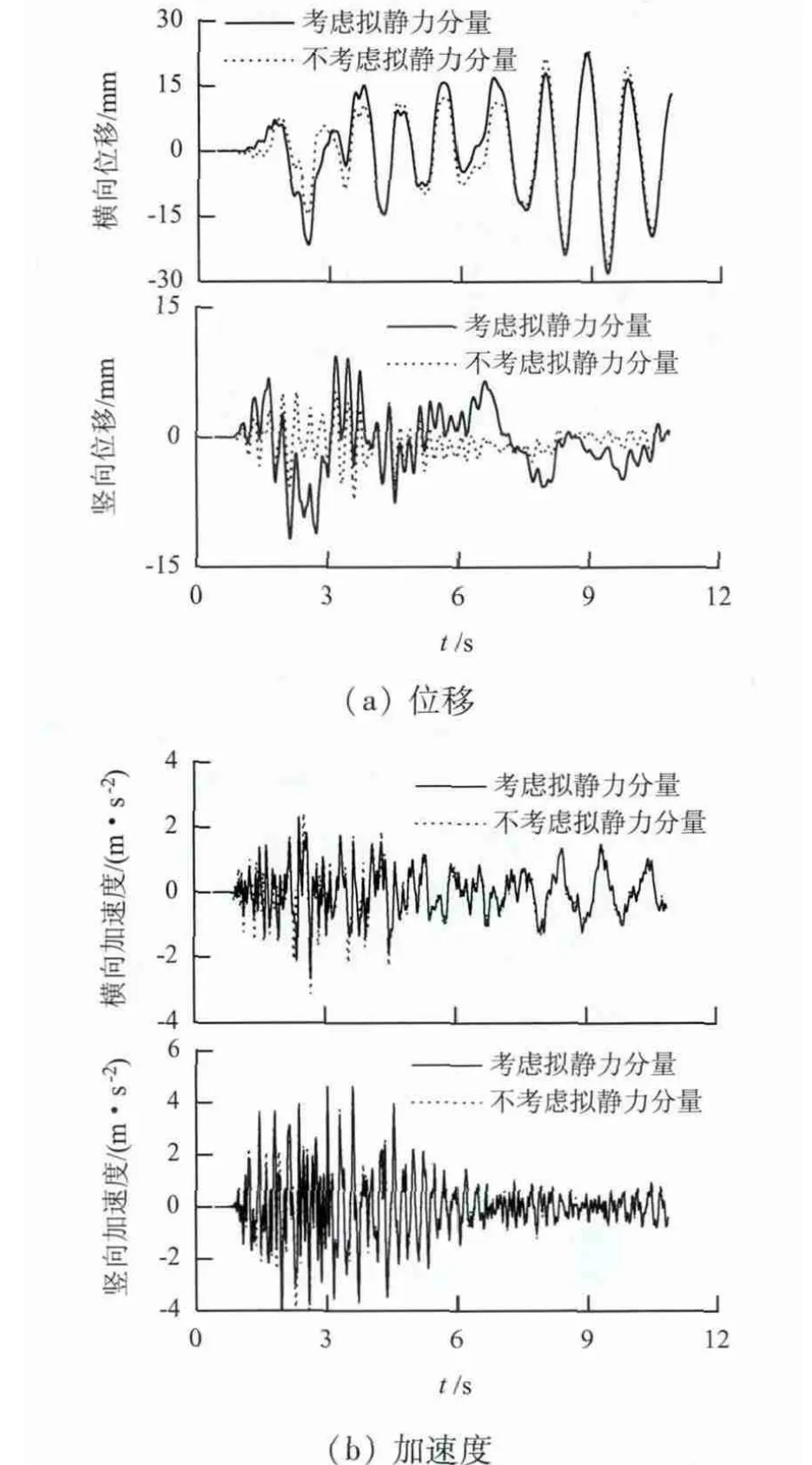
图4 桥梁动力响应时程Fig.4 Dynamic responses time-histories of the bridge

从图4 可见，考虑结构拟静力分量时，竖、横向位移时程完全不同于不考虑时的计算结果，且波形有差异;而竖、横向加速度时程与不考虑时的波形相似，但幅值有差异，考虑拟静力分量时的幅值小.

桥梁跨中位移、加速度、钢轨位移、车体加速度和列车行车安全性指标幅值随车速的变化分别见图5 ～9(百分数表示考虑与不考虑结构拟静力分量时计算结果的相对误差).

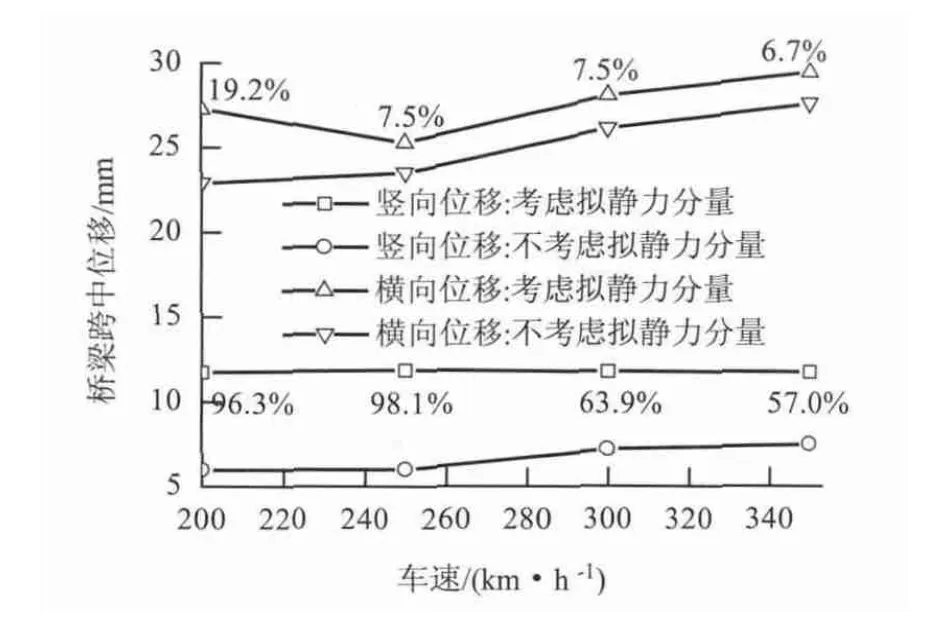
图5 桥梁位移幅值随车速的变化Fig.5 Displacement amplitudes of the bridge vs. train speed

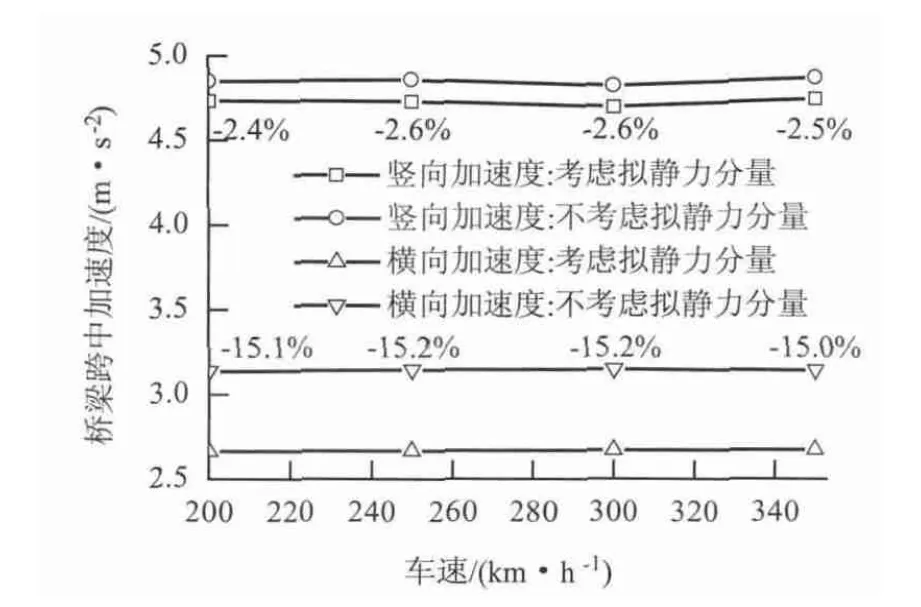
图6 桥梁加速度幅值随车速的变化Fig.6 Acceleration amplitudes of the bridge vs. train speed

从图5 和图6 可见，考虑结构拟静力分量时:(1)桥梁的竖、横向位移增大，相对误差随列车速度提高而减小.在计算列车速度范围内，竖、横向位移的最大相对误差分别为96.3% 和19. 2%;(2)桥梁的竖、横向加速度减小，相对误差随列车速度提高变化不大.在计算列车速度范围内，竖、横向加速度的最大相对误差分别为2.6%和15.2%.可见，结构拟静力分量会增大桥梁的振动位移，降低桥梁的振动加速度.

从图7 可见，考虑结构拟静力分量时，钢轨的竖、横向位移均大于不考虑时，且竖向位移的相对误差随列车速度提高而减小，而横向位移的相对误差随列车速度提高而增大. 在计算列车速度范围内，跨中钢轨竖、横向位移的最大相对误差分别为73.1%和21.2%.可见，结构拟静力分量会增大钢轨的振动位移，使钢轨振动加剧.

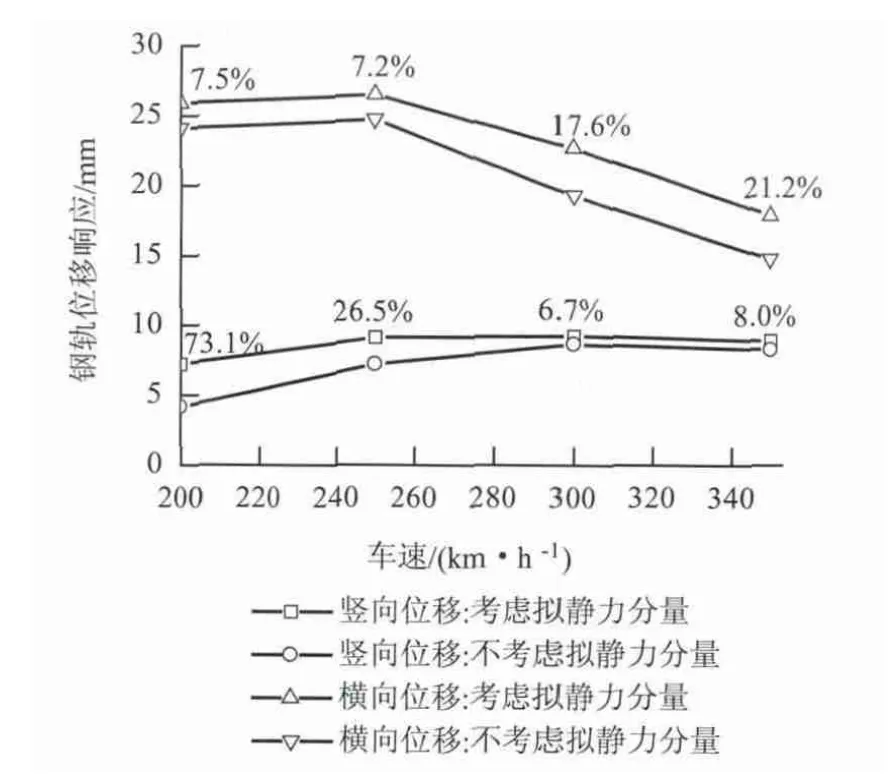
图7 钢轨位移幅值随车速的变化Fig.7 Displacement amplitudes of rail vs. train speed

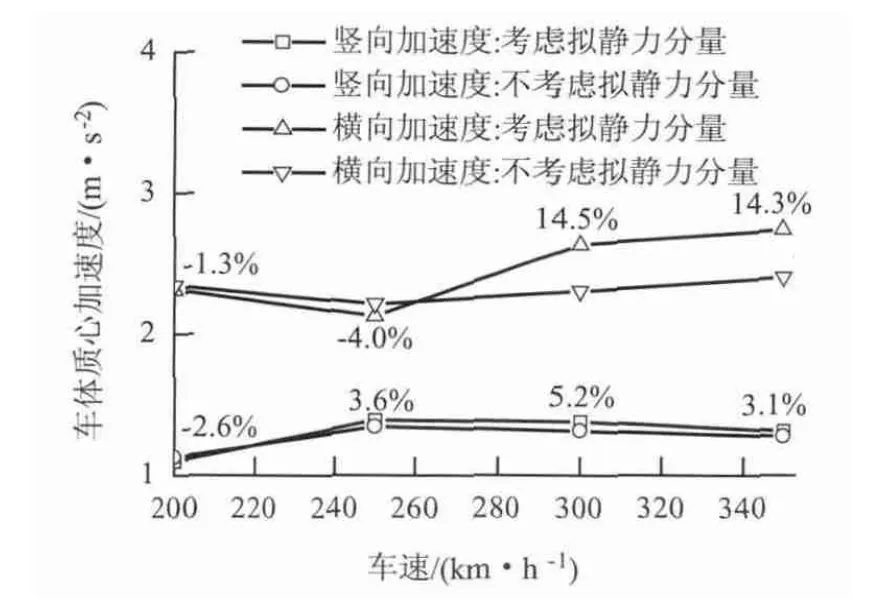
图8 车体加速度幅值随车速的变化Fig.8 Acceleration amplitudes of car body vs. train speed

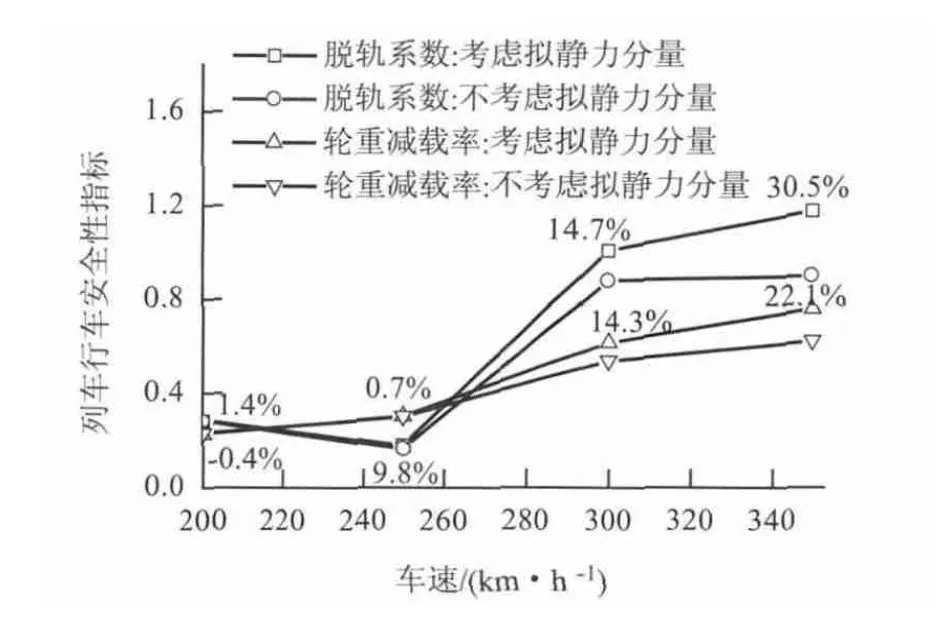
图9 脱轨系数和轮重减载率幅值随车速的变化Fig.9 Derailment coefficient and wheel unloading rate amplitudes vs. train speed

从图8 和图9 可见:(1)考虑结构拟静力分量时，车体的竖向加速度与不考虑时相差不大，最大仅相差5.2%，而横向加速度在高速时相差较大，最大达14.5%;(2)考虑结构拟静力分量时，列车的脱轨系数和轮重减载率明显增大，而且，相对误差随列车速度的提高而增大，最大分别达30.5%和22.2%.

由此可见，不考虑结构拟静力分量可能在列车速度较高时严重低估车辆的动力响应.而高速条件下列车的行车安全性指标常常是评价整列车走行安全性的控制指标，不考虑结构拟静力分量可能造成对地震时桥上列车行车安全性的误判.

4 结 论

本文基于列车-轨道-桥梁动力相互作用理论，考虑路基和桥梁地震力边界条件，分别采用相对运动法和大质量法在相对坐标系和绝对坐标系下处理地震力边界条件，建立了不同坐标系下的列车-轨道-桥梁系统地震响应分析模型，研究了结构拟静力分量对该系统地震响应的影响，得到以下结论:

(1)结构纵向拟静力分量对列车-轨道-桥梁系统的地震响应无影响，竖向拟静力分量仅对列车、轨道、桥梁的竖向动力响应有影响，对列车的行车安全性指标影响不大.当仅研究纵向和竖向地震作用下桥上列车的行车安全性时，可不考虑结构拟静力分量的影响.

(2)结构横向拟静力分量对列车-轨道-桥梁系统动力响应影响最大，将显著增大桥梁与钢轨横向位移、列车脱轨系数、轮重减载率和轮轨横向力.

(3)考虑结构三向拟静力分量时，桥梁、钢轨位移、列车脱轨系数和轮重减载率均显著增大，且脱轨系数和轮重减载率的相对误差随列车速度提高而增大，最大达30.5%和22.2%. 因此，不考虑结构拟静力分量将在列车速度较高时严重低估车辆的动力响应，造成对桥上列车行车安全性的误判.研究三维地震作用下桥上列车的行车安全性时，结构拟静力分量的影响不可忽略，应选择能考虑结构拟静力分量的地震输入方法输入地震激励.

［1］ XIA H，HAN Y，ZHANG N，et al. Dynamic analysis of train-bridge system subjected to non-uniform seismic excitations［J］. Earthquake Engineering ＆ Structural Dynamics，2006，35(12):1563-1579.

［2］ 邓子铭，郭向荣，张志勇. 地震作用对钢桁梁桥车桥系统耦合振动的影响分析［J］. 中南大学学报:自然科学版，2011，42(1):184-191.DENG Ziming，GUO Xiangrong，ZHANG Zhiyong.Coupled vibration of train-bridge system of steel truss bridge with seismic effect［J］. Journal of Central South University:Science and Technology，2011，42(1):184-191.

［3］ 熊建珍，高芒芒，俞翰斌. 天兴洲长江大桥斜拉桥在地震作用下的车-桥耦合振动分析［J］. 中国铁道科学，2006，27(5):54-59.XIONG Jianzhen， GAO Mangmang， YU Hanbin.Vehicle-bridge coupling vibration analysis of cablestayed bridge of Tianxingzhou Yangtze River bridge under earthquakes［J］. China Railway Science，2006，27(5):54-59.

［4］ 韩艳，夏禾，郭薇薇. 斜拉桥在地震与列车荷载同时作用下的动力响应分析［J］. 工程力学，2006，23(1):93-98.HAN Yan，XIA He，GUO Weiwei. Dynamic response of cable-stayed bridge to running trains and earthquakes［J］. Engineering Mechanics，2006，23(1):93-98.

［5］ 王少林，翟婉明. 地震作用下高速列车-线路-桥梁系统动力响应［J］. 西南交通大学学报，2011，46(1):56-62.WANG Shaolin，ZHAI Wanming. Dynamic responses of high-speed train-track-bridge system under seismic excitations［J］. Journal of Southwest Jiaotong University，2011，46(1):56-62.

［6］ ZHANG N，XIA H，De ROECK G. Dynamic analysis of a train-bridge system under multi-support seismic excitations［J］. Journal of Mechanical Science and Technology，2010，24(11):2181-2188.

［7］ YANG Y B，WU Y S. Dynamic stability of trains moving over bridges shaken by earthquakes［J］. Journal of Sound and Vibration，2002，258(1):65-94.

［8］ DU X T，XU Y L，XIA H. Dynamic interaction of bridge-train system under non-uniform seismic ground motion［J］. Earthquake Engineering ＆ Structural Dynamics，2012，41(1):139-157.

［9］ 李小珍. 高速铁路列车-桥梁系统耦合振动理论及应用研究［D］. 成都:西南交通大学土木工程学院，2000.

［10］ 刘德军. 风-列车-线路-桥梁系统耦合振动研究［D］. 成都:西南交通大学土木工程学院，2010.

［11］ 雷虎军，李小珍. 非一致地震激励下列车-轨道-桥梁耦合振动模型［J］. 西南交通大学学报，2013，48(5):803-809.LEI Hujun，LI Xiaozhen. Dynamic model for traintrack-bridge coupling system subjected to non-uniform seismic excitation［J］. Journal of Southwest Jiaotong University，2013，48(5):803-809.

［12］ 翟婉明，夏禾. 列车-轨道-桥梁动力相互作用理论与工程应用［M］. 北京:科学出版社，2011:97-98.

［13］ VERMEULEN J K，JOHNSON K L. Contact of nonspherical bodies transmitting tangential forces［J］.Journal of Applied Mechanics，1964，31:338-340.

［14］ 李小珍，雷虎军. 基于多点激励的刚构-连续组合梁桥行波效应分析［J］. 桥梁建设，2012，42(6):33-38.LI Xiaozhen，LEI Hujun. Analysis of traveling wave effect of hybrid bridge of rigid-frame and continuous girder based on multi-support excitation［J］. Bridge Construction，2012，42(6):33-38.

［15］ 翟婉明. 车辆-轨道耦合动力学［M］. 3 版. 北京:科学出版社，2007:38-78.