基于OFDM 的DF 中继网络能效最优路径选择策略

黄高勇， 方旭明， 陈 煜， 张强锋

(1. 西南交通大学信息编码与传输省重点实验室，四川 成都610031;2. 西南交通大学峨眉校区计算机与通信工程系，四川 峨眉山614202)

过去十多年，许多先进的技术，如OFDMA(orthogonal frequency-division multiple)、MIMO(multiple-input multiple-output)、中继传输等被用于提升无线网络吞吐量和频谱效率. 然而，高吞吐量意味着高能耗，从运营商角度看，高能耗意味着运营成本的上升;从用户终端来看，高能耗意味着能量受限，移动终端无法满足用户的使用需求. 可见，在满足系统资源约束和用户需求前提下，如何降低网络能耗和移动终端能耗已成为未来无线资源分配技术研究新的趋势［1-2］.

将中继技术引入传统的无线蜂窝网，可以扩大网络覆盖范围，提高吞吐量以及达到节能目的［1］.然而，当中继传输与OFDM/OFDMA 技术相结合的时候，无线资源分配问题和路径选择问题(接入站点选择)变得相当复杂.

多跳路径选择方案是影响无线网络资源利用效率的重要因素之一［3］. 对于典型的两跳中继网络，与直传路径相比，中继路径传输需要占用两个时隙传输，因而中继链路有可能降低系统容量［4］，也必然会影响到系统能耗. 因此，如何设计合理有效的路径选择算法仍然是目前许多学者关注的一个研究热点［5-8］.

目前，路径选择问题在各种无线中继网络中得到广泛研究，如Ad hoc 网、无线传感器网络等［6-8］，通常将路径选择问题看成路由问题，并在网络层实现.在无线中继蜂窝网(如802.16j/m 网络)中需要在MAC (media access control)层中实现路径选择算法，因此，这些原有的路径选择算法不能直接被应用到无线中继蜂窝网［5］.

无线中继蜂窝网中典型的路径选择方案主要有以下几种［9-10］:

(1)最小接入距离路径选择算法.该算法只依赖于节点到各个接入点的距离，实现简单;

(2)最大接入链路信道增益路径选择算法.该算法以节点到接入点的信道增益作为判决准则，考虑了路径损耗和阴影衰落的影响;

(3)大尺度衰落最大-最小路径选择算法. 该算法同时考虑了BS (base station)-RS (relay station)和RS-MS (mobile subscriber)链路的链路损耗;

(4)最大调和信道增益路径选择算法.该算法以两跳链路信道增益的调和均值作为路径选择判决准则.

上述算法的目标都是以最大化系统吞吐量为目标.从现有研究成果看，很少有考虑能耗问题的路径选择算法.现有基于OFDMA 无线中继蜂窝网关联能效资源分配的研究大多假定基于传统的路径选择算法，或者简化路径选择问题［11-12］. 因此，对基于能效的路径选择问题的研究具有重要的理论价值和现实意义.

当考虑电路功率消耗、系统功率约束以及用户QoS 需求时，直传路径与中继传输路径选择对系统能效的影响和作用机制仍然不是很清晰，基于此，本文针对单中继三节点DF (decode-and-forward)模式中继传输网络，研究电路功率消耗、用户速率需求、带宽等因素在路径选择时与系统能效之间的关系，提出一种基于等效路径损耗指数的能效最优路径选择判决准则，本文的研究成果可以扩展到多用户多中继OFDMA 蜂窝网络. 研究结果表明，当考虑电路功率消耗的时候，采用中继链路传输并不能保证系统能效一定高于直传链路传输;直传链路与中继链路对发射功率消耗的需求不仅取决于端到端等效信道增益，而且与链路传输速率和带宽有关，并满足本文所提出的最优路径选择判决准则.

1 系统模型与问题描述

考虑图1 所示的单源(S)-单中继(R)-单目的节点(D)的OFDM 中继传输系统(与文献［13］类似).假定数据传输的基本单位为帧(帧周期为Ts)，每帧分为等间隔的2 个时隙，采用固定子载波配对策略，即中继链路传输时第1 跳时隙上发送的数据只能通过第2 跳时隙相同子载波转发.D 可以直接与S 建立直传路径，或通过节点R 建立中继传输路径.

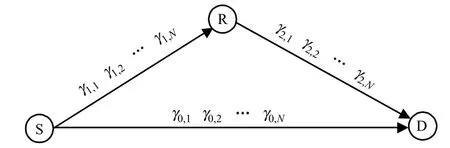
图1 中继传输系统模型Fig.1 System model of the relay transmission system

电路功率消耗包括基带处理功率消耗和射频电路功率消耗.通常假定射频电路功率消耗与发送状态无关;对于低复杂度基带处理系统，基带处理电路功率消耗与射频电路功率消耗相比可以忽略［14］，本文只考虑射频电路功率消耗，包含源节点和中继节点的电路功率消耗总和，且假定平均电路功率消耗为常数.

能效通常定义为单位焦耳能量发送的比特数(bit/J)［15］，直传链路能效定义为

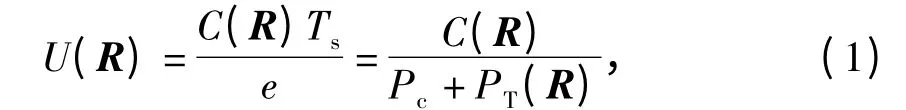
式中:R 为各个子载波上的速率向量;C(R)为所有子载波上的速率和;e 为总能量消耗;Pc为系统电路功率消耗;PT(R)为所有子载波上源节点S 的发射功率和.

能效最大化的目标就是要在一定约束条件下，使得系统能效最大，即

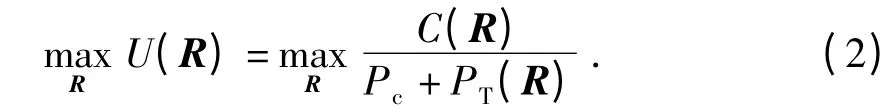
中继链路在子载波n 上的可达速率可以表示为［13］

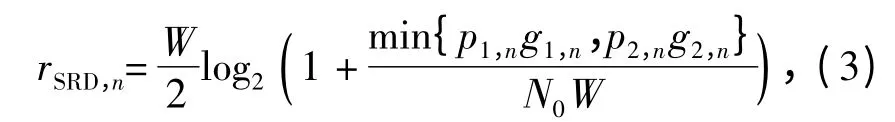
式中:gi，n和pi，n(i=1，2)分别为第i 跳链路子载波n 上的信道功率增益和发射功率;W 为子载波带宽;N0为加性高斯白噪声单边功率谱密度.

由于中继链路传输需要将1 个时隙划分为2 个等时长的子时隙，实现两阶段传输，因此，中继链路端到端可达速率只有直传链路的一半，所以要除以2.

对于本文所考虑的三节点中继传输模型，当系统能效最优时，任意子载波上两跳速率相等. 该结论通过反证法很容易求证:假设系统能效最优时，存在n'，满足r1，n'≠r2，n'.由于任意子载波上的速率取决于两跳速率最小的一跳，可以降低r1，n'和r2，n'中速率较大一跳的功率，使得r1，n'=r2，n'. 此时，系统总发射功率降低，系统能效增大，与原假设矛盾，显然该结论成立. 当系统能效最优时，由于任意子载波n 上两跳链路可达速率满足r1，n=r2，n，易得子载波n 上的端到端等效信道功率增益为

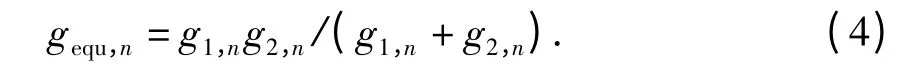
所有子载波上的速率和可以表示为

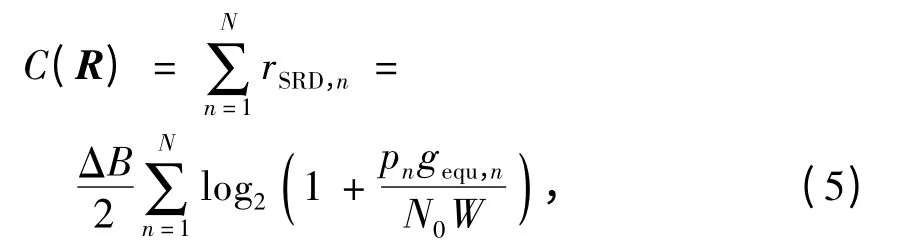
式中:pn为子载波n 上的总发射功率;PT=［p1，p2，…，pN］∈RN+为各子载波上的发射功率变量向量，RN+表示N 维非负实数向量集合.节点S 和R 在子载波n 上的发射功率分别为

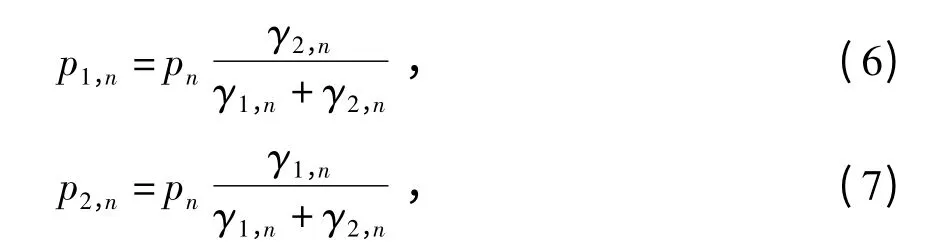
式中:γ1，n=gi，n/(N0W)，表示第i 跳第n 个子载波上的功率归一化信噪比.

所有子载波上的功率和为

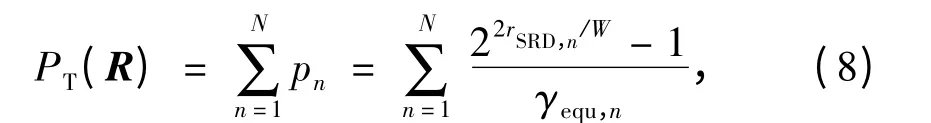
式中:γequ，n=γ1，nγ2，n/(γ1，n+ γ2，n)，表示第i 跳第n 个子载波上的端到端等效功率归一化信噪比.由式(1)能效的定义可知

中继链路的能效可以表示为

2 能效最优路径选择策略

本节针对图1 所示的DF 中继传输系统，提出一种基于等效路径损耗指数的能效最优路径选择策略.该策略的目标是在给定用户速率需求情况下，选择能效最优的路径(直传或中继路径)，该策略适用于任意衰落场景.

由于路径选择时，通常是基于路径损耗和阴影衰落［16］，而频率选择性多信道OFDMA 传输网络各个子载波上的大尺度衰落相等，因此，在基于大尺度衰落路径选择时，可以取所有子载波上平均信道增益作为链路的信道增益. 假定链路总带宽为B，则直传链路和中继链路的可达速率分别表示为

式中:pSD和pSRD分别为直传和中继链路上的总发送功率;gSD和gSRD，equ分别为直传链路信道功率增益和中继链路端到端等效平均信道功率增益.

采用文献［17］式(3.7)经验路径损耗公式换算S-D、S-R 和R-D 链路大尺度衰落值:

式中:fc为中心频率;c =3 ×108m/s 为光速;d 为收、发节点之间的距离，m;α 为路径损耗指数. 将实测直传链路平均信道功率增益gSD，real换算成关于参考距离dref的等效路径损耗:

则等效路径损耗指数αSD，equ可以表示为

式中:ξ=(c/(4πfc))2.同理，可将中继链路等效路径损耗表示为

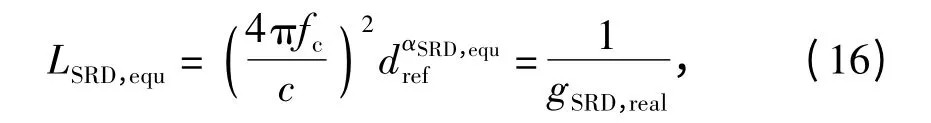
式中:gSRD，real为中继链路端到端等效平均信道功率增益.则中继链路等效路径损耗指数αSRD，equ可以表示为

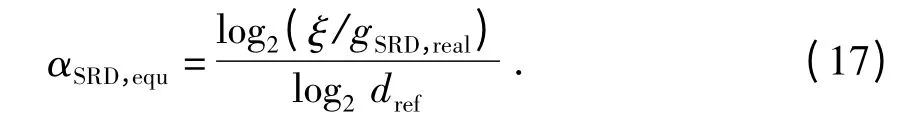
结合式(11)、(12)、(14)和(16)可得中继链路与直传链路发射功率之比为

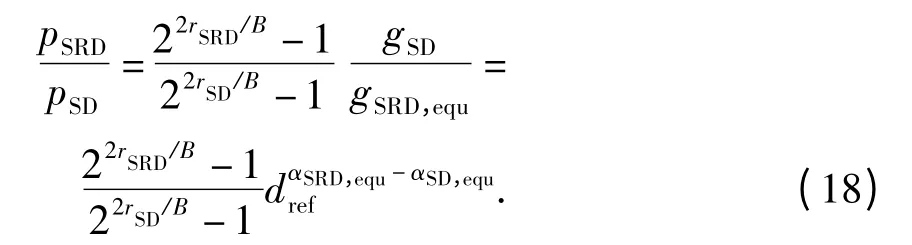
假设用户速率需求为r0，令dref=2，则式(18)可以表示为

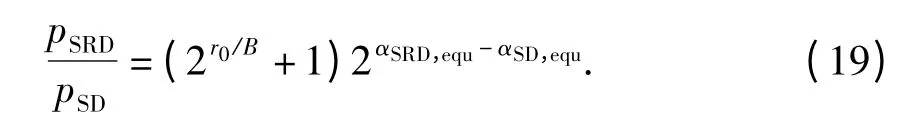
由式(1)和式(10)对直传链路和中继链路能效定义可知，如果链路传输速率和带宽固定，当直传与中继传输链路能效相等时，则需满足

令式(19)等于2，则直传链路和中继链路等效路径损耗指数与用户速率需求和带宽之间满足如下关系:

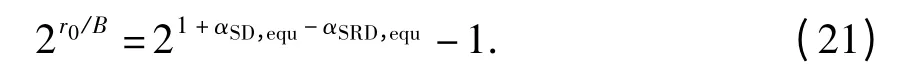
由上述分析可得如下命题:

命题1 对于任意基于DF 模式的三节点中继系统，当系统电路功率消耗PC固定，直传与中继传输路径能效满足如下关系:

(1)当αSD，equ=αSRD，equ时，如果式(21)成立，则r0/B=0，即当r0=0 时，直传与中继路径能效相等，r0＞0 时直传路径能效始终大于中继路径能效.

(2)当αSD，equ＜αSRD，equ时，如果式(21)成立，则r0/B ＜0，即当r0≥0，始终满足pSRD/pSD＞2，直传路径能效始终大于中继路径能效.

(3)当αSD，equ＞αSRD，equ时，直传与中继路径能效满足如下关系:

①当r0/B=log2(21+αSD，equ-αSRD，equ -1)时，直传路径与中继路径能效相等;

②当r0/B ＞log2(21+αSD，equ-αSRD，equ -1)时，直传路径能效大于中继路径能效，从能效最优角度看，选择直传路径传输;

③当r0/B ＜log2(21+αSD，equ-αSRD，equ -1)时，中继路径能效大于直传路径路能效，从能效最优角度看，选择中继路径传输.

3 仿真结果与分析

本节对本文所提出的基于DF 中继能效最优路径选择策略进行仿真分析.

3.1 速率需求、带宽与信道功率增益等因素对能效最优路径选择的影响

为了更深入分析路径选择策略的性能，在不失一般性的前提下，假定信道衰落只考虑路径损耗，S-D、S-R 和R-D 链路的路径损耗模型也采用式(13)的模型，中继节点R 在节点S 和D 连线的中点，系统总带宽B=1 MHz，载波频率fc=2 GHz，帧周期Ts=1 ms，节点S 和D 间的距离固定为600 m.设可达频谱效率SE(spectrum efficiency)为r0/B，表示传输速率r0和带宽B 的比值.图2(a)～图2(f)分析了速率需求、带宽与信道功率增益等因素对能效最优路径选择的影响. 图2(a)为α =3，Pc=100 mW 时，带宽对能效最优路径选择的影响;图2(b)为α =3，B =1 MHz 时，电路功率消耗Pc对能效最优路径选择的影响;图2(c)为Pc=100 mW，B=1 MHz时，路径损耗指数对能效最优路径选择的影响;图2(d)为Pc=100 mW，B =1 MHz 时，可达频谱效率SE 对能效最优路径选择的影响;图2(e)为B =1 MHz 时，直传链路与中继链路能效和信道功率增益随中继位置变化的关系曲线;图2(f)是Pc=100 mW，B=1 MHz 时，发射功率部分的平均能耗随路径损耗指数变化的曲线.

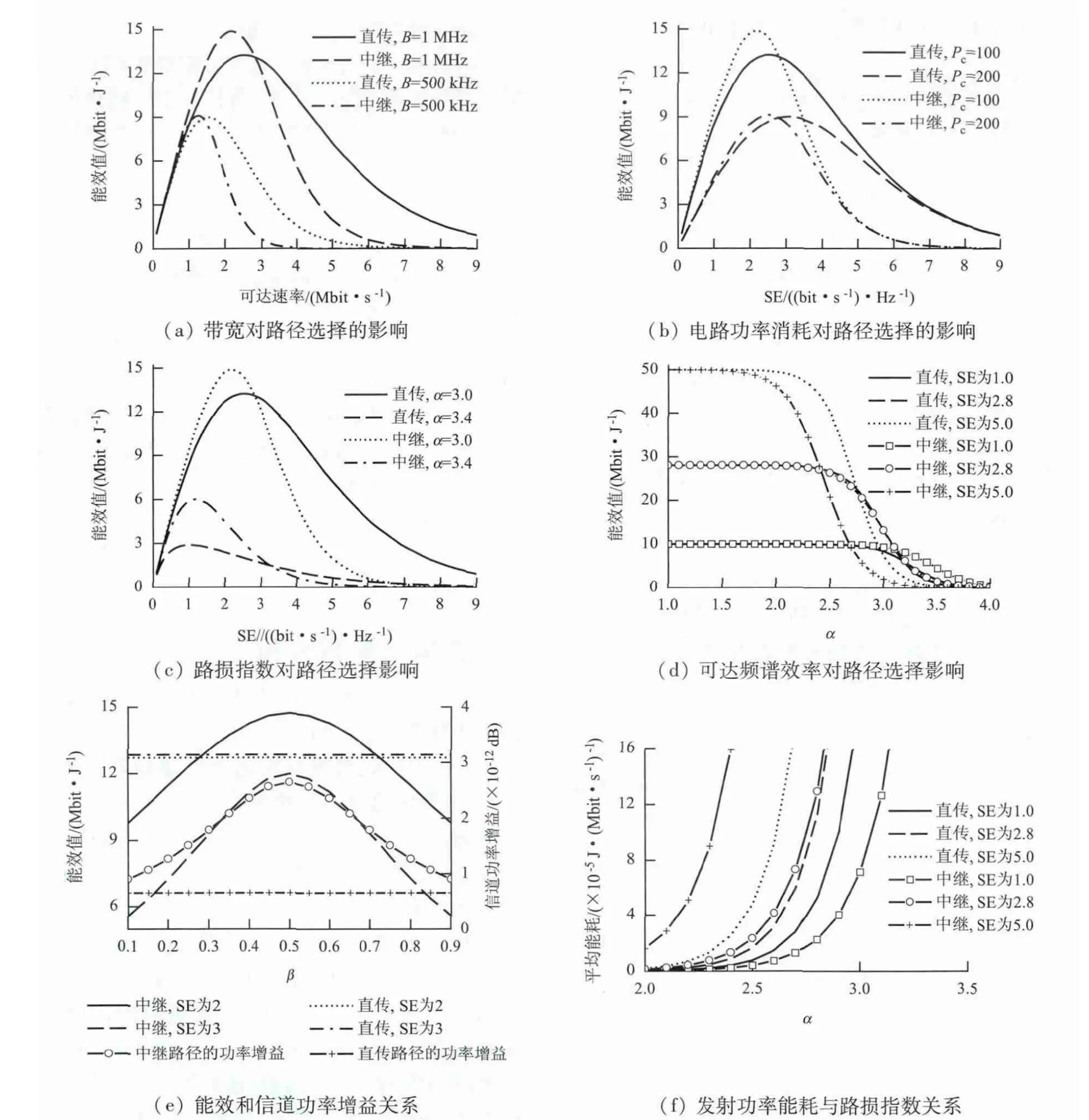
图2 各种参数对链路能效性能的影响Fig.2 Effects of various parameters on system performance

表1 所示为对图2 仿真结果进行的对比分析，由分析结果可见，从能效最大化角度出发，带宽、速率需求、电路功率消耗以及链路信道条件等因素对路径选择都有影响，且满足本文所中命题1 的条件.

3.2 能效最优路径选择方案性能比较

为了衡量本文所提能效最优路径选择方案(proposed scheme)的性能，将本文所提方案与以下4 种典型路径选择算法进行性能对比分析，即:

(1)最小接入距离路径选择算法［9］，选择接入距离最短的接入点作为用户的接入点;

(2)最大接入链路信道增益路径选择算法［10］，选择接入链路信道增益最大的接入点作为用户的接入点;

(3)大尺度衰落最大-最小路径选择算法［9］，对于中继路径，选择BS-RS 和RS-MS 链路大尺度衰落(路径损耗+阴影衰落)最大值作为对比值，再与直传路径的大尺度衰落值比较，选择二者最小的作为用户接入路径;

(4)最大调和信道增益路径选择算法［10］，对于中继路径，以两跳链路调和信道增益作为对比信道增益，并与直传路径信道增益比较，选择信道增益最大的路径作为用户接入路径.

考虑图1 的中继传输场景，假定源节点为基站BS，目的节点为用户MS. MS 与BS 之间可以建立直传路径或通过中继RS 与BS 之间建立中继传输路径.BS-RS 间距离固定为560 m.MS 在BS-RS 连线上，BS-MS 间距离从100 m 增加到850 m. 采用Monte Carlo 仿真方法，仿真结果为10 000 次独立仿真取均值.仿真参数如表2 所示，其中部分仿真参数参考文献［18］.

表1 能效性能分析Tab.1 Performance analysis of the energy efficiency

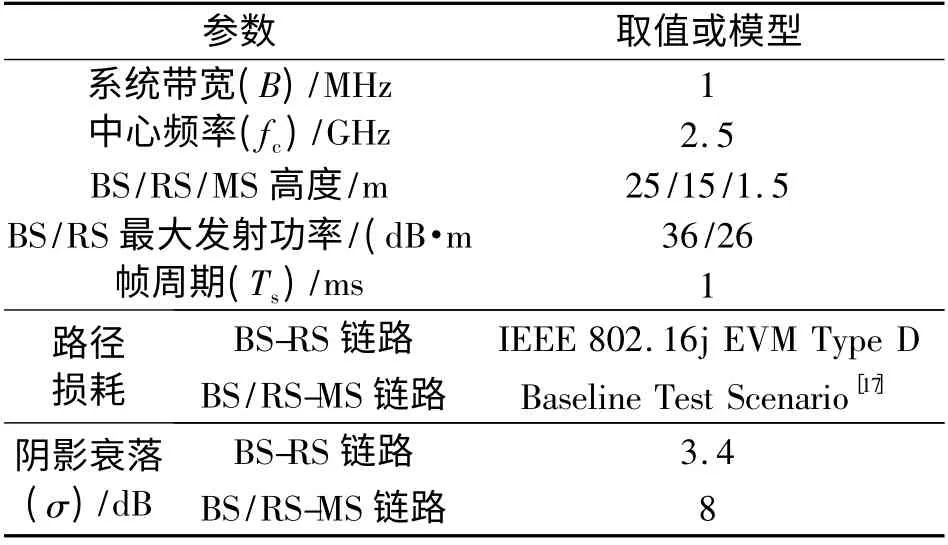
表2 仿真参数Tab.2 Simulation parameters

图3(a)～(c)分别为速率固定为Rmin=5 和6 Mbit/s 时，能效和选择直传路径概率的仿真结果.

(1)从图3(a)和(b)可以看出，本文方案能效性能优于传统的路径选择方案. 例如，BS-MS 距离为610 m，Rmin=5 和6 Mbit/s 时，本文方案的能效比最大调和信道增益路径选择方案分别提高11.8%和40.5%.

(2)从图3(c)可以看出，本文所提方案选择直传路径的概率大于传统的方案，并且速率越大，选择直传路径的概率也越大，而传统的几种路径选择方案选择直传路径的概率与传输速率无关. 例如，BS-MS 距离为610 m，Rmin=5 和6 Mbit/s 时，本文方案选择直传路径的概率分别为36. 7% 和49.6%，而基于等效信道增益路径选择方案选择直传路径的概率始终为4.0%.最小接入距离的路径选择方案由于选择接入点只与节点位置有关，因此，当BS-MS 距离大于BS-RS 连线中点时，完全接入中继节点.

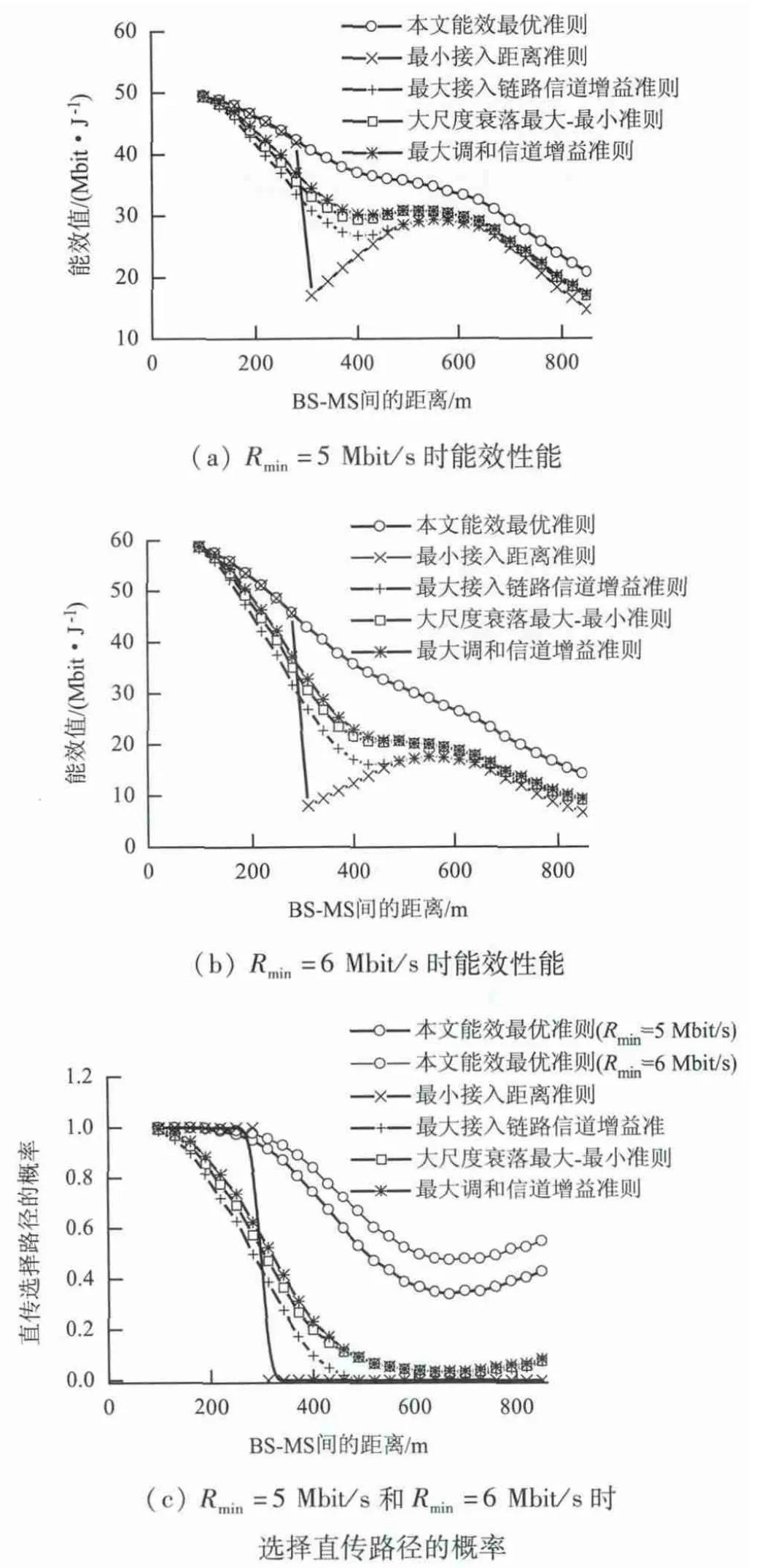
图3 路径选择方案性能比较Fig.3 Performance comparison of the path selection schemes

4 结 论

本文针对DF 中继的单源-单中继-单目的节点传输场景，研究最优能效路径选择问题，提出了一种基于等效路径损耗指数的能效最优路径选择策略.本文所提方案考虑了传输速率、带宽以及信道条件等对路径选择的影响.研究结果表明:

(1)不管是直传路径还是中继路径，路径能效都随带宽的减小而减小，随电路功率消耗的增加而减小.

(2)能效最优路径选择决策结果与电路功率消耗无关，只取决于速率需求和带宽的比值(即可达频谱效率)以及信道条件，且满足命题1 的判决准则.信道条件不变情况下，直传路径与中继路径能效相等点的可达频谱效率不变，能效最优路径只取决于路径传输速率与带宽的比值.

(3)与现有典型路径选择算法相比，本文所提方案可以实现能效最优.

［1］ LI G Y，XU Zhikun，XIONG Cong，et al. Energyefficient wireless communications:tutorial，survey，and open issues［J］. IEEE Wireless Communications，2011，18(6):28-35.

［2］ 黄高勇，方旭明，黄博，等. 基于OFDM 的DF 中继链路能效最优资源分配策略［J］. 西南交通大学学报，2014，49(3):499-506.HUANG Gaoyong，FANG Xuming，HUANG Bo，et al.Scheme for optimal energy-efficient and resource allocation in OFDM-based DF relay link［J］. Journal of Sourthwest Jiaotong University，2014，49(3):499-506.

［3］ IEEE. IEEE 802. 16j-07/079 A new metric for multihop path selection［S］. London:IEEE Press，2007.

［4］ WANG Lichun，SU Wenshan，HUANG J H，et al.Optimal relay location in multi-hop cellular systems［J］.Wireless Networks，2010，16(8):2179-2189.

［5］ WANG S S，LIEN Chanying，LIAO W H，et al. A load-aware spectral-efficient routing metric for path selection in IEEE 802. 16j multi-hop relay networks［J］. Computers and Electrical Engineering，2012，38(4):953-962.

［6］ COUTO D D，AGUAYO D，BICKET J，et al. A highthroughput path metric for multi-hop wireless routing［C］∥ Proceedings of the 9th Annual International Conference on Mobile Computing and Networking. San Diego:IEEE，2003:134-146.

［7］ KOKSAL C E，BALAKRISHNAN H. Quality-aware routing metrics for time-varying wireless mesh networks［J］. IEEE Journal on Selected Areas in Communications，2006，24(11):1984-1994.

［8］ TAM W H，TSENG Y C. Joint multi-channel link layer and multi-path routing design for wireless mesh networks［C］∥ Proceedings of the 26th IEEE International Conference on Computer Communications.Anchorage:IEEE，2007:2081-2089.

［9］ SRENG V，YANIKOMEROGLU H，FALCONER D D.Relay selection strategies in cellular networks with peerto-peer relaying［C］∥Proceedings of the 58th IEEE Vehicular Technology Conference. Orlando: IEEE，2003:1949-1953.

［10］ 黄晓燕，吴凡. 下一代无线网络跨层资源管理［M］.北京:国防工业出版社，2011:55-56.

［11］ JIANG Yun，ZHANG Jianhua，LI Xiaofan，et al.Energy-efficient resource optimization for relay-aided uplink OFDMA systems［C］∥Proceedings of the 75th IEEE Vehicular Technology Conference. Yokohama:IEEE，2012:1-5.

［12］ ZHANG Jianhua，JIANG Yun，LI Xiaofan. Energyefficient resource allocation in multiuser relay-based OFDMA networks［J］. Concurrency and Computation:Practice and Experience，2013，25(9):1113-1125.

［13］ LI Yong，WANG Wenbo，KONG Jia，et al. Subcarrier pairing for amplify-and-forward and decode-and-forward OFDM relay links［J］. IEEE Communications Letters，2009，13(4):209-211.

［14］ SUN Can， YANG Chenyang. Energy efficiency analysis of one-way and two-way relay systems［J］.EURASIP Journal on Wireless Communications and Networking，2012，46:1-18.

［15］ MIAO Guowang，HIMAYAT N，LI GEOFFREY Y.Energy-efficient link adaptation in frequency-selective channels［J］. IEEE Transactions on Communications，2010，58(2):545-554.

［16］ LI Qian，HU Qingyang，YI Qian，et al. Intracell cooperation and resource allocation in a heterogeneous network with relays［J］. IEEE Transactions on Vehicular Technology，2013，62(4):1770-1784.

［17］ ANDREWS J G， GHOSH A， MUHAMED R.Fundamentals of WiMAX:understanding broadband wireless networking［M］. ［S. l.］:Pearson Education Inc，2007:101.

［18］ IEEE 802.16 Broadband Wireless Access Working Group. IEEE 802.16m-08/004r5—2008 IEEE 802.16m evaluation methodology document (EMD)［S］. New York:IEEE，2009.