基于一阶统计量的子空间旋转不变解相干算法

李 磊，李国林

（海军航空工程学院，山东 烟台 264001）

0 引言

在现代战争中，精确制导武器已经成为信息化局部战争中物理杀伤的主要手段，这就需要引信探测系统具备高精度、快速目标空间定向能力，实时精确的估计目标的二维波达方向（direction of arrival，DOA）。同时，由于敌方转发式干扰或多径效应，探测空间存在大量相干或强相关信源，使得常规空间谱估计算法估计性能下降甚至失效，因此，研究相干信源和低信噪比背景下精确快速的二维解相干算法显得尤为重要。

近年来，阵列信号处理在DOA 估计领域涌现出了许多子空间类算法［1-3］，但相干或强相关信源会导致阵元接收数据的协方差矩阵亏秩，信号子空间向噪声子空间扩散，算法估计错误。针对相干信源DOA 估计问题，常用处理方式为空间平滑及其改进算法。文献［4］提出一种基于四阶累积量和时间平滑的联合处理算法，扩展了阵列的自由度，且具有抑制高斯色噪声的能力。文献［5］基于共轭循环平稳信号特点，提出了一种虚拟阵列空间平滑算法，提高了DOA 估计的精度和稳健性。另一种常用的解相干算法是矩阵重构类算法，文献［6］研究了一种基于矩阵重构的波束形成自适应算法，利用Toeplitz特性恢复矩阵的秩实现信源完全解相干。文献［7］提出了一种改进的Hermitian型矩阵构造方法，有效降低了信源相关度，但上述算法均基于数据的二阶统计特性，需要在时域上进行大快拍数据累计及相关运算，计算量大。殷勤业等提出了DOA 矩阵算法［8］，具有计算量小，参数自动配对等优点，同时针对相干信源入射背景提出空域平滑DOA 矩阵算法，但空域平滑处理过程增加了算法的计算复杂度。单次快拍类算法［9］通过一次快拍数据构造解相干矩阵，以一次快拍携带信息代替整体数据的统计特性，虽然计算量小，但在信噪比较低时会导致DOA估计精度大幅下降，鲁棒性差，无法满足武器探测系统的估计精度指标。针对以上问题，本文提出基于一阶统计量的子空间旋转不变（ESPRIT）解相干算法。

1 信号接收模型

假设N 个中心波长为λ 且均值不为零的远场窄带信号源si（t），i=0，1，…，N 入射到图1所示双平行线阵系统。阵列由两个各向同性且均匀分布的线阵子阵构成，其中子阵X 共2 M 个阵元，阵元编号分别为-（M-1），…，0，…，M ，子阵Y 共2 M-1个阵元，编号分别为-（M-1），…，0，…，M-1。两子阵间距为D，阵元间距为d。

图1 阵列模型Fig.1 Array model

图中，αi、βi 和γi分别表示第i个信源si（t）分别与x、y 和z 轴之间的夹角，则由几何关系可知cos2αi+cos2βi+cos2γi=1成立，即αi、βi 和γi中只有两个独立元素，此处定义αi和βi 分别为入射信源sk（t）的方位角和俯仰角，表述信源的二维波达方向。假设噪声为零均值加性高斯白噪声，阵元间噪声彼此独立，且与信号不相关。

以子阵X 编号为0的阵元作为参考阵元，则子阵X 第i个阵元的输出信号可表示为：

式中，

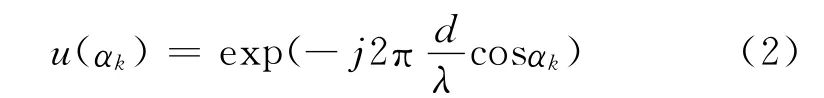
同理，子阵Y 第i个阵元的输出信号可表示为：

式中，nxi（t）和nyi（t）分别表示子阵X 和子阵Y 第i个阵元的零均值加性高斯白噪声，满足

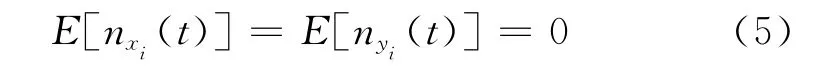
2 基于矩阵重构的解相干算法

常规子空间类谱估计算法都需要进行时域快拍累积（快拍次数大多数通常在数百次以上），然后计算阵列接收数据协方差矩阵，需要进行大量自相关及互相关运算，并且协方差矩阵在相干入射信源背景会导致亏秩现象［10］。本节利用信号一阶统计特性构造伪协方差矩阵，无需复杂的相关运算，计算量小，且保证重构的协方差矩阵在相干源背景下不会出现亏秩，从而实现解相干。

将子阵X 进一步分为两个子阵，前2 M-1个阵元（编号为-（M-1），…，0，…，M-1）组成子阵X1，后2 M-1个阵元（编号-（M-2），…，0，…，M ）组成子阵X2。则子阵的信号输出矢量分别表示为：

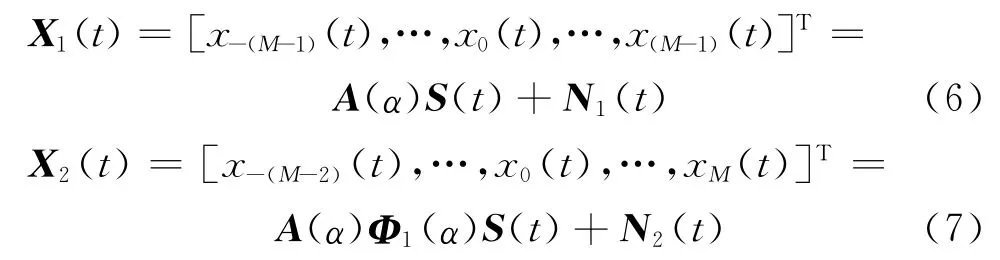
子阵Y 的信号输出矢量表示为：

式中，A（α）是（2 M-1）×N 维阵列流型矩阵。

子阵X 和子阵Y 接收数据的一阶矩定义为：

其中，

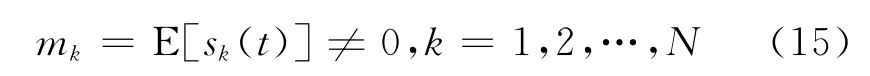
表示入射信号的均值。利用子阵X1接收数据的一阶 矩mxi，i=- （M -1），…，0，…，M -1 构 造Toeplitz形式的伪协方差矩阵Q1

则易推得

第M 行至第2 M-1行

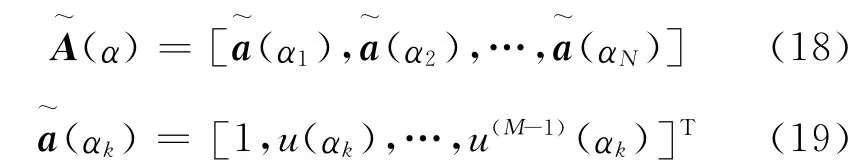
可以看出，矩阵Rm为对角阵，则Q1的秩只与信源个数相同，而与信源之间的相关性无关，即可实现完全解相干。另一方面，由式（16）可知本文构造的伪协方差矩阵能够有效滤除噪声分量，保证了算法在低信噪比下的估计性能。

同理，分别利用子阵X2和子阵Y 接收数据的一阶矩构造伪协方差矩阵Q2和Q3

利用上述三个具有旋转不变关系的伪协方差矩阵，进一步构造3 M×M 维的扩展协方差矩阵Q

对矩阵Q 进行奇异值分解（Q=UΣVH），由奇异值分解的意义可知，若矩阵Q 的秩为N ，则矩阵U 的前N 列组成Q 的列空间的标 准正交基［11］。因此，奇异值分解得到的信号子空间可表示为US=U（：，1：N），而奇异值分解的信号子空间与阵列流型张成的信号子空间相同，即满足如下关系：

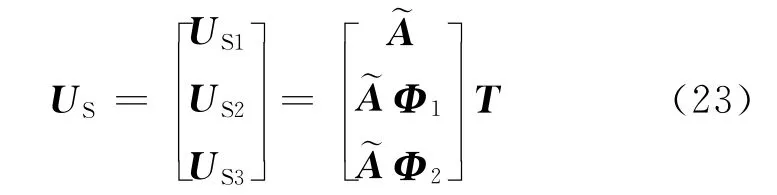
其中，US1=US（1：M，：），US2=US（M +1：2 M，：），US3=US（2 M+1：3 M，：），则信号子空间之间满足下列关系式

由式（26）及式（27）求最小二乘解，可得

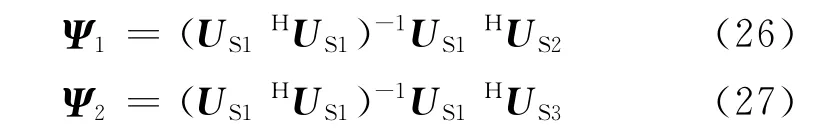
由Φ1和Φ2的形式可知，Φ1只和方位角α 有关，Φ2只和俯仰角β有关。分别对Ψ1和Ψ2进行特征分解，则Ψ1和Ψ2的特征值组成的对角阵与Φ1和Φ2相同，结合式（2）和式（4）即可得到信源入射的二维DOA。

理论上，对Ψ1和Ψ2进行特征分解可得到同样的特征向量矩阵T，但实际运算中两次特征分解是独立进行的，导致两次特征分解的特征向量矩阵T1和T2的排序可能不同，但同一信号在两次特征分解中的特征向量强相关，可构造式（28）所示排序矩阵R，依据矩阵R 每列的最大值来调整β 的顺序，即可实现二维角度参数匹配。

下面给出本文算法的具体步骤：

步骤1 获取子阵接收数据X（t）和Y（t）；

步骤2 根据式（13）和式（14）计算子阵X 和子阵Y 接收数据的一阶距mxi和myi；

步骤3 根据式（16）、式（20）和式（21）构造伪协方差矩阵Q1、Q2和Q3；

步骤4 根据式（22）构造扩展协方差矩阵Q，对其奇异值分解并取左奇异向量矩阵U 的前N 列为信号子空间US；

步骤5将US按式（23）划分3个子空间，并按式（26）和式（27）求得Ψ1和Ψ2；

步骤6将Ψ1和Ψ2进行特征值分解，得到Φ1和Φ2。根据式（2）和式（4）的求得αi和βi，并按照式（28）进行配对。

由算法步骤可知，本文算法基于阵列接收数据的一阶统计量，步骤1-步骤3对数据预处理过程不存在复乘运算，算法的复乘运算主要集中在后三个实现步骤，约为O（M2N+29 M3）。常规平滑类算法需要进行数据平滑处理，则设定平滑次数为K ，子阵阵元数为M ，快拍次数为L。空域平滑DOA 矩 阵 法［8］需 要 的 复 乘 次 数 约 为O（M2NL +3 M3），由上文可知，基于二阶统计量的DOA 算法所需时域快拍累计次数多为数百次以上，则本文算法比空域平滑DOA 矩阵法的计算量低。另外，传统二维ESPRIT 平滑算法［12］所需复乘次数约为O（8 M2NL+65 M3），则本文算法的计算复杂度较之下降更为明显。

3 数值仿真

为验证算法的正确性和有效性，设计如下matlab仿真。考虑DOA 矩阵类算法［8］在分辨力和计算复杂度方面相较其他二维DOA 估计算法的优势，将本文算法与DOA 矩阵法及空域平滑DOA 矩阵法进行对比，分析算法优势和局限性。

仿真1：相干信源的二维DOA 估计。假设三个均值非零远场窄带相干信源分别从方向（30°，80°），（55°，35°）和（85°，60°）入 射 至 图1 所 示 阵列，设定阵元参数M=9，信噪比SNR=10dB，阵列噪声为零均值加性高斯白噪声。为避免阵列产生测向模糊，设定阵元间距d=λ／2，快拍数均为50次，每种算法分别进行100 次的Monte-Carlo统计仿真，其估计星座图如图2所示。

图2 相干信源下算法DOA 估计星座图Fig.2 DOA estimation constellation of coherent signal sources

由图2（a）可知，本文算法可实现相关信源的完全解相干，这是由于算法构造的伪协方差矩阵的秩仅与信源个数有关，保证了算法的二维解相干能力。图2（b）所示空域平滑DOA 矩阵法通过空域平滑处理也能实现二维DOA 估计，但其解相干能力是以空域平滑所产生的计算量为代价，且其估计结果散布较大，估计性能不及本文算法。分析其原因，一方面，本文算法在构造伪协方差矩阵的过程中有效滤除了噪声分量，受噪声影响较小。另一方面，本文算法基于阵列数据的一阶统计特性，受快拍次数影响较小。而DOA 矩阵法建立在阵列数据的二阶统计特性，对数据长度的要求很高，只有在时域快拍累积非常大时才能达到较高的估计性能。图2（c）所示常规DOA 矩阵法由于协方差矩阵降秩，DOA 估计已经失效。同时必须看到，本文算法利用信号一阶矩特性直接构造伪协方差矩阵，避免了常规子空间类算法的复杂相关运算，运算量小，更适用于武器引信探测系统的应用背景。

仿真2：信噪比对算法估计性能的影响。考虑阵列和信号模型不变，快拍次数不变，使信噪比从0 dB到20dB 区间以1dB 的步长递增，每个信噪比下分别进行100次独立Monte-Carlo统计仿真，考察本文算法和空域平滑DOA 矩阵法的均方根误差（root-mean-square error，RMSE）和分辨成功概率随SNR 变 化 关 系。DOA 估 计 的RMSE 定 义［11］为：

式中，（αk，βk）为实际值，（^αk，^βk）为估计值。

图3（a）为RMSE 随信噪比变化曲线。随着信噪比的增大，两种算法的DOA 估计的RMSE 都逐渐减小，且本文算法RMSE 始终比空域平滑DOA矩阵法小，尤其当信噪比较低时。分析其原因，当阵列噪声为零均值高斯白噪声时，本文构造的伪协方差矩阵能够有效滤除噪声分量。虽然空域平滑DOA 矩阵法也进行了相应的去噪处理，但由于快拍次数较小，其去噪能力受到一定限制。当SNR=0 dB时，空域平滑DOA 矩阵法的三个信源RMSE 分别约为1.8、1.9 和2.1，而本文算法三个信源RMSE相对较小，分别约为0.6、1和1.3，估计精度更高。

图3（b）为分辨成功概率随信噪比变化曲线。设定信号DOA 估计的RMSE小于1时视为分辨成功。可以看出，两种算法对每个信源的DOA 估计分辨概率随信噪比的增大而提高，且本文算法优于空域平滑DOA 矩阵法，与之前的理论分析保持一致。

图3 估计性能随信噪比变化曲线Fig.3 Performance curves vs.SNR

仿真3：快拍次数对估计性能的影响。考虑阵列和信号模型不变，设定信噪比SNR=10dB，快拍数从50到1000以50为步长递增，每个快拍数下分别进行100 次独立Monte-Carlo统计仿真，得到本文算法和空域平滑DOA 矩阵法的RMSE随快拍次数的变化关系如图4所示。显然，随着快拍数的增加，两种算法的3个信源DOA 估计的RMSE 都逐渐减小，且本文算法DOA 估计的RMSE始终比相同快拍数时的空域平滑DOA 矩阵法小，与上文分析一致。在快拍数为50次时，本文算法将三个相干信源的估计误差均控制在1以内，更符合少快拍数下引信探测系统对目标二维方位估计精度的需求。

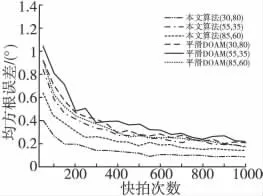
图4 RMSE随快拍次数变化曲线Fig.4 RMSE curves vs.snapshots

4 结论

本文提出基于一阶统计量的二维ESPRIT 解相干算法。算法利用阵元接收数据的一阶统计量构造三个Toeplitz形式的伪协方差矩阵，实现了相干信源的解相干。然后通过构造扩展协方差矩阵并对其进行一次奇异值分解即实现了相干信源的二维DOA 估计。仿真结果表明：该算法在低信噪比和少快拍数下具有比空域平滑DOA 矩阵法更高的估计性能，且避免了传统算法对大量时域快拍累计的协方差矩阵的处理过程，计算复杂度低，实时性高。

［1］蒋柏峰，吕晓德.一种基于导向矢量变换的DOA 估计预处理方法［J］.电子与信息学报，2012，34（7）：1552-1557.

［2］宋爱民，李堰，刘剑，等.非圆信号多级维纳滤波DOA估计求根算法［J］.电子科技大学学报，2013，42（1）：53-57.

［3］Mendoza Montoya F，Covarrubias R D H，Lopez-Miranda C A.DOA estimation in mobile communication system usingsubspace tracking methods［J］.IEEE Latin America Transactions，2008，6（2）：123-129.

［4］景小荣，隋伟伟，周围.基于四阶累积量和时间平滑的相干信号DOA 估计［J］.系统工程与电子技术，2012，34（4）：789-795.

［5］张聪，胡谋法，卢焕章.基于虚拟阵列空间平滑的相干信号DOA 估计［J］.电子学报，2010，38（4）：929-933.

［6］Gao Jian-yong，Gao Yong.The adaptive beamforming algorithm for coherent sources non-uniform linear array based on improved Toeplitz approximation［J］.Journal of Astronautics，2007，28（6）：1715-1718.

［7］韩勇，乔晓林，金铭，等.空间相关信号源高分辨处理的Toep-MUSIC 改进算法［J］.系统工程与电子技术，2009，31（7）：1544-1547.

［8］殷勤业，邹理和，Newwcomb W R.一种高分辨率二维信号参量估计方法-波达方向矩阵法［J］.通信学报，1991，12（4）：1-7.

［9］洪升，万显荣，易建新，等.基于单次快拍的双基地MIMO雷达多目标角度估计方法［J］.电子与信息学报，2013，35（5）：1149-1156.

［10］张贤达.矩阵分析与应用［M］.北京：清华大学出版社，2009.

［11］王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京：清华大学出版社，2009.

［12］董轶，吴云韬，廖桂生.一种二维到达方向估计的ESPRIT 新方法［J］.西安电子科大学报，2003，30（5）：569-575.